Rでの方法はこちらを参照。
データはRのpsychパッケージに含まれるものを利用するので、作成方法は下部に記載する。 (追記: 2021/12/06) データの内容についてはこちらを参照。
Mplusのコード
TITLE:
Exploratory Factor Analysis by Mplus, using IPIP-NEO data.
DATA:
FILE = "bfi.dat";
VARIABLE:
NAMES = A1-A5 C1-C5 E1-E5 N1-N5 gender education age;
USEVARIABLES = A1-A5 C1-C5 E1-E5 N1-N5;
MISSING = .;
ANALYSIS:
TYPE = EFA 3 6;
ESTIMATOR = ML;
ROTATION = oblimin;
PARALLEL = 50;
PLOT:
TYPE = plot2;
OUTPUT:
residual;
DATA:
データを置いた場所を指定する。日本語のフォルダ内に入れない方が良い。データのエンコードはUTF-8にしておこう。
VARIABLE:
今回使うのはA1からN5の25個のデータ。
ANALYSIS:
EFAとはExploratory Factor Analysisの省略。
3 6となっているのは、3因子モデルから6因子モデルを検討するという意味。
推定法はML、回転はオブリミオン回転を指定している。回転を指定しない場合のデフォルト値はオブリミオン回転なので、指定はしなくてもよい。
PARALLELは平行分析のサンプリング数。この数を大きくすると、計算が長くなるのでほどほどにしておこう。Mplusのマニュアルでは50回と例示されてある*1が、 Finch & Bolin(2017)では1000という例示がある(p.177)のでマシンパワーがあれば大きい数字でもよいのだろう。
PLOT:
スクリープロットの出力を指定。
まず因子数を決めることから始める。 とはいっても、このデータの妥当な因子数はよくわからない。
ガットマン基準
RESULTS FOR EXPLORATORY FACTOR ANALYSIS
EIGENVALUES FOR SAMPLE CORRELATION MATRIX
1 2 3 4 5
________ ________ ________ ________ ________
4.729 2.581 2.019 1.468 0.979
固有値1を超えるのは4因子モデルである。5因子モデルになると0.979と1を切るため、固有値を1以上とするガットマン基準からは4因子モデルが提案される。
モデル改善の検定
モデルのフィッティングを見てみよう。
SUMMARY OF MODEL FIT INFORMATION
Degrees of
Model Chi-Square Freedom P-Value
3-factor 2794.270 133 0.0000
4-factor 1376.733 116 0.0000
5-factor 903.210 100 0.0000
6-factor 649.008 85 0.0000
Degrees of
Models Compared Chi-Square Freedom P-Value
3-factor against 4-factor 1417.537 17 0.0000
4-factor against 5-factor 473.523 16 0.0000
5-factor against 6-factor 254.203 15 0.0000
Models Comparedのところをみると、モデルが改善されたかがわかる。改善しなくなったところで打ち止めをするのが通常である。具体的にはカイ二乗検定のP値をみる。例えば、6因子モデルのP値が0.360とかになっていると、モデルが改善していないとして、一つ前の5因子モデルを採用する。
ただ、実際には6因子モデルも0.000なので、5→6因子モデルにすることによってフィッティングは改善していることになっている。
追記(2021/12/05)
Bengt O. Muthenは下記の記述があった。
http://www.statmodel.com/discussion/messages/8/26371.html?1539133417
このような矛盾したメッセージは、実際のデータでもよく起こる。なぜなら、データは、ある数の因子を持つ完全な因子モデルを表していない可能性があるからである。例えば、m個の因子があっても、いくつかの残差相関がある場合がある。この場合、カイ二乗はmよりも多くの因子を持つべきだとでますが、これは本当のモデルではない。これは、いくつかの因子が2つの有意な負荷量しか持たないことでよく現れる。残差相関が存在するかどうかを確認するために、修正指数を見てほしい。一般的には、平行分析の方がこの問題に強いかもしれないが、これが徹底的に研究されているかどうかはわからない。そしてもちろん、どのような解決策がトピックの理論とどのように関連しているかを確認する必要がある。
MAP
Velicer(1976)のMinimum Average Partial(MAP)はMplusのオプションには含まれないようだ*2。
MAPの値を出せるのは、服部先生の「忍者はっとりくん」、清水先生のHAD、RのpsychパッケージにあるVSS()関数のようだ。MAPのデータが必要な時には別のプログラムが必要である。
BIC
| Model | BIC |
|---|---|
| 3-factor | 184190.261 |
| 4-factor | 182907.658 |
| 5-factor | 182561.134 |
| 6-factor | 182425.992 |
BICは小さいほうがフィッティングがよいとされている。微妙に数値が現象して行っているが、6因子が最も小さく、値も劇的に改善しているとも言いづらいため、あまり参考にはならなさそうである。
ちなみに、BICはプロマックス回転では出力されない。
スクリープロット
下の図はスクリープロットと平行分析の図である。
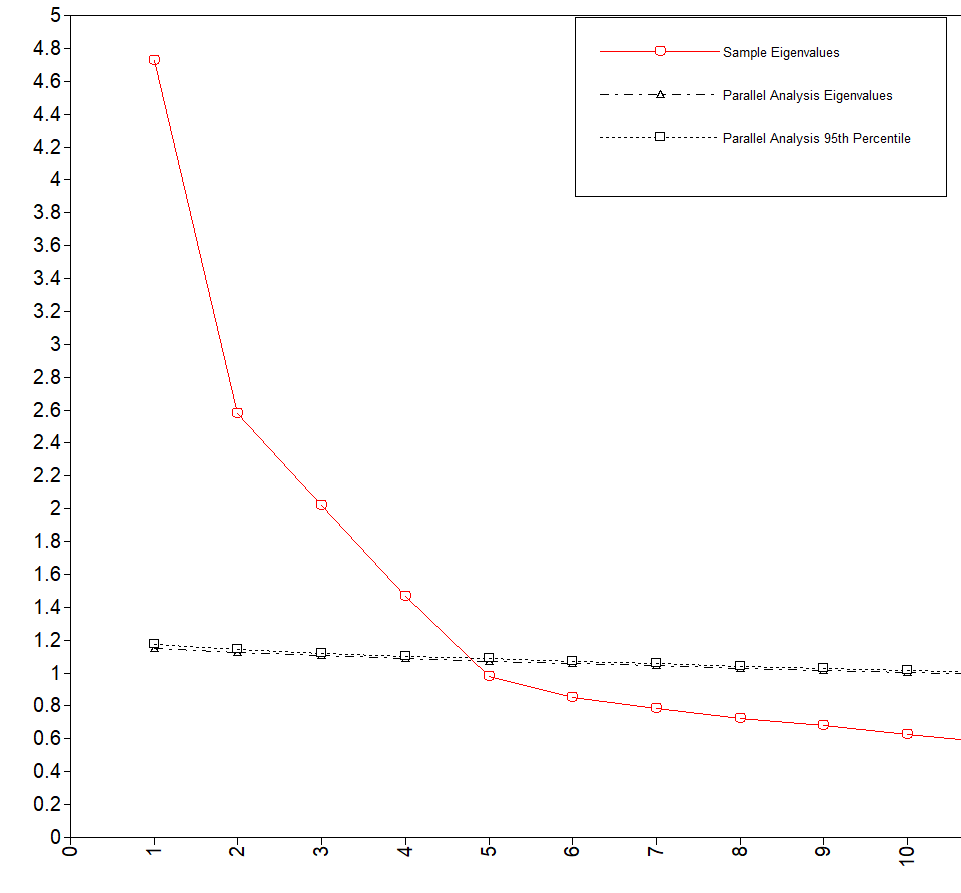
スクリープロットは推移がなだらかになる前までの数値を採用するので、4因子モデルが良さそうである。
平行分析
黒色の斜め横点線より上側の因子数を採用する方法である。清水先生のブログでちゃんと説明されているのでま詳しい解説はそちらで。
このデータの場合は4因子モデルが支持されている。
結論
基準を総合すると4因子モデルがよさそうである。
このデータはNEOなのでもともとは5因子モデルのデータであったはずなのだが、統計量は4因子モデルを指示している。
データ作成 追記: 2021/12/06
Rで作成する。
データ呼び出し
library("psych")
data(bfi)
df1 <- bfi
実数型に変数型を変更
df1$A1<-as.numeric(df1$A1) df1$A2<-as.numeric(df1$A2) df1$A3<-as.numeric(df1$A3) df1$A4<-as.numeric(df1$A4) df1$A5<-as.numeric(df1$A5) df1$C1<-as.numeric(df1$C1) df1$C2<-as.numeric(df1$C2) df1$C3<-as.numeric(df1$C3) df1$C4<-as.numeric(df1$C4) df1$C5<-as.numeric(df1$C5) df1$E1<-as.numeric(df1$E1) df1$E2<-as.numeric(df1$E2) df1$E3<-as.numeric(df1$E3) df1$E4<-as.numeric(df1$E4) df1$E5<-as.numeric(df1$E5) df1$N1<-as.numeric(df1$N1) df1$N2<-as.numeric(df1$N2) df1$N3<-as.numeric(df1$N3) df1$N4<-as.numeric(df1$N4) df1$N5<-as.numeric(df1$N5) df1$O1<-as.numeric(df1$O1) df1$O1<-as.numeric(df1$gender) df1$O1<-as.numeric(df1$education) df1$O1<-as.numeric(df1$age)
この作業はMplusAutomation()がnumericでないとうけつけないため。
Mplusデータの書き出し
library(MplusAutomation) variable.names(df1) # 変数名を書き出し prepareMplusData(df1, filename="bfi.dat", overwrite=T)
*1:http://www.statmodel.com/download/usersguide/Chapter16.pdf
*2:No, Mplus doesn't do that MAP test. posted by Bengt O. Muthen, http://www.statmodel.com/discussion/messages/8/20916.html?1429281795
