新しい質問紙・尺度(主に心理系)を作る際や翻訳をする際に求められることが多い内的整合性・内的妥当性の尺度で比較的有名である。今回は、サンプルサイズの計算方法についてである。
Bonettによる計算式を紹介しよう。
Bonett DG., 2002, "Sample size requirements for testing and estimating coefficient alpha." J Educ Behav Stat. ;27(4):335–340. https://journals.sagepub.com/doi/10.3102/10769986027004335
クロンバッハのαの比較2つの値を比較する実験にも使われる。どちらの尺度・どちらの構成の方が値が高いか(=内的整合性が取れているか)といった使い方だ。その場合は、サンプルサイズはかなり小さくてよい。尺度を作成する先に、どの項目をいれたらよいかという判断材料のになる。
一方で、よく使われるのは、単独でα係数を使用する研究である。その際に必要とされるサンプルサイズの計算式は下記のものである。
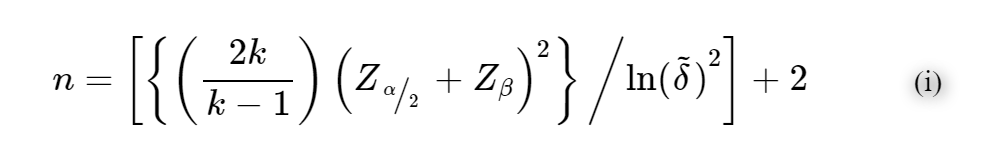

...第一種の過誤(偽陽性)
...第二種の過誤(偽陰性)
...項目数/評価者数
...クロンバッハのαの帰無仮説の値
...クロンバッハのαの期待値
Zは標準正規分布、lnは自然対数である。 下記の値を入れてみよう。項目数は15であり、クロンバッハのαの期待値は0.7と設定している。Zの値は手計算でする際には、標準正規分布表を参照する。
...0.05
...0.1
...15
...0.0
...0.7
...1.96
...1.282
計算式に入れると下記のようになる。
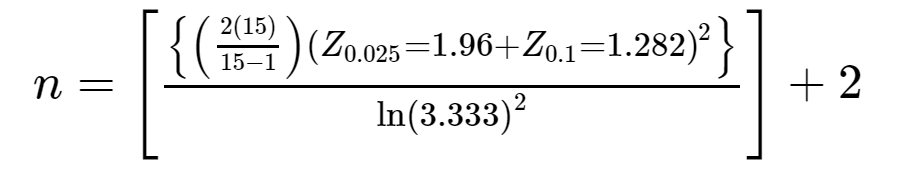
結果は約18ということが判明した。
帰無仮説の値であるCA0を0にすると比較的少数のサンプルサイズで良いことがわかる。
クロンバッハのαの値は相場感的には0.5以下だと低いとされているので、CA0=0.5にするとサンプルサイズはやや大きくなる(Bujang et al. 2018)。
クロンバッハのαのサンプルサイズにいての下記のレビューは無料で全文閲覧できる。 www.ncbi.nlm.nih.gov
計算方法が統計パッケージでは用意されていないようなのでExcelシートで作成した。
クロンバッハのαのサンプルサイズの推定計算シート