カーネギーメロン大学のCosma Shalizi氏の「R二乗値は何の役にも立たない」関連。
バージニア大学図書館のクレイ・フォード氏によるシミュレーションをみてみよう。
2015年10月16日(木)、不信感を抱いた学生がRedditに投稿した。私の統計学の教授が、R二乗の値は本質的に役に立たないという暴言を吐いたのですが、これには何か真実があるのだろうか? 少なくともRedditの他の統計に関する投稿と比較すると、かなりの注目を集めた。
この学生の統計学の教授は、カーネギーメロン大学のCosma Shalizi氏であることが判明しました。Shaliziは、彼の授業の講義資料を無料で公開しているので、彼が一体何について「暴言」を吐いたのかを見ることができる。それは、彼の第10講のノートの3.2節から始まっている。
R2乗は回帰出力によく現れる統計量であることを忘れたのだろうか?これは0から1までの値で、通常、回帰モデルが説明する応答の変動のパーセンテージを要約していると解釈される。したがって、R2乗が0.65というのは、モデルが従属変数の変動の約65%を説明することを意味する。このロジックを考えると、我々は回帰モデルが高いR2乗を持つことを好む。しかし、Shaliziは、説得力のある議論によってこの論理に異議を唱えている。
Rでは、通常、モデル・オブジェクトのsummary関数を呼び出して、R2乗を求める。以下はシミュレーションデータを使った簡単な例である。
x <- 1:20 # 独立変数 set.seed(1) # 再現性のため y <- 2 + 0.5*x + rnorm(20,0,3) # 従属変数; x の関数で、ランダムな誤差。 mod <- lm(y~x) # 単純な線形回帰 summary(mod)$r.squared # R2乗の値だけを要求する。
結果
[1] 0.6026682
R2乗は、フィット値の偏差の2乗の合計をオリジナル値の偏差の2乗の合計で割った値で表される。
このようにモデルオブジェクトを使って直接計算することができる。
f <- mod$fitted.values # モデルから適合値(または予測値)を取り出す mss <- sum((f - mean(f))^2) # 適合値の偏差の二乗の和 tss <- sum((y - mean(y))^2) # 元値の偏差の二乗の総和 mss/tss # R2乗
結果
[1] 0.6026682
では、R二乗に関するShaliziの発言をいくつか取り上げ、Rでのシミュレーションで実証してみよう。
1. R2乗は適合度を測るものではない。
モデルが完全に正しい場合、恣意的に低くなることがある。σ2を大きくすることで、単純な線形回帰モデルのすべての仮定があらゆる点で正しくても、R2乗を0に近づけることができる。
σ2とは?線形回帰を実行するとき、我々はモデルが従属変数をほとんど予測すると仮定する。「ほぼ」と「正確」の差は、平均0、我々がσ2と呼ぶ分散を持つ正規分布からの抽選であると仮定される。
Shaliziの発言は、実証するのがとても簡単である。ここでは、(1)単純な線形回帰の仮定(独立した観測値、一定の分散を持つ正規分布の誤差)を満たすデータを生成し、(2)単純な線形モデルをデータに適合させ、(3)R2乗を報告する関数を作成する。簡便にするためパラメータはシグマのみであることに注意してほしい。次に、この関数をσの値が増加する系列に「適用」して、結果をプロットする。
r2.0 <- function(sig){
x <- seq(1,10,length.out = 100) # 我々の予測変数
y <- 2 + 1.2*x + rnorm(100,0,sd = sig) # 応答; x といくつかのランダムノイズの関数である。
summary(lm(y ~ x))$r.squared # R2 乗の値を表示する。
}
sigmas <- seq(0.5,20,length.out = 20)
rout <- sapply(sigmas, r2.0) # 一連のシグマ値に対して関数を適用する。
plot(rout ~ sigmas, type="b")

確かに、モデルがあらゆる点で完全に正しいにもかかわらず、シグマが大きくなるとR2乗は大きく減少します。
2. R2乗は、モデルが完全に間違っている場合、任意に1に近づけることができる。
繰り返しになるが、R2乗は適合度を測るものではない、ということである。ここでは、Shaliziの講義10のノートの別のセクションにあるコードを使って、非線形データを生成してみよう。
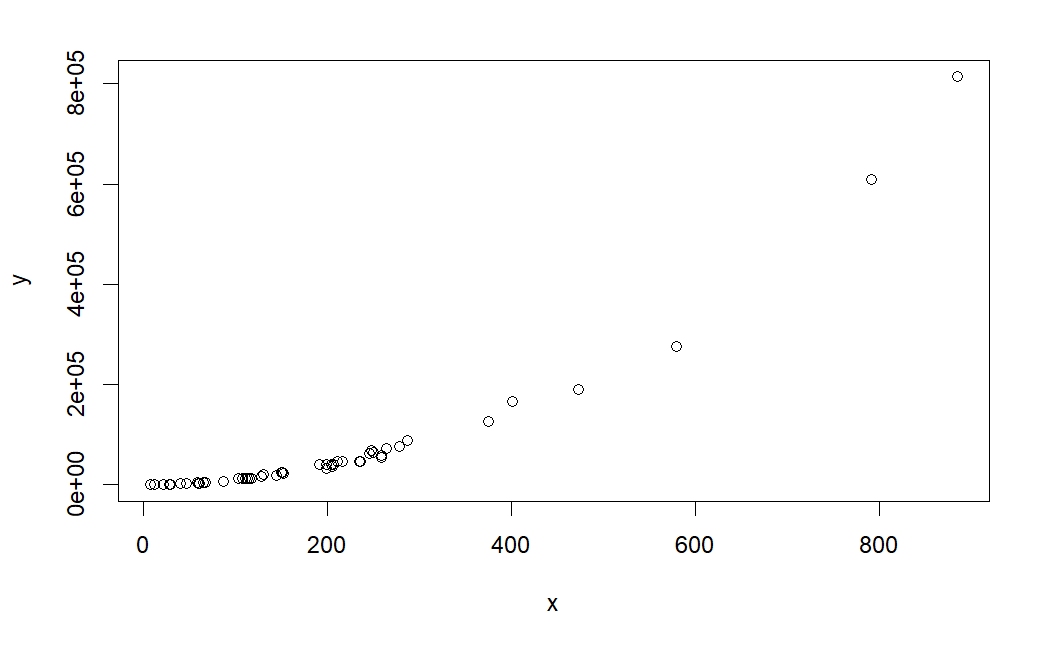
set.seed(1) x <- rexp(50,rate=0.005) # 予測器は指数分布からのデータ y <- (x-1)^2 * runif(50, min=0.8, max=1.2) # 非線形データ生成 plot(x,y) # 明らかに非線型であることを確認する
ここで、R2乗を確認する。
summary(lm(y ~ x))$r.squared
[1] 0.8485146
およそ0.85と非常に高い値であるが、このモデルは完全に間違っている。この例でモデルの「goodness」を正当化するためにR2乗を使うのは間違いであろう。願わくば、まずデータをプロットして、この場合の単純な線形回帰が不適切であることを認識してほしいである。
3.R2乗は、σ2が全く同じで、係数が変わらなくても、予測誤差について何も言及できない。
R2乗はXの範囲を変えるだけで、0から1の間のどこにでもなる。予測誤差の指標としては、平均二乗誤差(MSE)を使う方がよいだろう。
MSEは基本的に、フィットしたy値から観測されたy値を引いたものを2乗し、それを合計し、観測回数で割ったものである。
まず、単純な線形回帰の仮定をすべて満たすデータを生成し、yをxに回帰してR2乗とMSEの両方を評価することで、この記述を実証してみよう。
x <- seq(1,10,length.out = 100) set.seed(1) y <- 2 + 1.2*x + rnorm(100,0,sd = 0.9) mod1 <- lm(y ~ x) summary(mod1)$r.squared
[1] 0.9383379
sum((fitted(mod1) - y)^2)/100 # 平均二乗誤差
[1] 0.6468052
今度は上のコードを繰り返すが、今度はxの範囲を変えてほしい。
x <- seq(1,2,length.out = 100) # xの新しい範囲 set.seed(1) y <- 2 + 1.2*x + rnorm(100,0,sd = 0.9) mod1 <- lm(y ~ x) summary(mod1)$r.squared
[1] 0.1502448
sum((fitted(mod1) - y)^2)/100 # 平均二乗誤差
[1] 0.6468052
R2乗は0.94から0.15に低下しましたが、MSEは変わらなかった。言い換えれば、予測能力は両方のデータセットで同じですが、R2乗を見ると、最初の例の方が何らかの形でより予測能力の高いモデルを持っていると思わせるのである。
4.R2乗は、変換されていないYと変換されたYのモデル間、またはYの異なる変換間の比較はできない。
それでは、変換が有効なデータを生成して検証してみよう。以下のRコードは、以前の取り組みと非常によく似ているが、今度はy変数を指数関数化することに注意してほしい。
x <- seq(1,2,length.out = 100) set.seed(1) y <- exp(-2 - 0.09*x + rnorm(100,0,sd = 2.5)) summary(lm(y ~ x))$r.squared
[1] 0.003281718
plot(lm(y ~ x), which=3)
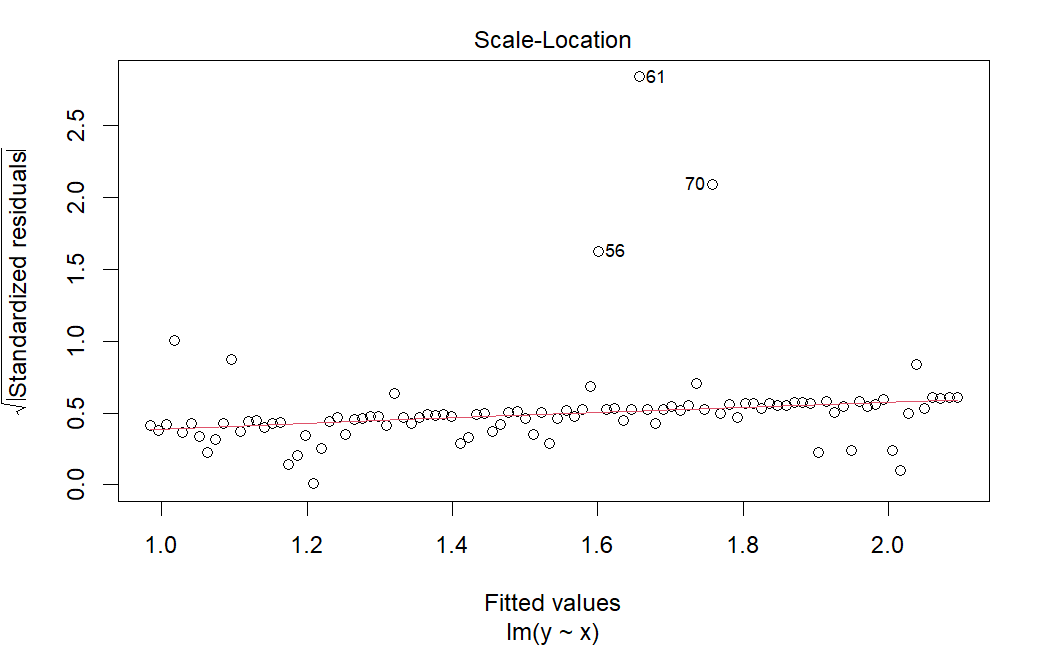
R2乗は非常に低く、残差対適合プロットは外れ値や一定でない分散を明らかにする。この問題を解決するには、データを対数変換することが一般的である。それを試して、何が起こるか見てみよう。
plot(lm(log(y)~x),which = 3)
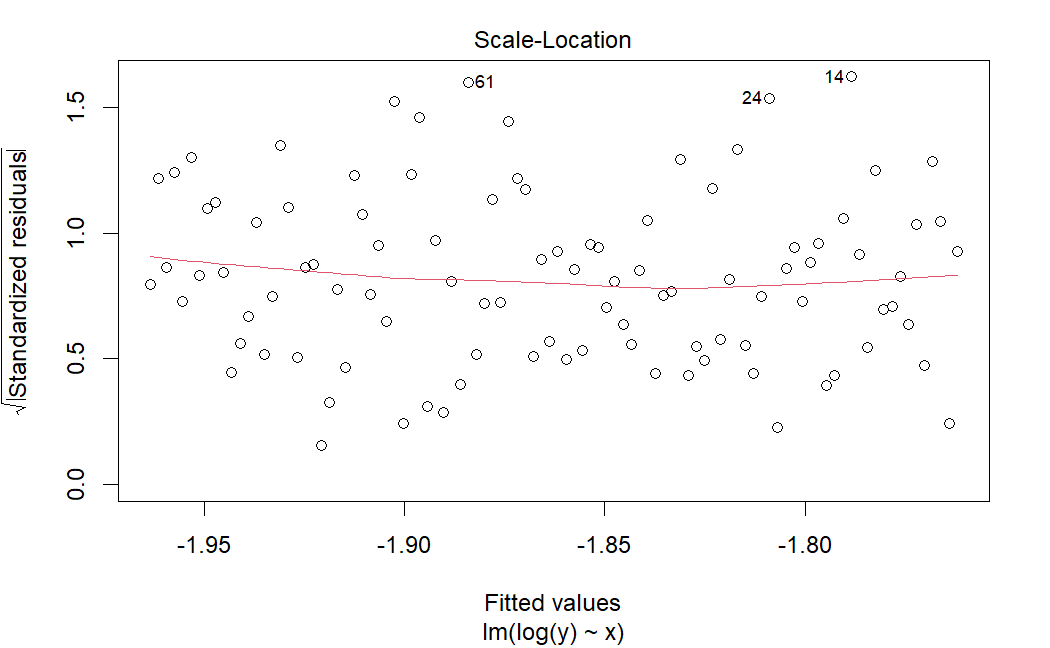
診断プロットはかなり良くなっているようだ。分散が一定であるという我々の仮定は満たされているように見る。しかし、R2乗を見てほしい。
summary(lm(log(y)~x))$r.squared
[1] 0.0006921086
さらに低くなっている! これは極端な例で、いつもこのようになるわけではない。実際、対数変換を行うと、通常はR2乗が増加する。しかし、先ほど示したように、よりよく満たされた仮定が必ずしも高いR2乗をもたらすとは限らない。したがって、R2乗はモデル間で比較することができなのである。
5.R2乗は回帰によって「説明される分散の割合」であると言うのは非常に一般的である。しかし、XをYに回帰させたら、全く同じR2乗が得られる。このこと自体、高いR2乗はある変数を別の変数で説明することについては何も語っていないことを示すのに十分であろう。
これは、最も実証しやすい。
x <- seq(1,10,length.out = 100) y <- 2 + 1.2*x + rnorm(100,0,sd = 2) summary(lm(y ~ x))$r.squared
[1] 0.7065779
summary(lm(x ~ y))$r.squared
[1] 0.7065779
xがyを説明するのか、yがxを説明するのか? 「説明する」という言葉は「原因」という言葉を避けているのだろうか? このような2変数の単純なシナリオでは、R2乗は単にxとyの相関の2乗である。
all.equal(cor(x,y)^2, summary(lm(x ~ y))$r.squared, summary(lm(y ~ x))$r.squared)
[1] TRUE
この場合、R2乗の代わりに相関を使えばいいのでは? しかし、相関は線形関係を要約するもので、データには適していないかもしれない。このような場合にも、データをプロットすることが強く推奨される。
改めて確認しよう。
- R2乗は適合度を測るものではない。
- R2乗は予測誤差を測定しない。
- R2乗は、変換された回答を使用してモデルを比較することはできない。
- R2乗は、ある変数が他の変数をどのように説明するかを測定しない。
Shalizi氏は講義ノートでさらに多くの理由を述べている。そして、Adjusted R-squaredはこれらの問題のどれにも対処していないことに留意すべきである。
では、R2乗を使う理由はあるのだろうか? Shaliziは「ない」と言っている(「私は、それが全く役に立ったという状況を見つけたことがない」)。間違いなく、一部の統計学者やRedditorは反対するでしょう。あなたの見解がどうであれ、データ分析にR2乗を使うのであれば、それがあなたの考えていることを伝えているかどうか、再確認するのが賢明だろう。