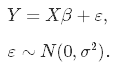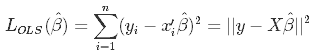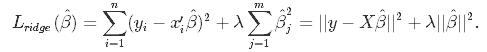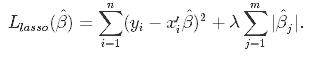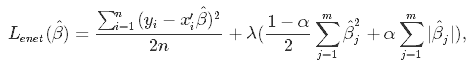献本御礼：セイックラ、アーンキル 『開かれた対話と未来 今この瞬間に他者を思いやる』

開かれた対話と未来 今この瞬間に他者を思いやる

監訳者の斎藤環さんにいただきました。350ページを超える本なのでぱっと見は読むに時間がかかりそうですが、とても読みやすい感じの内容です。
最初に30ページ弱の監訳者「はじめに」があって、本書の位置づけを確認できます。巻末には対話実践のガイドライン(オープンダイアローグ・ネットワーク・ジャパンによるもの)もあり実践的な仕上がりです。

この本には章によって難易度が異なるとのこと。
入門的な内容や全体的な解説となると斎藤さんが書かれている本がいくつかありますが、セイックラの著書でというと下記のものが翻訳されています。

オープンダイアローグ

まえがきを読んで、科学的な効果の検証について少し考えてみて、このエントリに書いていましたが、ボリュームがそこそこ大きくなったので、別エントリにまとめようと思います。

ides.hatenablog.com

２値カテゴリカル因子分析と潜在クラス分析のシミュレーション, その２

前回のエントリ、２値のカテゴリカル因子分析と潜在クラス分析の結果の差異で因子分析と潜在クラス分析のグループ分けの違いを分析した。

今回は以前のエントリで使用した児童向けウェクスラー式知能検査（Wechsler Intelligence Scale for Children; WISC)のデータを用いて、シミュレーションをしてみたい。今回は連続変数(打ち切り)が元データである。

データの読み込み

library(foreign)
data <- read.spss("wiscsem.sav", to.data.frame=TRUE)
d1 <- data[3:13] ## 因子分析に使用するのは3～13列目，連続変数のためのデータ
library(OneR)
d2 <- bin(d1, nbins = 2, labels = c(1,2))
library(dplyr)
d3 <- d2 %>% mutate_if(is.factor, as.integer) # 整数型への変換

d1が連続変数のデータ、d2が2値のfactor型データ、d3が２値の整数型のデータである。
因子数の2であったため、今回も2因子として分析する。

2値の因子分析を行う。

library("psych")
library("GPArotation")
fa2.ca <- fa(r = d3, nfactors = 2, fm = "minres", 
                   rotate = "oblimin", scores=TRUE, cor="tet")
print(fa2.ca, digits = 3)

	因子1	因子２
info	0.978	-0.085
comp	0.351	0.438
arith	0.453	0.335
simil	0.647	0.214
vocab	0.785	0.033
digit	0.353	-0.023
pictcomp	0.080	0.679
parang	-0.082	0.444
block	0.087	0.537
object	-0.101	0.731
coding	-0.141	0.231

参考までに連続変数の因子分析もしておこう。

fa2.n <- fa(r = d1, nfactors = 2, fm = "minres", 
                  rotate = "oblimin", scores=TRUE, cor="cor")
print(fa2.n, digits = 3)

結果は以下のようになる。

	因子1	因子２
info	0.831	-0.075
comp	0.502	0.315
arith	0.604	-0.031
simil	0.562	0.225
vocab	0.743	0.029
digit	0.487	-0.128
pictcomp	0.063	0.587
parang	0.095	0.382
block	0.057	0.616
object	-0.088	0.656
coding	0.101	-0.021

やはり連続変数で分けた方が明確な結果が得られる。
前半は言語性IQ、後半は動作性IQと言われるものである。

特徴としては、符号(coding)はどちらの因子にも含まれていないという点であろうか。

さて、これを潜在クラス分析で2クラスにしてみるとどのようになるだろうか。

Rで潜在クラス分析

library(poLCA)
f <- cbind(info,comp,arith,simil,vocab,digit,
                 pictcomp,parang,block,object,coding)~1 
                  #fomulaの設定。潜在クラス分析に入れる変数を選ぶ
lca2 <- poLCA(f, d2, nclass=2,maxiter=3000, nrep=100) #5クラスモデル

結果は以下のようになる。

	クラス1	クラス2
info	0.0465	0.5041
comp	0.3329	0.8528
arith	0.0781	0.4652
simil	0.2218	0.8748
vocab	0.2061	0.8176
digit	0.3686	0.5790
pictcomp	0.2982	0.7680
parang	0.5594	0.7648
block	0.3430	0.6872
object	0.2692	0.6506
coding	0.6412	0.6003

クラス1はIQでストが悪かったタイプ、クラス２はIQテストが良かったタイプというように分かれた。符号(coding)はどちらの割合も高い。

今回もかなり異なったグループ分けとなった。
因子分析は言語性と動作性という2つIQ概念の違いが出てきた。因子分析は項目、つまり概念のグループ分けだからだ。
一方で、潜在クラス分析はIQが低いタイプとIQが高いタイプという２分割がされた。潜在クラス分析はケース、つまり、人の持つ性質のグループ分けだからだ。

潜在クラス分析の適正なクラス数

潜在クラス分析の結果が身もふたもない結果だったので、潜在クラス分析の適正なクラス数の推定しておこう。詳しくは以前のエントリを参照してほしい。

データの出力

write.csv(d3, file = "WISC.csv", row.names=FALSE, fileEncoding = "UTF-8")

Mplusのコマンドも一応書いておこう。

  TITLE:
    Categorical Factor Analysis vs. Latent class Analysis, using WISC Data
    
  DATA:
    FILE = WISC.csv;

  VARIABLE:
    NAMES = info comp arith simil vocab digit pictcomp parang block object coding;
    USEVARIABLES = info comp arith simil vocab digit pictcomp parang block object coding;
    CATEGORICAL = info comp arith simil vocab digit pictcomp parang block object coding;
    CLASSES = c (2);

  ANALYSIS:
    TYPE = MIXTURE;
    
  OUTPUT:
    TECH14;

BICとBLRTとP-vlaueは次のようになった。

	BIC	BLRT Approximate P-Value
2class	2456.137	0.0000
3class	2475.115	0.0000
4class	2509.824	0.1923

指標間の差はなく3クラスが提案されている。
Mplusで出力された3クラスの結果は以下。

	Class1	Class2	Class3
所属割合	0.371	0.217	0.411
info	0.612	0.000	0.061
comp	0.850	0.693	0.235
arith	0.478	0.191	0.078
simil	0.910	0.400	0.216
vocab	0.926	0.213	0.221
digit	0.628	0.253	0.429
pictcomp	0.758	0.669	0.192
parang	0.756	0.788	0.480
block	0.659	0.717	0.228
object	0.613	0.776	0.096
coding	0.572	0.807	0.567

クラス１はすべての能力が高いタイプ。
クラス２は動作性IQが高いタイプだ。ただComprehension(理解力)のみ高い。

クラス３は言語性IＱのみ高いタイプであれば、きれいな結果なのだが、少し変わったクラスが作成れている。Digit Span、Paragraph Arrangement、codingが高く、Information、Arithmetic、Object Assemblyが低いというクラスだ。IQ検査を数多く実施している臨床家であれば、こういう児童がいることに心当たりがあるのかもしれないが、僕は臨床家でもなければIQについても詳しくないので、さっぱりわからない。

WISCを利用した臨床研究は「Aさんはこのようなタイプの能力が高かった／低かった」という論じ方が多い。個別例であれば特に問題はないが、ある程度の人数を根拠に傾向を論じるのであれば、因子分析を用いて妥当性が確保するWISCとの齟齬が生じる。臨床研究は人(ケース)単位で考えるので、潜在クラス分析の推定の方が理論と統計学の手技がフィットするからだ。

WISCやWAISといった知的機能検査というのは、概念(各種検査)を用いたグループ分けで妥当性が確保されている。しかし、そういった知的機能検査を、人を単位とした臨床のパターンについて語るのは望ましくないはずなのだが、臨床心理学のIQの議論では当たり前のようにされている。そのあたりの事情は臨床家は勉強することからは外れているので知らなくても仕方ないのだが、計量の学者からわかりやすく伝える努力が必要になってくるだろう。

２値のカテゴリカル因子分析と潜在クラス分析の結果の差異

２値のカテゴリカル因子分析と２値の潜在クラス分析の結果どのように違うのかをシミュレーションしてみたい。因子分析も潜在クラス分析もグループ分けをする手技である。しかし、両者はグループの分け方が異なる。因子分析が変数の近さでグループを作るのに対して、潜在クラス分析はケースのパターンでグループを作成する。

今回使うデータはいつも使っているIPIP-NEOである。データの性質は以前に書いているのでこちらを参照してほしい。

データの作成

library("psych")
data(bfi) # IPIP-MEO のデータ
d1 <- bfi[1:25] # 因子分析に使用するのは１～25列目
library(OneR)
d2 <- bin(d1, nbins = 2, labels = c(1,2)) #２分位
library(dplyr)
d3 <- d2 %>% mutate_if(is.factor, as.integer) # 整数型への変換

d1が順序変数のデータ、d2が2値のfactor型データ、d3が２値の整数型のデータである。

因子数の決定

もともと５因子のデータだが、因子数の決定についても見ていこう。

平行分析

fa.parallel(d1)
fa.parallel(d3)

MAP情報量

R_map<-vss(d3)
print(R_map,digits =4)
R_mapC<-vss(d1)
print(R_mapC,digits =4)

順序変数では平行分析は6因子、MAP情報量は5因子を提案をしている。 2値データでは平行分析は6因子、MAP情報量は2因子を提案をしている。 MAP情報量は順序変数や連続変数では比較的良い因子数の提案をしてくれるが、2値では正確に推定するのはと難しいのかもしれない。このデータでは、平行分析の方が良い提案をしているように思える。

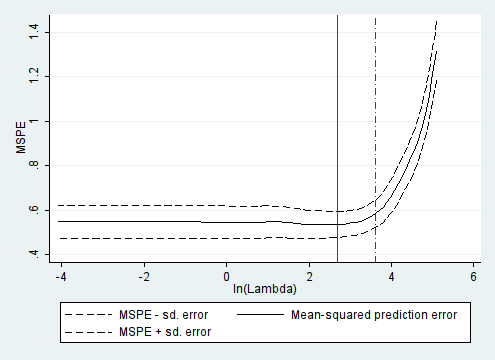
クラス数の決定

潜在クラス分析のクラス数はどうだろうか。今回はBICとBLRT(Bootstrap Likelihood Ratio Test)を利用する。潜在クラス分析はRでもできるが、BLRTはMplusでしかできないので、Mplusで計算する。

データ下記のように出力する。Mplusは変数名はコマンドの中に書き込むので、write.csvで出力する場合は、一行目を消す。write.tableコマンドを使うと変数名は出力されないが、コンマではなくスペース区切りなので、エディタなどで置換をすることになる。

どちらでも手間のかからない方法でやってほしい。変数名を出力しないオプションがあるのかもしれない(いや、きっとあるだろう)が、調べてみてもわからなかったので、今後の課題として積み残しておこうと思う。

write.csv(d3, file = "IPIP-NEO.csv", row.names=FALSE, fileEncoding = "UTF-8")

Mplusの潜在クラスのコマンド(.inpファイル)は下記のように書く。クラス数はc()の中の数字を変えるだけである。クラス数を変える場合はその都度.inpファイルを作り実行する。

  TITLE:
    Categorical Factor Analysis vs. Latent class Analysis
  DATA:
    FILE = IPIP-NEO.csv;

  VARIABLE:
    NAMES = A1-A5 C1-C5 E1-E5 N1-N5 O1-O5;
    USEVARIABLES = A1-A5 C1-C5 E1-E5 N1-N5 O1-O5;
    CATEGORICAL = A1-A5 C1-C5 E1-E5 N1-N5 O1-O5;
    CLASSES = c (2);

  ANALYSIS:
    TYPE = MIXTURE;
  OUTPUT:
    TECH14;

BLRTのp-valueは10クラスモデルまで計算してみた。Approximate P-Valueはすべて0.000であり、モデル数を増やせば増やすだけモデルは改善していると判断されている。BICも次第に小さくなっているので、クラスを増やせば増やすほど、モデルは改善している判断されている。このデータは収束しないようだ。残念ながらクラス数の決定はできなかった。理由は後ほど、クラスを詳しく見ていくとわかると思う。

class	Approximate P-Value	BIC
2	0.0000	64643.860
3	0.0000	63269.515
4	0.0000	62850.673
5	0.0000	62555.632
6	0.0000	62486.493
7	0.0000	62407.838
8	0.0000	62402.985
9	0.0000	62397.464
10	0.0000	62414.749

Rで因子分析

R戻る。 5因子の因子分析をRで行う。

library("psych")
library("GPArotation")
fa5 <- fa(r = d3, nfactors = 5, fm = "minres", rotate = "oblimin", scores=TRUE)
print(fa5, digits = 3)

Rでの潜在クラス分析

潜在クラス分析も5クラスで分析する。BLRTを使わないならば、Rで十分なので、Rで実行する。poLCAパッケージを利用する。注意するのはデータをfactor型にしないとプログラムが走らないことだ。最初にd2でfactor型のデータを作っているので、それを利用する。ちなみに、因子分析はinteger型(整数型)でないとプログラムが走らない。言われてみれば、確かにその通りなのだが、各パッケージはこのあたりは厳格なので、気をつけよう。

library(poLCA)
f <- cbind(A1,A2,A3,A4,A5,C1,C2,C3,C4,C5,E1,E2,E3,E4,E5,
           N1,N2,N3,N4,N5,O1,O2,O3,O4,O5)~1
           #fomulaの設定。潜在クラス分析に入れる変数を選ぶ
lca5 <- poLCA(f, d2, nclass=5,maxiter=3000, nrep=100) #5クラスモデル

因子分析の結果

因子負荷が0.4以上を太字にした。

	因子2 開放性	因子1 外向性	因子5 協調性	因子3 神経症傾向	因子4 勤勉性	共通性
A1	0.196	-0.138	-0.306	0.056	-0.080	0.115
A2	0.002	0.033	0.511	0.041	0.061	0.272
A3	-0.041	-0.043	0.581	0.010	0.005	0.363
A4	-0.089	-0.081	0.351	0.143	-0.114	0.205
A5	-0.097	-0.138	0.524	0.004	0.000	0.360
C1	0.094	-0.007	0.021	0.482	0.097	0.255
C2	0.093	0.089	0.066	0.587	0.008	0.337
C3	0.001	0.067	0.062	0.479	-0.012	0.230
C4	0.131	0.030	0.098	0.512	-0.058	0.315
C5	0.162	0.151	0.047	0.456	0.108	0.309
E1	-0.065	0.491	-0.057	0.081	-0.093	0.262
E2	0.079	0.588	-0.031	0.023	-0.051	0.408
E3	0.099	-0.344	0.222	0.016	0.181	0.279
E4	0.020	-0.466	0.314	0.041	-0.087	0.412
E5	0.132	-0.343	0.136	0.176	0.160	0.280
N1	0.723	-0.096	-0.083	0.009	-0.037	0.508
N2	0.688	-0.027	-0.077	0.007	0.020	0.472
N3	0.618	0.111	0.069	0.004	-0.001	0.426
N4	0.390	0.373	0.096	0.097	0.056	0.375
N5	0.410	0.178	0.123	0.033	-0.128	0.249
O1	0.043	-0.095	0.086	0.064	0.353	0.179
O2	0.134	-0.019	0.163	0.078	-0.411	0.214
O3	0.046	-0.132	0.128	0.036	0.429	0.268
O4	0.077	0.220	0.132	0.041	0.201	0.093
O5	0.104	-0.028	0.035	0.019	-0.459	0.215

順序変数で分析した結果が以前のエントリにあるが、因子負荷が高く、２値に変換して因子分析をると、0.4を切る項目出てきている。

因子分析の因子を作成することには基本的には成功しているが、推定結果は順序変数に劣る。IPIP-NEOのデータでは必ずしも正確に推定が行えたとは言えないだろう。以前のエントリでWISCのデータを用いて連続変数と４値の順序変数、2値のカテゴリカル変数で結果をシミュレーションをしたときには、結果はさほど変わらなかったが、今回は同様の結果を得られなかった。2値のカテゴリカル変数の因子分析は必ずしも、正確に推定できるわけではない、ということに気を付けたほうがよさそうだ。

潜在クラス分析の結果

IPIP-NEOのデータは6件法で測られていて、1が全くあてはまらない(Very Inaccurate)、6が非常にあてはまる(Very Accurate)となっているので、2値にしたときには、2の値の所属確率を見ていくことになる。0.7以上の値に太字をつけている。

	class 1	class 2	class 3	class 4	class 5	質問
所属確率	0.2852	0.3343	0.1497	0.1012	0.1297	-
A1	0.2519	0.1427	0.3085	0.1883	0.3384	他人の気持ちに無関心
A2	0.9559	0.9499	0.7032	0.9247	0.7001	他人の幸福にする方法を知っている
A3	0.9315	0.9471	0.5999	0.8631	0.5546	他人をなぐさめる方法を知っている
A4	0.8544	0.9401	0.6795	0.8119	0.5161	子供が大すき
A5	0.8936	0.9660	0.5906	0.9088	0.4534	人をくつろがせられる
C1	0.9286	0.9196	0.7755	0.5063	0.6187	仕事はしっかりとやる
C2	0.9064	0.8984	0.7783	0.2403	0.5972	物事は完成するまで続ける
C3	0.8496	0.9020	0.7529	0.3997	0.6019	計画通りに行動する
C4	0.2437	0.0636	0.2157	0.7276	0.5158	物事を中途半端にする
C5	0.5258	0.2278	0.4787	0.8958	0.8133	時間を無駄にする
E1	0.3153	0.2305	0.7145	0.1693	0.7028	あまり喋らない
E2	0.4666	0.1616	0.7188	0.3264	0.8919	他人へアプローチするのは難しい
E4	0.8520	0.9574	0.4195	0.9012	0.3116	簡単に友達を作る
E5	0.9037	0.9222	0.5314	0.7650	0.4304	世話をする
N1	0.7327	0.0657	0.1143	0.3390	0.7352	怒りやすい
N2	0.8997	0.2199	0.2772	0.5140	0.9345	イライラしやすい
N3	0.8342	0.1602	0.1695	0.3963	0.8377	気分が頻繁に変動する
N4	0.6383	0.1489	0.3663	0.4357	0.8971	しばしば気分がブルーになる
N5	0.6181	0.1655	0.2513	0.3165	0.6686	パニックになりやすい
O1	0.9208	0.9526	0.7705	0.8734	0.7389	アイデアが多くある
O2	0.3641	0.2229	0.2609	0.3957	0.3985	難しい読み物を避ける
O3	0.8943	0.9232	0.6494	0.8100	0.5998	会話のレベルを高める
O4	0.9365	0.8641	0.8449	0.8275	0.9333	物事を振り返って考える
O5	0.2271	0.1652	0.2094	0.2399	0.3458	物事を深くしらべない

一見して因子分析とは異なる結果になっていることがわかる。

O項目の傾向はどのクラスでもだいたい同じである。
O2「難しい読み物を避ける」とO5「物事を深くしらべない」はどのクラスでも低い。そもそもこれらの項目にYesと言っている人が少ないようだ。アイデアはたくさんあり、会話を面白く高められて、物事を振り返って考えてみるが、難しいものは読まないし、調べ物もしないという傾向がわかる。少し難しい本でも読んで、物事をしっかり調べないと、よいアイデアは出ない気がするし、会話のレベルも高くならない。解釈をすると悪口になってくるので、このあたりでやめておこう。

クラス１

クラス１はだいたいすべての項目で高く出ている。 E項目はE1「あまり喋らない」、E2「他人へアプローチするのは難しい」は低いが、E3「人を魅了する方法を知っている」E4「簡単に友達を作る」E5「世話をする」は高い。典型的なコミュニカティブな人である。N項目はすべて高く「神経症傾向」があることがわかる。

今までの経験では、潜在クラス分析はだいたいの項目があてはまるクラスが１つ作られるパターン、何もあてはまらないクラスが１つ作られるパターンが多かったように思う。個人的に経験した後者のパターンは逸脱・逆境環境系の質問を入れたときである。

簡単にまとめると、誰でも当てはまりそうな項目が多いときはだいたいの項目を満たすクラスが作られ、割と該当者が少ない項目が多いときはすべての項目に宛てはならないクスが作られる傾向があるということだ。もちろん、両方同時に起きることもある。今回は、前者のみ生じている。

クラス２

E項目はクラス１と同じ傾向でコミュニカティブなタイプである。N項目は割合が少なく「神経症傾向」がない。人としては社会に最も適応していそうな人だ。

クラス３

A3「他人をなぐさめる方法を知っている」、A4「子供が大すき」、A5「人をくつろがせられる」がやや低い。E1「あまり喋らない」、E2「他人へアプローチするのは難しい」の割合が高く、E3「人を魅了する方法を知っている」、E4「簡単に友達を作る」、E5「世話をする」の割合が少ない。
まとめると、人付き合いが苦手のようである。これはクラス５と同じ傾向だ。
ただ、N項目の「神経症傾向」の割合が低く、精神的な健康度は高そうである。

クラス４

最も近いのはクラス２である。しかし、C1「仕事はしっかりとやる」、C2「物事は完成するまで続ける」、C3「計画通りに行動する」の割合が低い。仕事や物事をしっかりとしないタイプである。

クラス５

クラス３と同じく人付き合いが苦手である。違いは、N項目の「神経症傾向」の割合が高いという点である。

結論と考察

IPIP-NEOのデータを用いて２値のカテゴリカル因子分析と潜在クラス分析をした結果、両者の結果は大きく異なることが判明した。
変数(概念)を基にしたグループ分けをする因子分析を、ケース(人)を基にしたグループ分けをする潜在クラス分析の特性がかなりよくわかるシミュレーションだったのではないかったかと思う。

心理学のリッカート尺度で計測するデータでは、今回のシミュレーションとよく似た結果、つまり全く結果が異なることが起こるのではないかと思う。因子分析ても潜在クラス分析でもどちらでもよい、とは言いづらいだろう。

データの特性などが変化すると、似たような結果がになる可能性も無くはないだろう。今回はN項目の「神経症傾向」が潜在クラス分析でもわりときれいに区別できていた。疾患を持っている人と、疾患を持っていない人というのは、連続的なのではなく、カテゴリカルに分かれているからであって、不思議はない。

精神医学的なインプリケーションとしては、精神疾患を順序変数で計測する流れへの評価であろうか。推進者が信じるほど利得は統計学的にはない。診断を現在の２値データで行うことに概念的にも、計量的にも問題がないと考えているのは、僕がカテゴリカル変数を扱う社会学出身であるからだけはなく、精神医学で統計の勉強をする人は心理学統計寄りの手技を勉強する傾向にあるため、カテゴリカル変数の扱い方を知らないのだと思う。

心理学的なインプリケーションとしては、リッカート尺度を用いた尺度研究をする際には、因子分析をした方がよく、潜在クラス分析は代替手段にはならないということだろう。

もう少し踏み込んだことをいうと、因子分析のみを行うことに大きな問題があるように思われる。Big5やNEOと呼ばれる研究群は、パーソナリティが５つに分かれるというが、その根拠が全くないことにとりあえず留意すべきである。５つの因子である開放性、外向性、協調性、神経症傾向、勤勉性が研究者の興味関心によって採用されたのだが、その５つに分かれるように質問項目を工夫して洗練させたのであって、そもそも人間のパーソナリティが5つに分かれるわけではない。3つでも6つでも概念を作成して、因子分析を繰り返して、Big3やBig6を作ることも可能である。

IPIP-NEOの25項目バージョンだけで結論を出すのは早計かもしれないが、潜在クラス分析をすると、IPIP-NEOの項目は、神経症傾向以外はバラバラに分類される。そもそも、１～２割くらいの人たちしか「そう思う」と答えていない項目あれば、逆にほとんどの人が「そう思う」と答えている項目もある。

それぞれの因子ごとに潜在クラス分析をしても固まって同じ傾向が出るくらいに質問文を精査した方がよい。因子分析をしてきれいに結果が分かれ、潜在クラス分析をすると、因子単位では少なくとも固まっていて、かつ、各項目が異なったことに関して問うている質問紙がベストである。単発の研究にそのようなことを望むのはやり過ぎだが、NEOの研究規模であれば、そのくらいはやっていて当然のような気がする。

因子分析とカテゴリカル因子分析の結果はとのくらい異なるか

ノーマルな因子分析は連続変数を用いる。その拡張としてカテゴリカル変数でも因子分析は可能である。今回は、連続変数で推定した結果とカテゴリカル因子分析の推定はどのくらい異なるのかをシミュレーションしてみたい。

大前提としてカテゴリカル変数といっても、その背景に連続変数、正規分布が仮定できなければならない。男女や東京に住んでいる、名古屋に住んでいるといった値は因子分析では扱えない。比較的有名な研究でも、「○○という体験をした」というマルチアンサーを因子分析したり、精神医学の診断を因子分析したりするものもあるが、因子分析を使うのは誤りである。どうしてもグルーピングがしたければ潜在クラス分析を使うべきである。

サンプルデータ

児童向けウェクスラー式知能検査（Wechsler Intelligence Scale for Children; WISC)のサンプルデータを用いてシミュレーションをしてみよう。サンプルデータはこちらやこちらからダウンロードする。

変数名	説明
info	Information
comp	Comprehension
arith	Arithmetic
simil	Similarities
vocab	Vocabulary
digit	Digit Span
pictcomp	Picture Completion
parang	Paragraph Arrangement
block	Block Design
object	Object Assembly
coding	Coding

それぞれの項目は20点満点(0～20)である。 WISCは階層構造になっているとされているが、面倒くさい上に、実データは教科書通りの因子構造をしていないので、そのまま因子分析にかけることにする。

データの加工

Rのpsychパッケージを利用して因子分析行う。

library(foreign)
d1 <- read.spss("wiscsem.sav", to.data.frame=TRUE)
d2 <- d1[3:13] # 因子分析に使用するのは3～13列目

リコード

今回は機械的に分位点で数値を分けていく。 OneRパッケージの分位点で連続変数を分けるbin functionを使う。

library(OneR)
d3 <- bin(d2, nbins = 4, labels = c(1,2,3,4))
d4 <- bin(d2, nbins = 2, labels = c(1,2))

d3は4分位で分けたデータをいれる。4段階の変数となる。d4には2分位で分けたデータを入れるので、２値データとなる。

データ型の変更

OneRでラベルをつけていることをみてもわかるように、データの中身はfactor型である。psychパッケージは整数型、つまりinteger型でないと作動しないので変換が必要になる。

いくつか方法があるようだが、dplyrパッケージを使う。コマンドはis.factorつまりfactor型である変数をas.integerintger型へ変換するという意味である。

library(dplyr)
d3 <- d3 %>% mutate_if(is.factor, as.integer)
str(d3) # データ構造の確認
d4 <- d4 %>% mutate_if(is.factor, as.integer)
str(d4) # データ構造の確認

因子数の決定

一応、手続きに則り、因子数の決定を行う。連続変数の方で行う。

スクリー・プロット

library("psych")
scree(d2,factors=TRUE,pc=TRUE,main="Scree plot",hline=NULL,add=FALSE)
VSS.scree(d2, main = "scree plot")  

平行分析

fa.parallel(d2)

MAP情報量

res01<-vss(d2) 
print(res01,digits =4)

スクリーは１因子、平行分析は２因子、Map情報量は2因子という提案であったため、2因子を採用する。

因子分析

連続変数での実施。

library("psych")
library("GPArotation")
res2 <- fa(d2, nfactors = 2, fm = "minres", rotate = "oblimin", scores=TRUE)
print(res2, digits = 3, sort=TRUE)

オプションで推定法(minres: 最小残差法)と回転(oblimin: オブリミン)をしているが、これはデフォルト値なので指定しなくてもよいが、結果を比較するので一応記述した。

４段階の順序変数での実施。corオプションは"poly"にする。

res02 <- fa(d3, nfactors = 2, fm = "minres", rotate = "oblimin",
                   scores=TRUE, cor="poly")
print(res02, digits = 3)

２値データでの因子分析。corオプションは"tet"にする。

res03 <- fa(d4, nfactors = 2, fm = "minres", rotate = "oblimin", 
                   scores=TRUE, cor="tet")
print(res03, digits = 3)

結果

因子１

	連続	４分位	２分位
info	0.831	0.816	0.978
comp	0.502	0.393	0.351
arith	0.604	0.621	0.453
simil	0.562	0.460	0.647
vocab	0.743	0.620	0.785
digit	0.487	0.392	0.353
pictcomp	0.063	-0.030	0.080
parang	0.095	-0.027	-0.082
block	0.057	0.040	0.087
object	-0.088	-0.027	-0.101
coding	0.101	0.084	-0.141

因子２

	連続	４分位	２分位
info	-0.075	-0.101	-0.085
comp	0.315	0.391	0.438
arith	-0.031	-0.037	0.335
simil	0.225	0.326	0.214
vocab	0.029	0.160	0.033
digit	-0.128	0.033	-0.023
pictcomp	0.587	0.670	0.679
parang	0.382	0.397	0.444
block	0.616	0.533	0.537
object	0.656	0.552	0.731
coding	-0.021	0.052	0.231

共通性(communalities)

	連続	４分位	２分位
info	0.63671	0.5943	0.8828
comp	0.50340	0.4594	0.4652
arith	0.34791	0.3641	0.4663
simil	0.48808	0.4657	0.5992
vocab	0.57303	0.5077	0.6421
digit	0.19385	0.1673	0.1175
pictcomp	0.38448	0.4302	0.5204
parang	0.18932	0.1479	0.1684
block	0.41647	0.3073	0.3411
object	0.38311	0.2908	0.4729
coding	0.00856	0.0141	0.0413

一つ一つ見るとめんどくさいが、ざっくりとまとめると、それほど値は変わらない。時々、違うものも混じっている。また、2分位より４分位の方が連続変数に近いというわけでもないようだ。

結果は、連続変数から作成したカテゴリカル変数であれば、もともとの連続変数の結果からは大きく外れない、というものだ。
ただ「逆も真なり」ではない。

調査データでは、連続変数からカテゴリカル変数に変換してカテゴリカル因子分析をするということはしない。連続変数があれば連続変数で分析するのがよいからだ。

実際には、背後に連続変数が想定されると考えられるカテゴリカル変数で因子分析をすることなる。連続変数が想定される根拠は無い。「おそらく想定されるであろう」という当て推量である。その当て推量があっている場合もあれば、見当はずれの場合もある。これは、いくらシミュレーションをしてもわからないもので、どうしようもない。カテゴリカル因子分析を使用する注意点はそのあたりだろうか。

StataでLassoとリッジ回帰

Stata16でLassoが新しく使えるようになったそうだ。
https://www.lightstone.co.jp/stata/stata16_new.html#Lasso

僕はStataはあまり使わないので、新しいStataを入手していない。今手元にあるものはバージョン13で少し古く、標準機能でLassoはできない。ただ、バージョン13以上であれば、パッケージとして作成されているlassopackが使用ができ、Lassoも問題なく使用することができる。

Stata Lasso
https://statalasso.github.io/

推定するパラメータ

最小二乗法

応答変数Y、n個の観測値、m個の予測変数、線形結合X、誤差項σ²。

リッジ回帰

正則化のペナルティλ。

Lasso回帰

Elastic Net

α=0の時にリッジ回帰、α=1の時にLasso、0≦α≦1がErastic Netである。パラメータはαとλの２つであるが、リッジ回帰とLassoのαは固定されているので、Erastic Netのことを考えないならば、λについてだけ考えればよい。

最適なラムダ

λの最適値を決める方法はいくつかある。

1. 相互検証 Cross-validation
2. 情報量基準(AIC, BIC, EBIC, AICc)
3. 理論に基づいたLasso

このエントリでは1と2を扱う。

lassopackパッケージのインストール

インストールは公式ページに書いてあるようにすればよい。 https://statalasso.github.io/installation/

ssc install lassopack
ssc install pdslasso

サンプルデータ

公式ページでは前立腺がんのデータが使われているので、ここでも同じデータを使おう。データの読み込みは下記のコマンドでできる。

insheet using ///
    https://web.stanford.edu/~hastie/ElemStatLearn/datasets/prostate.data,  ///
    clear tab

このデータは下記の項目が含まれている。

lpsa：PSAスコアの対数
lcavol：がんの体積
lweight：前立腺の重さの対数
年齢：患者の年齢
lbph：良性前立腺過形成の量のログ
svi：精嚢浸潤
lcp：被膜貫通の対数
gleason：グリーソン・スコア
pgg45：グリーソン・スコアが4または5のパーセンテージ

PSAスコアを対数変換したlpsaを従属変数にした重回帰分析でデモを行う。独立変数はlpsa以外全部である。この中から最も良い予測子を選ぶ。

情報量基準

まず情報量基準を用いて最適なλの値を推定をする。デフォルトではEBIC(Extended Bayesian Information Criterion)が使用されるようなので、EBICを使用する。

lasso2 lpsa lcavol lweight age lbph svi lcp gleason pgg45, lic(ebic)

lasso2がLassoのコマンド。lpsaが従属変数で、その後に続くのが独立変数である。これは、通常の回帰分析の書き方と同じである。最後にオプションとしてlic(aic)をつけると情報量基準が出せる。

  Knot|  ID     Lambda    s      L1-Norm        EBIC     R-sq   | Entered/removed
------+---------------------------------------------------------+----------------
     1|   1  163.62492     1     0.00000     31.41226   0.0000  | Added _cons.
     2|   2  149.08894     2     0.06390     26.66962   0.0916  | Added lcavol.
     3|   9   77.73509     3     0.40800    -12.63533   0.4221  | Added svi.
     4|  11   64.53704     4     0.60174    -18.31145   0.4801  | Added lweight.
     5|  21   25.45474     5     1.35340    -42.20238   0.6123  | Added pgg45.
     6|  22   23.19341     6     1.39138    -38.93672   0.6175  | Added lbph.
     7|  29   12.09306     7     1.58269    -39.94418   0.6389  | Added age.
     8|  35    6.92010     8     1.71689    -38.84649   0.6516  | Added gleason.
     9|  41    3.95993     9     1.83346    -35.69248   0.6567  | Added lcp.
Use 'long' option for full output.
Use lambda=27.93654463358689 (selected by EBIC).

---------------------------------------------------
         Selected |           Lasso   Post-est OLS
------------------+--------------------------------
           lcavol |       0.4725389      0.5258519
          lweight |       0.3989102      0.6617699
              svi |       0.4400748      0.6656665
------------------+--------------------------------
   Partialled-out*|
------------------+--------------------------------
            _cons |       0.2975585     -0.7771568
---------------------------------------------------

EBICによってて導かれたλの値が27.9である。上の表の3列目がλなので、その中から27.9以上のものを選択する。27.9以上だとlcavolとsviとlweightなので、この3つが最適なモデルとなる。この3つの変数で構成されたのが下の表である。独立変数(予測子)は少なめのモデルである。

Post-est OLSは3つの独立変数で重回帰分析をした結果が示されている。つまり、下記の重回帰の結果と同じである。

reg lpsa lcavol lweight svi

情報量基準による差異

情報量基準は4つ選択できるので、それぞれのλも計算しておこう。

Use lambda=7.594796178345335 (selected by AIC).  
Use lambda=27.93654463358689 (selected by BIC).  
Use lambda=27.93654463358689 (selected by EBIC).  
Use lambda=7.594796178345335 (selected by AICC).  

AIC系とBIC系のλが比較的違う。もし、AICを使用した場合、7.59以上なので、変数が比較的多くなる。下記のようなモデルになる。

Use lambda=7.594796178345335 (selected by AIC).

---------------------------------------------------
         Selected |           Lasso   Post-est OLS
------------------+--------------------------------
           lcavol |       0.5057140      0.5234981
          lweight |       0.5386738      0.6152349
              age |      -0.0073599     -0.0190343
             lbph |       0.0585468      0.0954908
              svi |       0.5854749      0.6358643
            pgg45 |       0.0022134      0.0035248
------------------+--------------------------------
   Partialled-out*|
------------------+--------------------------------
            _cons |       0.1243026      0.5214696
---------------------------------------------------

AICでλを決めると、8番目のgleasonと9番目のlcpが除かれた残りすべてが選択されている。AICを用いたLassoは一般的に変数の数が多くなる傾向にあるという指摘があるが、その傾向が表れているのかもしれない。

交差検証

交差検証(Cross-validation)は英語をそのまま読んだクロス・バリデーションと呼ばれることもある。データをトレーニングデータ（訓練事例集合 training set）と検証データ（テスト事例集合 testing set）に繰り返し分けて検証していく方法。つまり、データセットで解析をすると共に、その解析の妥当性をそのデータを用いて検証する方法である。トレーニングデータはモデルへのフィット、検証データは予測誤差の計算に使用する。

交差検証によってλの最適の値を特定し、αの予測パフォーマンスを最大化する。具体的に何をするかというと、平均二乗誤差推定値を最小になるλを求めることになる。

lassopackでは、K-分割交差検証 K-fold cross-validationを用いて交差検証をしている。

K-分割交差検証では、標本群をK個に分割する。そして、そのうちの1つをテスト事例とし、残る K − 1 個を訓練事例とするのが一般的である。交差検証は、K 個に分割された標本群それぞれをテスト事例として k 回検証を行う。そうやって得られた k 回の結果を平均して1つの推定を得る。
K-分割交差検証 - wikipedia

K-分割交差検証の実施

cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, seed(123)

cvlassoが交差検証のコマンド、オプションとして乱数のシードが指定できる。

K-fold cross-validation with 10 folds. Elastic net with alpha=1.
Fold 1 2 3 4 5 6 7 8 9 10
      |         Lambda           MSPE       st. dev.
----------+---------------------------------------------
         1|      163.62492      1.3238262      .22872507
         2|      149.08894      1.2300892      .22936459  
         3|      135.84429      1.1269313      .21564351  
...
        17|      36.930468      .59233725       .1113066  ^
...
        61|      .61603733       .5412582       .0566795  *
...
       100|      .01636249      .54145991      .05572026  
* lopt = the lambda that minimizes MSPE.
  Run model: cvlasso, lopt
^ lse = largest lambda for which MSPE is within one standard error 
            of the minimal MSPE.
  Run model: cvlasso, lse

実際の結果表示は100まで表示されるが、重要なのは^と*のあるところだけを表示している。MSPE(Mean Squared Prediction Error)とは、このセクションの冒頭で述べた最小平均二乗誤差推定値である。2列目はラムダの値である。MSPE(3列目)と標準誤差(4列目)から推定される。

平均二乗予測誤差を最小化するλ値は、アスタリスク*で示されている。^はその標準誤差内に入る最大のλの値である。

これらの交差検証の結果を用いてLassoを実行するには、下記のように書く。

cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, lopt seed(123)
cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, lse seed(123)

コマンドはcvlasso、オプションにloptもしくはlseを指定する。

. cvlasso, lopt
Estimate lasso with lambda=.616 (lopt).
---------------------------------------------------
         Selected |           Lasso   Post-est OLS
------------------+--------------------------------
           lcavol |       0.5567117      0.5643413
          lweight |       0.6152100      0.6220198
              age |      -0.0199971     -0.0212482
             lbph |       0.0935063      0.0967125
              svi |       0.7398081      0.7616733
              lcp |      -0.0907247     -0.1060509
          gleason |       0.0445775      0.0492279
            pgg45 |       0.0041720      0.0044575
------------------+--------------------------------
   Partialled-out*|
------------------+--------------------------------
            _cons |       0.1828371      0.1815609
---------------------------------------------------
. cvlasso, lse
Estimate lasso with lambda=36.93 (lse).

---------------------------------------------------
         Selected |           Lasso   Post-est OLS
------------------+--------------------------------
           lcavol |       0.4553753      0.5258519
          lweight |       0.3142849      0.6617699
              svi |       0.3674476      0.6656665
------------------+--------------------------------
   Partialled-out*|
------------------+--------------------------------
            _cons |       0.6435536     -0.7771568
---------------------------------------------------

K-分割交差検証のデメリットはいくつかある。

1. 最小平均二乗誤差推定値(MSPE)は乱数によって安定しない
2. MSPEは不安定性はサンプルサイズの小さい場合に顕著
3. 計算に時間がかかる(機械学習が目的ではない場合、この点は問題はない)

MSPEの不安定性を確認するには、乱数のシードを変えて(もしくは設定せずに)実施すると、どの程度か確認できるだろう。

適当にシードを指定して走らせてみた。

. cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, seed(234) lopt
Estimate lasso with lambda=.321 (lopt).
. cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, seed(298) lopt
Estimate lasso with lambda=1.562 (lopt).
. cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, seed(862) lopt
Estimate lasso with lambda=5.745 (lopt).

λの値は比較的異なる印象があるが、変数選択の個数に変化はみられなかった。変数選択という観点から見ると、このデモでは比較的安定しているように思えた。

プロット

Lassoでよく表示される、平均二乗予測誤差を縦軸に、λを横軸にしたプロットはplotcvオプションをつけると描画できる。

cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, seed(123) plotcv

リッジ回帰

lassopackでもリッジ回帰は計算できる。

lasso2 lpsa lcavol lweight age lbph svi lcp gleason pgg45, alpha(0)

オプションにalpha(0)をつけるだけで今まで説明してきた方法が同じように使える。デフォルト値がalpha(1)、つまりLassoなので、今まで特に何もオプションをつけなくてもLassoの計算がされていたということだ。

Rで相関プロットを描く

相関分析を視覚的に認識するために、相関プロットは有効である。特に、二次分析の際などに威力を発揮するかもしれない。二次分析は仮説があってそれを検証すために調査を作れるわけではないので、どの部分を分析するか、総当たりで検証することもあるからだ。やってみたらこうなった的で良くないプロセスだが、二次分析というビハインドがある場合には致し方ないこともあるだろう。

相関プロットを描画するにはcorrplotパッケージを利用する。

サンプルデータとしてMASSパッケージに含まれるBostonデータを使用する。比較的連続変数が多いデータである。

library(MASS)
data(Boston)
num <- c(1:3,5:8,10:14) # 連続変数は1~３、5~8、10~14列目。列番号をnumに格納。
d1 <- Boston[num] #連続変数だけのデータをd1に格納。

以下で相関プロットを作っていく。

library("corrplot")
res <- cor(d1, method = "pearson")
corrplot(corr = res, type="upper")

相関の強さが色の濃さと円の大きさで確認できる。

相関係数を重ねて描画することもできる。 オプションでaddCoef.colを付け加える。値は文字の色である。blackの方がわかりやすいかもしれない。

corrplot(corr = res, type="upper", addCoef.col="gray" )

これだと文字が重なってよくわからない。そういう場合には、画像サイズを先に指定しておくと解決できる。

png(height=800, width=800, pointsize=15, file="corrplot02.png")
corrplot(corr = res, type="upper", addCoef.col="black" )

heightは画像の高さ、widthは幅、pointsizeは文字の大きさで、file=はファイル名である。ファイルは作業ディレクトリに出力される。文字の重なりは、画像の大きさと文字の大きさを変更すると調整できる。

相関の強弱であればプラスかマイナスかはあまりどうでもいいという考え方もあるので、その場合には絶対値をつけてタイルで表示させるとオシャレ感が増す。

corrplot(corr = abs(res), method="color", tl.pos="n", cl.lim = c(0,1))

モザイクタイルのようなものが出来上がる。男子トイレに貼られることの多いタイル建材だ。

色を変えたいときには、以下のようにする。

corrplot(corr = abs(res), method="color", tl.pos="n",
          cl.lim = c(0,1), col=colorRampPalette(c("black","white","black"))(200))

白と黒だと印刷するときに便利かもしれない。 200と最後についているのは白から黒までの段階を何段階にするか、という指定である。

corrplot(corr = abs(res), method="color", addCoef.col="black",
              tl.pos="n", cl.lim = c(0,1))

相関係数の値も付与できる。

Rで共変量プロットを描く

Rで共変量プロットを描く。

library(AER)
data(CPS1985)
fit <- lm(formula = wage ~ education + age +
  　　　　 gender + occupation + union,
  　　　　 data = CPS1985)
summary(fit)

結果の表示。

Coefficients:
                     Estimate Std. Error t value Pr(>|t|)    
(Intercept)          -1.86545    1.37469  -1.357 0.175368    
education             0.59565    0.09350   6.370 4.13e-10 ***
age                   0.09476    0.01656   5.723 1.77e-08 ***
genderfemale         -1.81460    0.41555  -4.367 1.52e-05 ***
occupationtechnical   1.53776    0.68990   2.229 0.026240 *  
occupationservices   -1.34311    0.60762  -2.210 0.027507 *  
occupationoffice     -0.58774    0.63256  -0.929 0.353245    
occupationsales      -1.20902    0.81515  -1.483 0.138626    
occupationmanagement  2.82736    0.75765   3.732 0.000211 ***
unionyes              1.58683    0.50749   3.127 0.001865 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

信頼区間は次のように出力する。95%と90%を設定する。それぞれ5%有意と10%有意に相当する。

confint(fit, level = 0.95)
confint(fit, level = 0.90)

それぞれの結果の表示。

                        2.5 %     97.5 %
(Intercept)          -4.56604008  0.8351387
education             0.41196295  0.7793276
age                   0.06222812  0.1272862
genderfemale         -2.63095640 -0.9982519
occupationtechnical   0.18244561  2.8930780
occupationservices   -2.53677803 -0.1494321
occupationoffice     -1.83041166  0.6549327
occupationsales      -2.81038993  0.3923436
occupationmanagement  1.33895379  4.3157634
unionyes              0.58986138  2.5837930
                         5 %       95 %
(Intercept)          -4.13062657  0.3997252
education             0.44157788  0.7497127
age                   0.06747275  0.1220416
genderfemale         -2.49933668 -1.1298716
occupationtechnical   0.40096199  2.6745617
occupationservices   -2.34432325 -0.3418869
occupationoffice     -1.63005678  0.4545778
occupationsales      -2.55220306  0.1341567
occupationmanagement  1.57892791  4.0757893
unionyes              0.75060125  2.4230531

このままでは少し見づらいので、共変量プロットで図で確かめる。

library(coefplot)
coefplot(fit)

ゼロに掛かっていないものが有意である。横長のものが90%信頼区間で、短い方が95%信頼区間である。