Stata16でLassoが新しく使えるようになったそうだ。
https://www.lightstone.co.jp/stata/stata16_new.html#Lasso
僕はStataはあまり使わないので、新しいStataを入手していない。今手元にあるものはバージョン13で少し古く、標準機能でLassoはできない。ただ、バージョン13以上であれば、パッケージとして作成されているlassopackが使用ができ、Lassoも問題なく使用することができる。
Stata Lasso
https://statalasso.github.io/
推定するパラメータ
最小二乗法
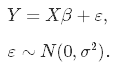
応答変数Y、n個の観測値、m個の予測変数、線形結合X、誤差項σ2。
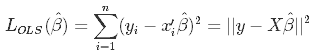
リッジ回帰
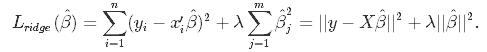
正則化のペナルティλ。
Lasso回帰
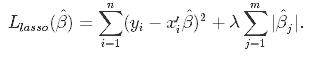
Elastic Net
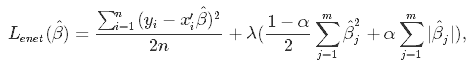
α=0の時にリッジ回帰、α=1の時にLasso、0≦α≦1がErastic Netである。パラメータはαとλの2つであるが、リッジ回帰とLassoのαは固定されているので、Erastic Netのことを考えないならば、λについてだけ考えればよい。
最適なラムダ
λの最適値を決める方法はいくつかある。
このエントリでは1と2を扱う。
lassopackパッケージのインストール
インストールは公式ページに書いてあるようにすればよい。 https://statalasso.github.io/installation/
ssc install lassopack ssc install pdslasso
サンプルデータ
公式ページでは前立腺がんのデータが使われているので、ここでも同じデータを使おう。データの読み込みは下記のコマンドでできる。
insheet using ///
https://web.stanford.edu/~hastie/ElemStatLearn/datasets/prostate.data, ///
clear tab
このデータは下記の項目が含まれている。
lpsa:PSAスコアの対数
lcavol:がんの体積
lweight:前立腺の重さの対数
年齢:患者の年齢
lbph:良性前立腺過形成の量のログ
svi:精嚢浸潤
lcp:被膜貫通の対数
gleason:グリーソン・スコア
pgg45:グリーソン・スコアが4または5のパーセンテージ
PSAスコアを対数変換したlpsaを従属変数にした重回帰分析でデモを行う。独立変数はlpsa以外全部である。この中から最も良い予測子を選ぶ。
情報量基準
まず情報量基準を用いて最適なλの値を推定をする。デフォルトではEBIC(Extended Bayesian Information Criterion)が使用されるようなので、EBICを使用する。
lasso2 lpsa lcavol lweight age lbph svi lcp gleason pgg45, lic(ebic)
lasso2がLassoのコマンド。lpsaが従属変数で、その後に続くのが独立変数である。これは、通常の回帰分析の書き方と同じである。最後にオプションとしてlic(aic)をつけると情報量基準が出せる。
Knot| ID Lambda s L1-Norm EBIC R-sq | Entered/removed
------+---------------------------------------------------------+----------------
1| 1 163.62492 1 0.00000 31.41226 0.0000 | Added _cons.
2| 2 149.08894 2 0.06390 26.66962 0.0916 | Added lcavol.
3| 9 77.73509 3 0.40800 -12.63533 0.4221 | Added svi.
4| 11 64.53704 4 0.60174 -18.31145 0.4801 | Added lweight.
5| 21 25.45474 5 1.35340 -42.20238 0.6123 | Added pgg45.
6| 22 23.19341 6 1.39138 -38.93672 0.6175 | Added lbph.
7| 29 12.09306 7 1.58269 -39.94418 0.6389 | Added age.
8| 35 6.92010 8 1.71689 -38.84649 0.6516 | Added gleason.
9| 41 3.95993 9 1.83346 -35.69248 0.6567 | Added lcp.
Use 'long' option for full output.
Use lambda=27.93654463358689 (selected by EBIC).
---------------------------------------------------
Selected | Lasso Post-est OLS
------------------+--------------------------------
lcavol | 0.4725389 0.5258519
lweight | 0.3989102 0.6617699
svi | 0.4400748 0.6656665
------------------+--------------------------------
Partialled-out*|
------------------+--------------------------------
_cons | 0.2975585 -0.7771568
---------------------------------------------------
EBICによってて導かれたλの値が27.9である。上の表の3列目がλなので、その中から27.9以上のものを選択する。27.9以上だとlcavolとsviとlweightなので、この3つが最適なモデルとなる。この3つの変数で構成されたのが下の表である。独立変数(予測子)は少なめのモデルである。
Post-est OLSは3つの独立変数で重回帰分析をした結果が示されている。つまり、下記の重回帰の結果と同じである。
reg lpsa lcavol lweight svi
情報量基準による差異
情報量基準は4つ選択できるので、それぞれのλも計算しておこう。
Use lambda=7.594796178345335 (selected by AIC). Use lambda=27.93654463358689 (selected by BIC). Use lambda=27.93654463358689 (selected by EBIC). Use lambda=7.594796178345335 (selected by AICC).
AIC系とBIC系のλが比較的違う。もし、AICを使用した場合、7.59以上なので、変数が比較的多くなる。下記のようなモデルになる。
Use lambda=7.594796178345335 (selected by AIC).
---------------------------------------------------
Selected | Lasso Post-est OLS
------------------+--------------------------------
lcavol | 0.5057140 0.5234981
lweight | 0.5386738 0.6152349
age | -0.0073599 -0.0190343
lbph | 0.0585468 0.0954908
svi | 0.5854749 0.6358643
pgg45 | 0.0022134 0.0035248
------------------+--------------------------------
Partialled-out*|
------------------+--------------------------------
_cons | 0.1243026 0.5214696
---------------------------------------------------
AICでλを決めると、8番目のgleasonと9番目のlcpが除かれた残りすべてが選択されている。AICを用いたLassoは一般的に変数の数が多くなる傾向にあるという指摘があるが、その傾向が表れているのかもしれない。
交差検証
交差検証(Cross-validation)は英語をそのまま読んだクロス・バリデーションと呼ばれることもある。データをトレーニングデータ(訓練事例集合 training set)と検証データ(テスト事例集合 testing set)に繰り返し分けて検証していく方法。つまり、データセットで解析をすると共に、その解析の妥当性をそのデータを用いて検証する方法である。トレーニングデータはモデルへのフィット、検証データは予測誤差の計算に使用する。
交差検証によってλの最適の値を特定し、αの予測パフォーマンスを最大化する。具体的に何をするかというと、平均二乗誤差推定値を最小になるλを求めることになる。
lassopackでは、K-分割交差検証 K-fold cross-validationを用いて交差検証をしている。
K-分割交差検証では、標本群をK個に分割する。そして、そのうちの1つをテスト事例とし、残る K − 1 個を訓練事例とするのが一般的である。交差検証は、K 個に分割された標本群それぞれをテスト事例として k 回検証を行う。そうやって得られた k 回の結果を平均して1つの推定を得る。
K-分割交差検証 - wikipedia
K-分割交差検証の実施
cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, seed(123)
cvlassoが交差検証のコマンド、オプションとして乱数のシードが指定できる。
K-fold cross-validation with 10 folds. Elastic net with alpha=1.
Fold 1 2 3 4 5 6 7 8 9 10
| Lambda MSPE st. dev.
----------+---------------------------------------------
1| 163.62492 1.3238262 .22872507
2| 149.08894 1.2300892 .22936459
3| 135.84429 1.1269313 .21564351
...
17| 36.930468 .59233725 .1113066 ^
...
61| .61603733 .5412582 .0566795 *
...
100| .01636249 .54145991 .05572026
* lopt = the lambda that minimizes MSPE.
Run model: cvlasso, lopt
^ lse = largest lambda for which MSPE is within one standard error
of the minimal MSPE.
Run model: cvlasso, lse
実際の結果表示は100まで表示されるが、重要なのは^と*のあるところだけを表示している。MSPE(Mean Squared Prediction Error)とは、このセクションの冒頭で述べた最小平均二乗誤差推定値である。2列目はラムダの値である。MSPE(3列目)と標準誤差(4列目)から推定される。
平均二乗予測誤差を最小化するλ値は、アスタリスク*で示されている。^はその標準誤差内に入る最大のλの値である。
これらの交差検証の結果を用いてLassoを実行するには、下記のように書く。
cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, lopt seed(123) cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, lse seed(123)
コマンドはcvlasso、オプションにloptもしくはlseを指定する。
. cvlasso, lopt
Estimate lasso with lambda=.616 (lopt).
---------------------------------------------------
Selected | Lasso Post-est OLS
------------------+--------------------------------
lcavol | 0.5567117 0.5643413
lweight | 0.6152100 0.6220198
age | -0.0199971 -0.0212482
lbph | 0.0935063 0.0967125
svi | 0.7398081 0.7616733
lcp | -0.0907247 -0.1060509
gleason | 0.0445775 0.0492279
pgg45 | 0.0041720 0.0044575
------------------+--------------------------------
Partialled-out*|
------------------+--------------------------------
_cons | 0.1828371 0.1815609
---------------------------------------------------
. cvlasso, lse
Estimate lasso with lambda=36.93 (lse).
---------------------------------------------------
Selected | Lasso Post-est OLS
------------------+--------------------------------
lcavol | 0.4553753 0.5258519
lweight | 0.3142849 0.6617699
svi | 0.3674476 0.6656665
------------------+--------------------------------
Partialled-out*|
------------------+--------------------------------
_cons | 0.6435536 -0.7771568
---------------------------------------------------
K-分割交差検証のデメリットはいくつかある。
- 最小平均二乗誤差推定値(MSPE)は乱数によって安定しない
- MSPEは不安定性はサンプルサイズの小さい場合に顕著
- 計算に時間がかかる(機械学習が目的ではない場合、この点は問題はない)
MSPEの不安定性を確認するには、乱数のシードを変えて(もしくは設定せずに)実施すると、どの程度か確認できるだろう。
適当にシードを指定して走らせてみた。
. cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, seed(234) lopt Estimate lasso with lambda=.321 (lopt). . cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, seed(298) lopt Estimate lasso with lambda=1.562 (lopt). . cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, seed(862) lopt Estimate lasso with lambda=5.745 (lopt).
λの値は比較的異なる印象があるが、変数選択の個数に変化はみられなかった。変数選択という観点から見ると、このデモでは比較的安定しているように思えた。
プロット
Lassoでよく表示される、平均二乗予測誤差を縦軸に、λを横軸にしたプロットはplotcvオプションをつけると描画できる。
cvlasso lpsa lcavol lweight age lbph svi lcp gleason pgg45, seed(123) plotcv
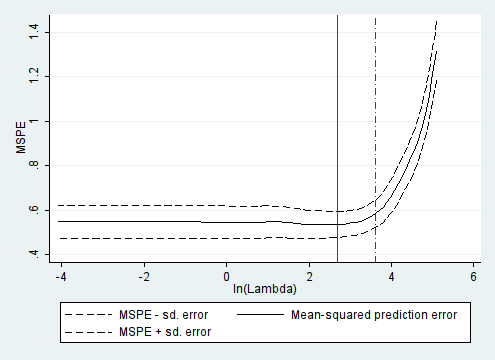
リッジ回帰
lassopackでもリッジ回帰は計算できる。
lasso2 lpsa lcavol lweight age lbph svi lcp gleason pgg45, alpha(0)
オプションにalpha(0)をつけるだけで今まで説明してきた方法が同じように使える。デフォルト値がalpha(1)、つまりLassoなので、今まで特に何もオプションをつけなくてもLassoの計算がされていたということだ。