ネット依存外来を設けている三光病院（同市牟礼町）の海野順院長が講師を務め、依存症が疑われる心身の状態などを紹介し、「依存症は誰もがなり得る。回復には周囲の支援が重要」と訴えた。
寺川知里さん（14）は「誰にでも依存症が起こり得ると初めて知った。休日についついネットを使い過ぎてしまうので気を付けたい」と話した。
こういうデマを流すのはやめてほしいものだ。
14歳の少女が精神病院で体験した｢極限の地獄｣(東洋経済)
考え続けた結果、Aさんが生育過程での母親との関係性の悪化について話をするときだけ、禅問答のような聞き返しがなく、Aさんの話を納得したように黙って聞いてくれることに気がついた。
「主治医はこの病気の原因を母親との親子関係に結び付ければ満足してくれるのだと思い、その方向で話を合わせるようになってからは、拘束が緩んでいくのが早くなりました」
そっち系か。
１４歳中学生を７７日間ベッドに拘束 摂食障害で入院の精神科に下った判決は(共同通信)
WLSMV を用いた測定の不変性の計算[Mplus]
Mplusで推定にWLSMV(adjusted diagonally weighted least squares)を使った測定の不変性の確認の方法について。
最尤法は正規分布と連続変数という2つの強力な仮定をすることから、順序尺度や正規分布にならないものの測定の不変性について確認する場合には、WLSMVや対角重みづけ最小二乗法などが向いている。
https://www.tandfonline.com/doi/abs/10.1080/10705511.2019.1602776
Wu and Estabrook (2016)の方法を解説している。
- Wu, H., & Estabrook, R. (2016). Identification of Confirmatory Factor Analysis Models of Different Levels of Invariance for Ordered Categorical Outcomes. Psychometrika, 81(4), 1014–1045. doi:10.1007/s11336-016-9506-0 https://link.springer.com/article/10.1007/s11336-016-9506-0
lavaanでの方法はこちらを参照のこと。内容は同じである。 ides.hatenablog.com
Mplusのコードはシンプルなものもあれば、非合理的な書き方を強いるものもあり、計算能力は優れているが、コードルールが優れているとはとても言えない。今回のコードはかなりややこしいので、もし可能であるならば、lavaanで行うことをお勧めしたい。
Wu & Estabrook(2016)の方法はよくある測定の不変性の計算と異なった考え方が異なる。
2016年に発表されたWu & Estabrookの論文では、グループ間の不変性検定の文脈で、順序付けられたカテゴリー結果のCFAにおける識別の問題を議論している。彼らのアプローチは、ME/Iを実施する現在のプラクティスとは異なる。現在のプラクティスでは、まずベースラインモデルを確立し、その後、パラメータ制限を増加させていく。Wu & Estabrookによると、現在のアプローチは最適ではないという。なぜなら、潜在的な連続反応の尺度に関してベースラインモデルがどのように特定されるかに依存しているためである。著者らは特に、閾値の古いモデルがどのように特定されるかに関心を持っている。様々な評価でリッカート型の項目が人気を博していることを考えると、データをカテゴリー的に扱うことは、検討やモデル化においてより重要になるだろう。したがって、我々の目標は、ME/Iのモデルの識別とテストに関してWu & Estabrookが提案した解決策に焦点を当てる。
サンプルのデータセットやコマンドはこちらに掲載されている。 figshare.com
データは2011年TIMSS 4thのbullyingスケールから4項目を利用(Mullis et al., 2009)。恣意的に選ばれた3つの国（31＝アゼルバイジャン、40＝オーストリア、246＝フィンランド）のデータを使用。すべての項目は0（まったくない）から3（少なくとも週に一度はある）までの4段階のリッカート尺度で測定されている。この尺度の項目では1年の間に学校で以下のようなことがどのくらいの頻度で起こったかを尋ねている。サンプルサイズはアゼルバイジャン、オーストリア、フィンランドでそれぞれ3808、4457、4520だった。
コード
ベースモデル
TITLE: Configural invariance for four items on bullying scale
DATA:
FILE IS 'BULLY.dat';
VARIABLE:
NAMES ARE IDCNTRY R09A R09B R09C R09D;
USEVARIABLES ARE IDCNTRY R09A R09B R09C R09D;
CATEGORICAL ARE R09A R09B R09C R09D;
GROUPING IS IDCNTRY (31=AZE 40=AUT 246=FIN);
ANALYSIS:
ESTIMATOR = wlsmv;
H1ITERATIONS = 3000;
MODEL:
y1 BY R09A@1; ! 負荷は常に1に固定されていなければならない
y2 BY R09B@1;
y3 BY R09C@1;
y4 BY R09D@1;
F1 BY y1-y4*;
F1@1;
[F1@0];
{R09A@1 R09B@1 R09C@1 R09D@1};
[y1-y4@0];
y1-y4@0; ! これは一種のファントム変数なので、残差分散は0である
[R09A$1-R09A$3*] ;
[R09B$1-R09B$3*] ;
[R09C$1-R09C$3*] ;
[R09D$1-R09D$3*] ;
MODEL AUT:
F1 BY y1-y4*;
F1@1;
[F1@0];
{R09A@1 R09B@1 R09C@1 R09D@1};
[y1-y4@0];
y1-y4@0;
[R09A$1-R09A$3*] ;
[R09B$1-R09B$3*] ;
[R09C$1-R09C$3*] ;
[R09D$1-R09D$3*] ;
MODEL FIN:
F1 BY y1-y4*;
F1@1;
[F1@0];
{R09A@1 R09B@1 R09C@1 R09D@1};
[y1-y4@0];
y1-y4@0;
[R09A$1-R09A$3*] ;
[R09B$1-R09B$3*] ;
[R09C$1-R09C$3*] ;
[R09D$1-R09D$3*] ;
OUTPUT:
tech1 tech4;
SAVEDATA:
DIFFTEST = prop4.dif; ! カイ二乗差検定用データの保存
データファイル(BULLY.dat)の1行目には1人目の受験者のデータが入っており、ヘッダや変数名は含まれていない。USEVARIABLESのには、解析に使用する変数が記載される。これらの変数名はMODEL部分に表示されることになっている。グループ化変数IDCNTRYには、国の識別コードに関連する値が含まれている。この場合、グループ化変数には、31（Azerbaijan）、40（Australia）、24（Finland）の3つのグループが含まれている。
GROUPING IS IDCNTRY (31=AZE 40=AUT 246=FIN);
31アゼルバイジャン、40オーストリア、246フィンランドの3つのグループが含まれている。
観測された変数がカテゴリカルであることからWLSMV(ロバスト重み付き最小二乗法)を使用する。
ESTIMATOR = wlsmv; ! 順序変数の推定
h1iterations = 3000; !Mpusのデフォルトの値。欠損データを含む無制限モデルの最大反復回数。y1 BY R09A@1; y2 BY R09B@1; y3 BY R09C@1; y4 BY R09D@1;
MODELコマンドの最初の4行は、潜在変数y*を指定するためのファントム変数を示す。負荷は常に1に固定されている。
F1@1;
[F1@0];
すべてのグループの因子平均[F1@0]と分散F1@1はそれぞれ0と1に設定されている。
{R09A@1 R09B@1 R09C@1 R09D@1};
因子尺度{R09A@1 R09B@1 R09C@1 R09D@1}はすべてのグループで1に固定されている。
[y1-y4@0];
y1-y4@0;
切片の平均[y1-y4@0]と残差分散y1-y4@0も0に固定されている。
BY y1-y4 ! すべてのグループで推定される負荷量
[R09A$1-R09A$3] ; ! すべてのグループで推定されるしきい値
[R09B$1-R09B$3] ;
[R09C$1-R09C$3] ;
[R09D$1-R09D$3*] ;
このモデルはベースライン・モデルなので、閾値と負荷量はグループ間で自由に推定されることが予想されるため、アスタリスクを使用する。
SAVEDATA: DIFFTEST = prop4.dif;
分析の次のステップでANALYSISコマンドで読み込むカイ二乗差検定に必要な情報を生する。すなわち、Proposition 4 (Wu & Estabrook, 2016)のように等しい閾値を制約する場合には、file prop4.difを入力する。
Proposition 4
thresholds invarianceを求めるコードである。
TITLE: Proposition 4 (thresholds invariance) for four items on bullying scale
DATA:
FILE IS 'BULLY.dat';
VARIABLE:
NAMES ARE IDCNTRY R09A R09B R09C R09D;
USEVARIABLES ARE IDCNTRY R09A R09B R09C R09D;
CATEGORICAL ARE R09A R09B R09C R09D;
GROUPING IS IDCNTRY (31=AZE 40=AUT 246=FIN);
ANALYSIS:
ESTIMATOR = wlsmv;
DIFFTEST = prop4.dif;
H1ITERATIONS = 3000;
MODEL:
y1 BY R09A@1; ! Loadings must always be fixed to 1 here
y2 BY R09B@1;
y3 BY R09C@1;
y4 BY R09D@1;
F1 BY y1-y4*;
F1@1; !fixed to 1 in all groups
[F1@0]; !factor means fixed to 0 in all groups
{R09A@1 R09B@1 R09C@1 R09D@1};!factor scale fixed to 1 in G1, estimated in others
[y1-y4@0]; ! intercepts means fixed to 0 in group 1, others estimated
y1-y4@0; ! Because this is a kind of phantom variable, residual variance is 0
[R09A$1-R09A$3*] (T1-T3); !constrain thresholds to be equal across groups
[R09B$1-R09B$3*] (T4-T6);
[R09C$1-R09C$3*] (T7-T9);
[R09D$1-R09D$3*] (T10-T12);
MODEL AUT:
F1 BY y1-y4*;
F1@1; !fixed to 1 in all groups
[F1@0]; !factor means fixed to 0 in all groups
{R09A* R09B* R09C* R09D*};!factor scale fixed to 1 in G1, estimated in others
[y1-y4*]; !estimated in all but G1
y1-y4@0;
[R09A$1-R09A$3*] (T1-T3);
[R09B$1-R09B$3*] (T4-T6);
[R09C$1-R09C$3*] (T7-T9);
[R09D$1-R09D$3*] (T10-T12);
MODEL FIN:
F1 BY y1-y4*;
F1@1; !fixed to 1 in all groups
[F1@0]; !factor means fixed to 0 in all groups
{R09A* R09B* R09C* R09D*}; !factor scale fixed to 1 in G1, estimated in others
[y1-y4*]; !estimated in all but G1
y1-y4@0;
[R09A$1-R09A$3*] (T1-T3);
[R09B$1-R09B$3*] (T4-T6);
[R09C$1-R09C$3*] (T7-T9);
[R09D$1-R09D$3*] (T10-T12);
OUTPUT:
tech1 tech4;
SAVEDATA:
DIFFTEST = prop7.dif;
!This produces the necessary information for the chi-square difference test that
!we will read in in the "ANALYSIS" command in the next step for equal slopes and t-holds
DIFFTEST = prop4.dif;
前のベースモデルで検討されたファイルを使用する。
モデル・アイデンティフィケーションの制約として、切片の平均は、第1グループ[y1-y4@0]では0に固定され、残りのすべてのグループ[y1-y4]では推定され、Yの分散は1に固定され、すべてのグループで次のようになる。
因子平均κg=0[F1@0]と因子分散F1@1は1に固定（diag((Φg)=I). (T1-T3)...(T10-T12)を介して閾値に制約を加える。
SAVEDATA: DIFFTEST = prop7.dif;
前回と同じように今回のステップでのカイ二乗検定を保存しておく。
Proposition 7
TITLE: Proposition 7 (thresholds and loading invariance) for four items on bullying scale
DATA:
FILE IS 'BULLY.dat';
VARIABLE:
NAMES ARE IDCNTRY R09A R09B R09C R09D;
USEVARIABLES ARE IDCNTRY R09A R09B R09C R09D;
CATEGORICAL ARE R09A R09B R09C R09D;
GROUPING IS IDCNTRY (31=AZE 40=AUT 246=FIN);
ANALYSIS:
ESTIMATOR = wlsmv;
DIFFTEST = prop7.dif;
H1ITERATIONS = 3000;
MODEL:
y1 BY R09A@1; ! Loadings must always be fixed to 1 here
y2 BY R09B@1;
y3 BY R09C@1;
y4 BY R09D@1;
F1 BY y1-y4* (L1-L4); !constrain loadings across groups;
F1@1; !fixed to 1 in G1
[F1@0]; !factor means fixed to 0 in all groups
{R09A@1 R09B@1 R09C@1 R09D@1};!factor scale fixed to 1 in G1, estimated in others
[y1-y4@1]; !estimated intercepts means fixed to 1 in group 1, others estimated
y1-y4@0; ! Because this is a kind of phantom variable, residual variance is 0
[R09A$1-R09A$3*] (T1-T3); !constrain thresholds to be equal across groups
[R09B$1-R09B$3*] (T4-T6);
[R09C$1-R09C$3*] (T7-T9);
[R09D$1-R09D$3*] (T10-T12);
MODEL AUT:
F1 BY y1-y4* (L1-L4); !constrain loadings across groups;
F1*; !estimated in all but G1
[F1@0]; !factor means fixed to 0 in all groups
{R09A* R09B* R09C* R09D*};!factor scale fixed to 1 in G1, estimated in others
[y1-y4*]; !estimated in all but G1 where it is fixed to 1 (change to 0 if not working)
y1-y4@0;
[R09A$1-R09A$3*] (T1-T3);
[R09B$1-R09B$3*] (T4-T6);
[R09C$1-R09C$3*] (T7-T9);
[R09D$1-R09D$3*] (T10-T12);
MODEL FIN:
F1 BY y1-y4* (L1-L4); !constrain loadings across groups;
F1*; !estimated in all but G1
[F1@0]; !factor means fixed to 0 in all groups
{R09A* R09B* R09C* R09D*}; !factor scale fixed to 1 in G1, estimated in others
[y1-y4*]; !estimated in all but G1
y1-y4@0;
[R09A$1-R09A$3*] (T1-T3);
[R09B$1-R09B$3*] (T4-T6);
[R09C$1-R09C$3*] (T7-T9);
[R09D$1-R09D$3*] (T10-T12);
OUTPUT:
tech1 tech4;
今回のステップでも前回のステップでのカイ二乗検定の情報を利用する。
DIFFTEST = prop7.dif;
部分開放
部分不変の例は、閾値と負荷不変のモデルの修正に基づいて取られ、修正指標によって導かれる。最も厳しいモデルから始めて、等しい閾値のモデルを保持していたので、負荷のみに焦点を当てて修正指標を要求していく。部分的な測定不変性の探索を呼び出すためのMplusのシンタックスは、OUTPUTコマンドのmodindices(3.84)である。
OUTPUT: tech1 tech4 modindices(3.84);
MODEL MODIFICATION INDICES
NOTE: Modification indices for direct effects of observed dependent variables
regressed on covariates and residual covariances among observed dependent
variables may not be included. To include these, request MODINDICES (ALL).
Minimum M.I. value for printing the modification index 3.840
M.I. E.P.C. Std E.P.C. StdYX E.P.C.
Group AZE
BY Statements
Y1 BY R09A 15.285 0.252 0.183 0.183
Y1 BY R09C 90.471 -0.629 -0.457 -0.457
Y1 BY R09D 17.423 0.262 0.190 0.190
Y2 BY R09A 15.285 0.259 0.183 0.183
Y2 BY R09C 90.471 -0.648 -0.457 -0.457
Y2 BY R09D 17.423 0.270 0.190 0.190
Y3 BY R09A 15.285 0.240 0.183 0.183
Y3 BY R09C 90.471 -0.598 -0.457 -0.457
Y3 BY R09D 17.423 0.249 0.190 0.190
Y4 BY R09A 15.285 0.250 0.183 0.183
Y4 BY R09C 90.471 -0.626 -0.457 -0.457
Y4 BY R09D 17.423 0.260 0.190 0.190
F1 BY R09A 15.285 0.183 0.183 0.183
F1 BY R09C 90.471 -0.457 -0.457 -0.457
F1 BY R09D 17.423 0.190 0.190 0.190
ここで着目するのはMI値である。MI値が最も高い部分の負荷を解放すると部分不変性が得られることが多い。
R09Cのロードを解放することで、fitが最も改善されることがわかる。 Mplusでのこれらの値は、MIAZE = 90.471、MIAUT < 3.84、MIFIN = 40.327である。
モデルの修正
F1 BY R09Cを解放するため、次のように書く。MODEL AUTの部分である。
MODEL AUT: F1 BY y1-y4* (L1-L4); !constrain loadings across groups;
F1 BY y3のみ(L3)の制約を外す。
MODEL AUT: F1 BY y1 (L1); !constrain loadings across groups; F1 BY y2 (L2); F1 BY y3; !freely estimate F1 BY y4 (L4);
MODEL FIN:も同様の表記にする。
ME/Iアプローチの最新動向に関する簡単なメモ
部分的不変性アプローチに加えて、研究者たちはME/Iの達成に失敗することに対処するいくつかの方法を提案している。以下では、ME/Iを体系的に検討しようとしたいくつかの研究(Asparouhov & Muthen, 2014; Finch & French, 2018; Pokropek, Davidov, & Schmidt, 2019; Raykov et al.,2012)のうち、ME/Iの分野で期待される手法やアプローチを利用/提案しているものを、簡潔に紹介する。 MG-CFAの比較的新しいアプローチであるアライメント法（Asparouhov & Muthen, 2014）は、測定の妥当性を確立する従来の方法に代わるである。アライメント法は、典型的なMG-CFAとは異なり、測定の不変性を前提としていない。むしろ、この方法は、グループ間のパラメーター不変性を最小化する最適なソリューションを特定する。アライメント法の特徴は、すべてのモデル・パラメータ（因子平均、因子分散、負荷量、切片/閾値、および残差分散）を推定する際に、ソリューションが既存のソリューションまたはベースライン・ソリューションと同一のフィット示すことである。これは、潜在変数の平均と分散がそれぞれ0と1の値に固定されていると仮定しているコンフィギュラルコン不変モデルとは対照的であろう。このような潜在変数の標準化は，潜在変数が同じ尺度ではないことを意味し，その結果，比較することができない。アライメント法は、比較群の数が多い場合のパラメータの等質性の検定に関連する問題を克服する実用的な方法であるが、この方法は本質的には探索的なものであり、Pokropek et al.（2019）の研究で示唆されたように、その性能は条件によって異なる。 Raykovら（2012）は、Benjamini-Hochberg（BH）偽発見率法を使用し、ファミリー全体の誤り率を事前に設定したシグニフィカンスレベルに制御する、ME/Iの検査に適した多重検定手順を概説した10。著者らが述べているように、BHアプローチは、ME/Iの全体的な評価を可能にするだけでなく、異なる、より局所的な不変性のレベルをテストすることを可能にするという点で柔軟性がある（すなわち、負荷または切片の不変性のみをテストする）。 最近、Pokropekら（2019）は、ME/Iをテストするための伝統的なアプローチと新しいアプローチを調査した。大規模なシミュレーション研究において、著者らは、MG-CFA、部分的MG-CFA、マルチグループ・ベイズ構造方程式モデリング（SEM）、部分的マルチグループ・ベイズSEM、アライメント最適化を伴うMG-CFAなど、ME/Iのテストに使用される5つの手法のパフォーマンスを調べた。Pokropekらの全体的な結論は、次のように要約できる。部分的測定不変性は、多くの項目が不変である場合に、パス係数と潜在的平均を復元するのに適した（効果的な）方法かもしれない。近似測定不変性モデルは、多くのパラメータがほぼ（正確ではないが）等しい場合に、潜在的平均を復元するのに使用するのがより適切かもしれない。一方、アライメント法は、少数の不変パラメータが存在する場合に、潜在的平均を復元するのに適切かもしれない。著者らが示唆しているように、これらの手法のいくつか（特に、より柔軟性のあるもの）について、より良い収束とより効率的なアルゴリズムの観点から、今後の研究が望まれるす。 最後に、FinchとFrench（2018）は、YuanとChan（2016）、MarcoulidesとYuan（2017）、Yuan、Chan、Marcoulides、Bentler（2016）が説明したRMSEAの同等性検定アプローチの有用性を検討しましたが、YuanとChanの研究では、単一のデータセットで有望視されていました。提案された同等性検定のアプローチは、タイプI（およびII）エラー（複数可）をコントロールする上でのカイ二乗差検定の不十分さへの対応としても生まれました。そこで、FinchとFrenchは、メトリック不変性とスカラー不変性の両方を検証するシミュレーション研究を通じて、その性能を系統的に検証しました（すなわち、不変性はそれぞれ荷重と切片に存在するとモデル化されました）。著者らは、指標が正規分布していると仮定したモデルに等価アプローチを用いることを支持しており、さらに重要な点として、不変性が存在するかどうかの程度に関する有用な情報を提供する能力を指摘しています。これは、著者らが述べているように、ME/Iに対するより伝統的なアプローチとは対照的であり、一般的には不変性の有無という結論を導き出すものである。
- Asparouhov, T., & Muthén, B. O. (2014). Multiple-group factor analysis alignment. Structural Equation Modeling: A Multidisciplinary Journal, 21(4), 495–508. doi:10.1080/10705511.2014.919210
- Finch, H. W., French, B. F., & Finch, M. E. (2018). Comparison of methods for factor invariance testing of a 1-factor model with small samples and skewed latent traits. Frontiers in Psychology, 9, 332. doi:10.3389/fpsyg.2018.00332
- Pokropek, A., Davidov, E., & Schmidt, P. (2019). A Monte Carlo Simulation Study to Assess The Appropriateness of Traditional and Newer Approaches to Test for Measurement Invariance. Advanced online publication. Structural Equation Modeling: A Multidisciplinary Journal, 1–21. doi:10.1080/10705511.2018.1561293
- Raykov, T., Marcoulides, G. A., & Millsap, R. E. (2012). Factorial invar- iance in multiple populations: A multiple testing procedure. Educational and Psychological Measurement, 73, 713–727. doi:10.1177/0013164412451978
- Yuan, K.-H., & Chan, W. (2016). Measurement invariance via multigroup SEM: Issues and solutions with chi-square difference tests. Psychological Methods, 21(3), 405–426. doi:10.1037/met0000080
- Marcoulides, K. M., & Yuan, K.-H. (2017). New ways to evaluate good- ness of fit: A note on using equivalence testing to assess structural equation models. Structural Equation Modeling. A Multidisciplinary Journal, 24, 148–153.
- Yuan, K.-H., Chan, W., Marcoulides, G. A., & Bentler, P. M. (2016). Assessing structural equation models by equivalence testing with adjusted fit indexes. Structural Equation Modeling, 23(3), 319–330. doi:10.1080/10705511.2015.1065414
LatentGOLDで潜在クラス分析[LatentGOLD]
日本語では潜在クラス分析と呼ぶことが多いが、他の潜在クラスモデルと区別するために、潜在クラス・クラスター・モデル(Latent Class Cluster Model)とも言われる。
データ
RのpoLCAパッケージからvalueデータを使用する。
library("poLCA")
data("values",package="poLCA")
データ
A B C D 1 2 2 2 2 2 2 2 2 2 3 2 2 2 2 4 2 2 2 2 5 2 2 2 2 6 2 2 2 2
データの説明は下記のように書かれている。
「普遍的な価値観」または「特殊な価値観」の傾向を測定する4つの質問（A、B、C、D）に対する216人の回答者の二分法による調査結果。このデータセットは、Goodman (2002, p. このデータセットは、Goodman (2002, p. 14)に表4として掲載されており、以前はGoodman (1974)とStouffer and Toby (1951)に掲載されていた。
サンプルデータなので、特にデータの理解は不要だろう。
havenパッケージでSPSS形式で出力する。
library(haven) write_sav(values, "values.sav")
エリアの呼び方
LatentGOLDの左のエリアはアウトラインペイン、右はコンテンツペインと呼ぶらしい。
データを開く
データ名values.savをクリックすると下記のような画面になる。
分析の開始
Model1を右クリック[Cluster]もしくは、メニューの[Model]の[Cluster]をクリックする。
潜在クラス分析を行う変数を[Indicators]の中に入れる。
[Indicators]にいれた後、右クリックし、データタイプを[Nominal]にする。
[scan]を押すと、単純集計がみられるようになる。
AをダブルクリックするとAの変数の集計が見られる。
クラスター数の指定
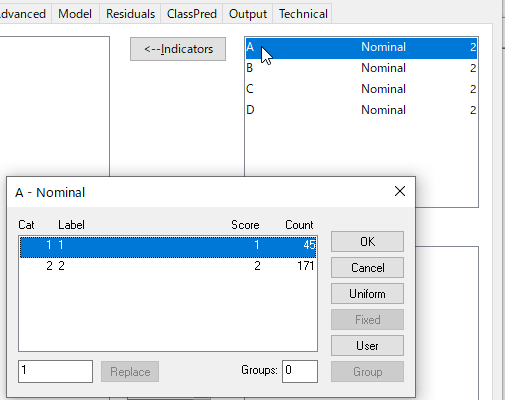
試行錯誤が必要なところだが、とりあえず1から5くらいに指定しておこう。
実行
[Estimete]をクリック。
全体の結果
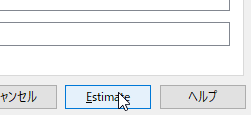
values.savのところをクリックすると全体の結果がみれる。「ｲ」となっているのは正しくは２乗表記がされるはずなのだが、バグっている。原因は、使っているWindowsの標準言語を日本語に設定しているためではないかと思っているが、よくわからない。
クラス数の決定の解釈1
クラスター数を決定する1つの基準は、L²統計量がカイ二乗分布に従うと仮定した場合の各モデルのp-値を示す「p-値」列を見ることである。一般的には、p値が0.05より大きい（十分な適合性がある）モデルの中で、最も解析的なモデル（パラメータの数が最も少ない（Npar））が選択される。この基準を用いると、最適なモデルはモデル2の2クラスタモデル（p値0.82、Npar=9）となる。
BLRT 条件付きブートストラップによるモデル改善の評価
今回は1クラスと2クラスを比較する。
2クラスなので、比較できるのは2と1クラスのみである。
4クラスの場合は3クラスと、一つ少ないクラスと比較するのが通常の使い方である。
結果。
有意であるということは、1クラスより2クラスの方がモデルが改善されているということであるため、BLRTは2クラスモデルを支持していない。5%以上になるまで繰り返そう。
パラメータの出力を見る
パラメータを見るには[+]で開いていく。
プロフィール
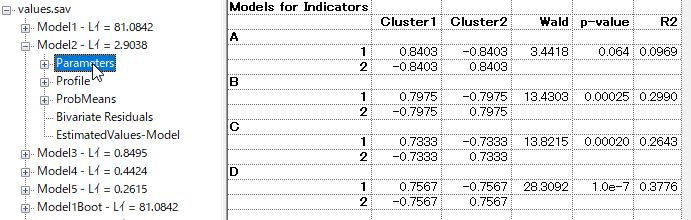
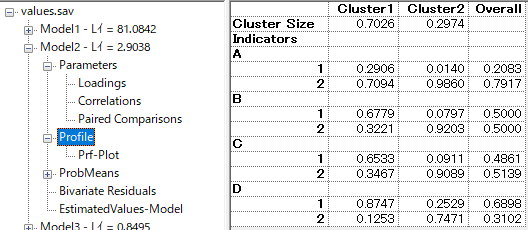
所属クラスと、A-Dの所属確率が表示される。
プロフィール・プロット
ユニ・プロット
トリ・プロット
定義ファイルの保存
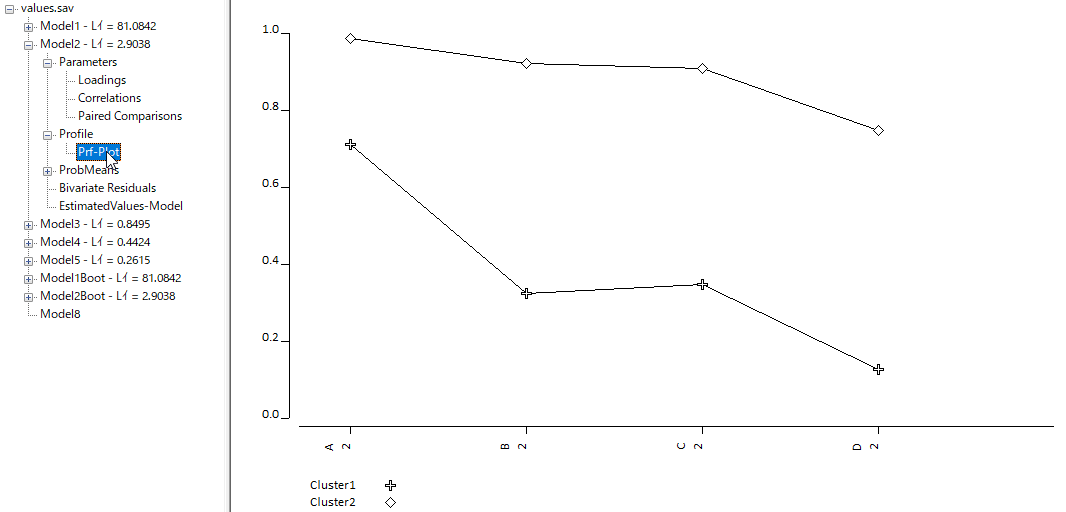
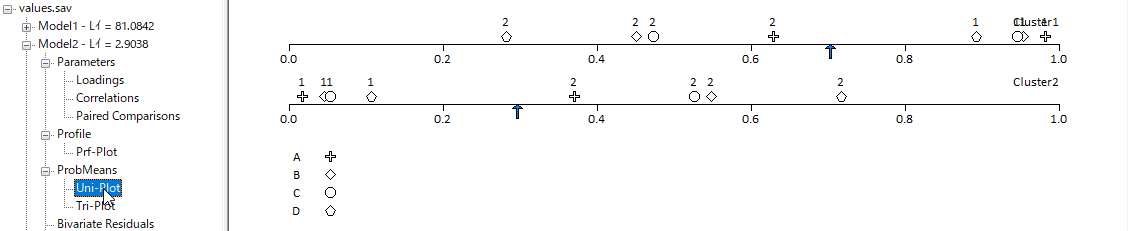
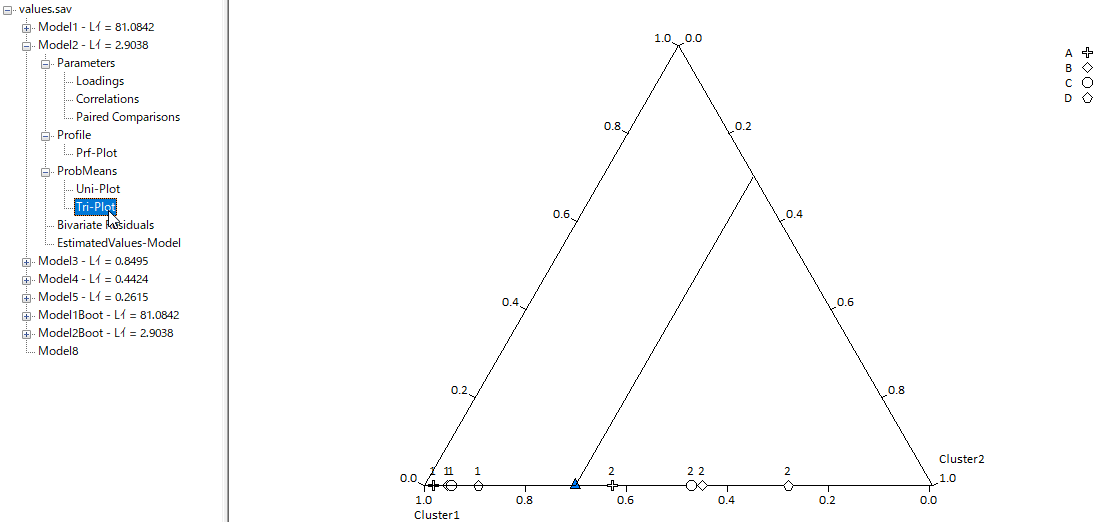
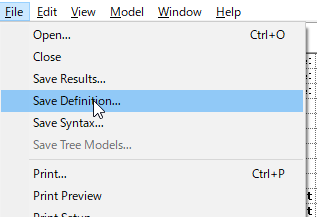
保存したいモデルを選択し、[File]から定義ファイルを.lgf形式で保存することができる。
INDIGOネットワークメンバーによるメンタルヘルス関連のスティグマや差別に関する出版物
日本でメンタルヘルス系で研究をしているのは医学系の人らしい。
ガンマ分布のglm()モデリング[R]
Kazuki Yoshidaさんによって作成されたものらしい。
farawayパッケージに含まれる半導体ウェハのデータを用いる。
library(faraway) data(wafer) plot(density(wafer$resist))
結果は連続的なものだが、右に傾いており、常に正の値を示している。このようなデータを分析する最も一般的な方法は、結果を対数変換することである。しかし、一般化線形モデルの枠組みの中で、より良い代替手段がある。
"resitivity of wafer in semiconductor experiment"
Description:
A full factorial experiment with four two-level predictors.
Format:
A data frame with 16 observations on the following 5 variables.
x1 a factor with levels ‘-’ ‘+’
x2 a factor with levels ‘-’ ‘+’
x3 a factor with levels ‘-’ ‘+’
x4 a factor with levels ‘-’ ‘+’
resist Resistivity of the wafer
Source:
Myers, R. and Montgomery D. (1997) A tutorial on generalized
linear models, Journal of Quality Technology, 29, 274-291.
用語解説 算術平均とは通常の平均である。 geometric mean（幾何平均）は、算術平均を対数スケールで計算したものである。
ここでは，オッズ比やレート比と同じように，2つの平均値を比較する比率を表すために「平均比」を使っている。
通常の方法 - 結果を対数変換した線形モデル（乗法幾何平均モデル）
res.lm.logY <- lm(log(resist) ~ x1 + x2 + x3 + x4, data = wafer) summary(res.lm.logY)
Call:
lm(formula = log(resist) ~ x1 + x2 + x3 + x4, data = wafer)
Residuals:
Min 1Q Median 3Q Max
-0.1757 -0.0622 0.0175 0.0877 0.1084
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.4405 0.0598 90.95 < 2e-16 ***
x1+ 0.1228 0.0535 2.29 0.04243 *
x2+ -0.2999 0.0535 -5.60 0.00016 ***
x3+ 0.1784 0.0535 3.34 0.00665 **
x4+ -0.0561 0.0535 -1.05 0.31652
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.107 on 11 degrees of freedom
Multiple R-squared: 0.816, Adjusted R-squared: 0.75
F-statistic: 12.2 on 4 and 11 DF, p-value: 0.000491
exp(coef(res.lm.logY))
(Intercept) x1+ x2+ x3+ x4+ 230.5536 1.1306 0.7409 1.1953 0.9454
結果が歪んでいて常に正である場合は、変換することでモデル化することができる。このモデルは次のようにモデル化している。
このように、対数スケールでの（算術的）平均変化、つまり、元のスケールでの幾何学的な「平均比」という観点からのみ解釈される。
例えば、x1＝＋とすると、対数結果の期待値（算術平均）は0.12277変化する。両辺の指数をとった共変量 は、元の結果の幾何平均を掛け合わせた比率（元の尺度での幾何平均比）である。
切片を指数化したもの は、すべての予測因子について-を持つウェハの幾何平均の期待値である。
したがって，このモデルは，予測変数による元の結果への乗法的効果を仮定している。
代替案1 - ガンマファミリとログリンクを用いた一般化線形モデル（乗算算術平均モデル）
res.glm.Gamma.log <- glm(formula = resist ~ x1 + x2 + x3 + x4,
family = Gamma(link = "log"),
data = wafer)
summary(res.glm.Gamma.log)
Call:
glm(formula = resist ~ x1 + x2 + x3 + x4, family = Gamma(link = "log"),
data = wafer)
Deviance Residuals:
Min 1Q Median 3Q Max
-0.17548 -0.06486 0.01423 0.08399 0.10898
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.44552 0.05856 92.983 < 2e-16 ***
x1+ 0.12115 0.05238 2.313 0.041090 *
x2+ -0.30049 0.05238 -5.736 0.000131 ***
x3+ 0.17979 0.05238 3.432 0.005601 **
x4+ -0.05757 0.05238 -1.099 0.295248
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for Gamma family taken to be 0.01097542)
Null deviance: 0.69784 on 15 degrees of freedom
Residual deviance: 0.12418 on 11 degrees of freedom
AIC: 152.91
Number of Fisher Scoring iterations: 4
exp(coef(res.glm.Gamma.log))
(Intercept) x1+ x2+ x3+ x4+ 231.7186 1.1288 0.7405 1.1970 0.9441
結果が歪んでいて常に正である場合は、ガンマ分布を用いてモデル化することができる。
リンク関数は、先の線形モデルとの整合性を考慮してlog()とし、以下のようにモデル化している。
となり、以下も成立する。
このように、元の尺度での算術平均を推論することができる。
例えば、x1 = +とすると、対数算術平均結果が0.12115増加する。両辺の指数を取った共変量 は、元の尺度での算術平均の結果に乗じる係数で、x1 = +の場合、他の変数のレベル内では、元の尺度での算術平均がx1 = -に比べて1.13倍になる。
また、指数化された切片 は、すべての予測変数で-となったウェハの算術平均結果である。
したがって、このモデルは、予測変数による元の結果への乗算効果を仮定している。
相違点と類似点
これらの2つのモデルは非常によく似ており、今回のケースでも似たような係数を出している、指数化された係数は異なる解釈をしている（幾何学的「平均比」と算術的「平均比」）。
これは
(対数スケールの平均は、元のスケールの平均の対数とは等しくない)
このように、線形回帰モデルに入る前に結果が対数変換されていれば、幾何平均に関する推論が可能となります。一方、一般化線形モデルのアプローチでは、元の尺度での算術平均についての推論が可能である。
いずれの場合も，各予測変数の効果は乗法的である（平均の変化率）。
代替案2 ガンマ・ファミリと同一性リンクを持つ一般化線形モデル（加法的算術平均モデル）
res.glm.Gamma.identity <- glm(formula = resist ~ x1 + x2 + x3 + x4,
family = Gamma(link = "identity"),
data = wafer)
summary(res.glm.Gamma.identity)
Call:
glm(formula = resist ~ x1 + x2 + x3 + x4, family = Gamma(link = "identity"),
data = wafer)
Deviance Residuals:
Min 1Q Median 3Q Max
-0.190394 -0.066533 0.005538 0.091549 0.126838
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 235.43 14.21 16.572 3.97e-09 ***
x1+ 27.83 12.24 2.274 0.044017 *
x2+ -65.74 12.68 -5.184 0.000302 ***
x3+ 36.94 12.32 2.999 0.012102 *
x4+ -11.88 12.15 -0.978 0.349294
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for Gamma family taken to be 0.0124071)
Null deviance: 0.69784 on 15 degrees of freedom
Residual deviance: 0.14009 on 11 degrees of freedom
AIC: 154.84
Number of Fisher Scoring iterations: 6
各予測変数の効果が元の尺度上で相加的であると考えられる場合，同一性リンク関数を持つ一般化線形モデルを使用できる。
この場合、生の係数は元の尺度になる。x1 = +を持つことは、算術平均の結果に27.83を加える（加法的効果）。
生の切片（235.43）は、すべての予測変数について-を有するウェーハの算術平均結果である。
