HardinとHilbeのStata本にあるベイジアンロジスティック回帰分析の続き。今回は事前分布としてコーシー分布を使う方法についてである。

Generalized Linear Models and Extensions: Fourth Edition
- 作者: James W. Hardin,Joseph M. Hilbe
- 出版社/メーカー: Stata Press
- 発売日: 2018/06/28
- メディア: ペーパーバック
- この商品を含むブログを見る
情報事前分布
先の2つのエントリーでは無情報事前分布(non-informative prior distribution)を用いてきたが、今回は情報事前分布(informative priors)を利用する。
センタリングした変数は医師の訪問cdocと年齢cageの2つで、この2つの変数をコーシー事前分布(Cauchy priors)を用いて推定する。ベイズ事前分布は堅実な外部情報に基づいている必要がある。ベイズ推定のように、既に同じようなものを計測していると、より確かな推定値が得られる。コーシー分布が堅実だと言い切れるかというとそうではない。実際に推定して推定結果を比較してどちらが良いか、比較することになる。
下記のケースでは推定の際に、任意の値をspecificationととして用いることで、デフォルトとは異なる推定を行う。 コーシー分布の理論的な説明は後ほどするとして、先にStataでの使用方法について述べていこう。
コーシー分布をベイジアンロジスティック回帰
Stata15以降の機能である。
. bayes,
> prior({outwork:female kids _cons}, normal(0, 1000))
> prior({outwork:cdoc}, cauchy(0,6))
> prior({outwork:cage}, cauchy(0,11))
> rseed (35841): glm outwork female kids cdoc cage, family(binomial)
Model summary
------------------------------------------------------------------------------
Likelihood:
outwork ~ glm(xb_outwork)
Priors:
{outwork:female kids _cons} ~ normal(0,1000) (1)
{outwork:cdoc} ~ cauchy(0,6) (1)
{outwork:cage} ~ cauchy(0,11) (1)
------------------------------------------------------------------------------
(1) Parameters are elements of the linear form xb_outwork.
Bayesian generalized linear models MCMC iterations = 12,500
Random-walk Metropolis-Hastings sampling Burn-in = 2,500
MCMC sample size = 10,000
Family : Bernoulli Number of obs = 3,874
Link : logit Scale parameter = 1
Acceptance rate = .2057
Efficiency: min = .03496
avg = .04486
Log marginal-likelihood = -1993.0855 max = .05717
------------------------------------------------------------------------------
| Equal-tailed
outwork | Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
female | 2.260141 .0842407 .004506 2.254865 2.097708 2.431913
kids | .3540421 .0906731 .003792 .3560368 .1811122 .5379961
cdoc | .0248758 .0063243 .000318 .0247956 .0130655 .0382379
cage | .0544032 .0039354 .00017 .0543025 .0469003 .0626092
_cons | -2.012612 .0799112 .004051 -2.011676 -2.171733 -1.862155
------------------------------------------------------------------------------
コーシー分布を事前分布ベイジアンロジスティック回帰・MH法
同じく、Stata15以降の機能である。
. bayesmh outwork female kids cdoc cage, likelihood (logit)
> prior({outwork:female kids _cons}, normal(0, 1000))
> prior({outwork:cdoc}, cauchy(0,6))
> prior({outwork:cage}, cauchy(0,11))
> rseed (35841)
Model summary
------------------------------------------------------------------------------
Likelihood:
outwork ~ logit(xb_outwork)
Priors:
{outwork:female kids _cons} ~ normal(0,1000) (1)
{outwork:cdoc} ~ cauchy(0,6) (1)
{outwork:cage} ~ cauchy(0,11) (1)
------------------------------------------------------------------------------
(1) Parameters are elements of the linear form xb_outwork.
Bayesian logistic regression MCMC iterations = 12,500
Random-walk Metropolis-Hastings sampling Burn-in = 2,500
MCMC sample size = 10,000
Number of obs = 3,874
Acceptance rate = .1844
Efficiency: min = .03402
avg = .05568
Log marginal-likelihood = -1993.0309 max = .07315
------------------------------------------------------------------------------
| Equal-tailed
outwork | Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
female | 2.258607 .0839686 .004552 2.261023 2.0928 2.423481
kids | .3565683 .0899923 .003727 .3605532 .1768716 .5279933
cdoc | .024811 .0064852 .000282 .0244694 .0122816 .0378834
cage | .0547071 .0039411 .000146 .0547988 .0469502 .06197
_cons | -2.010109 .0794933 .003246 -2.009283 -2.171436 -1.854177
------------------------------------------------------------------------------
情報基準量
情報基準量はいつもの通り。
. bayesstats ic
Bayesian information criteria
----------------------------------------------
| DIC log(ML) log(BF)
-------------+--------------------------------
active | 3928.181 -1993.031 .
----------------------------------------------
Note: Marginal likelihood (ML) is computed
using Laplace-Metropolis approximation.
分布の比較
無情報事前分布(noninformative)とコーシー分布(informative)を用いた推定値の比較をしてみよう。
| noninformative | informative | |
|---|---|---|
| female | 2.60 | 2.259 |
| kids | 0.356 | 0.356 |
| cdoc | 0.024 | 0.025 |
| cage | 0.055 | 0.055 |
| xcons | -2.01 | -2.01 |
Stataにはモデルの事後確率を基に仮説検定ができるコマンドがあるとのこと。bayestest modelコマンドを利用すると、モデルの限界尤度と事前確率と事後確率が表示できるようだ。レファレンスを参照とのこと。
プロット
cageのグラフに改善点があったため、それが前回の推定より改善されているかが問題となる。改善をしていれば、コーシー事前分布は有用ということになる。
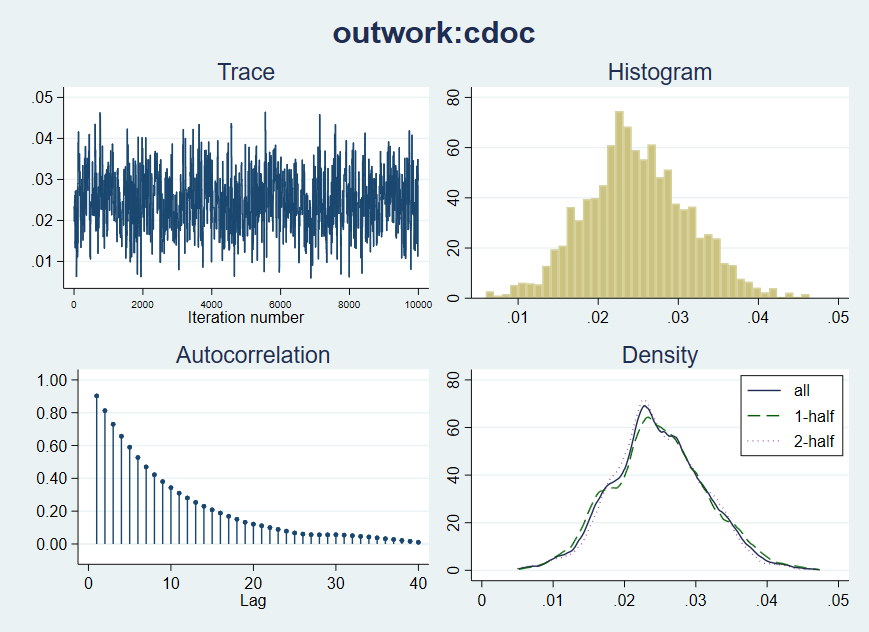
. bayesgraph diagnostics {outwork:cdoc}
. bayesgraph diagnostics {outwork:cage}
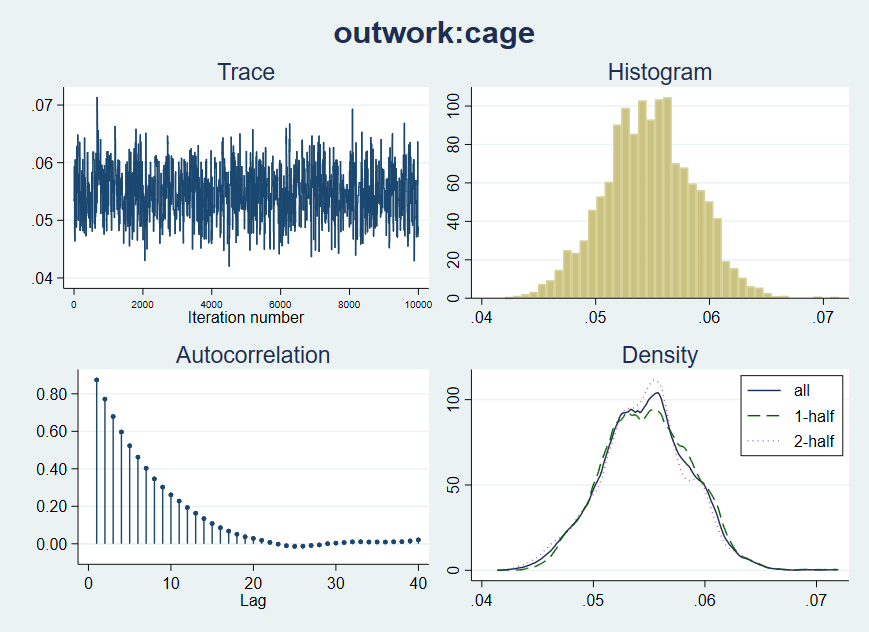
このグラフは以前よりも改善されている。センタリングされた年齢の変数は以前のグラフではほぼ二峰性だった(参照)。 また、このモデルでは、無情報事前分布のモデルよりもcageの確信区間が狭くなっている。その理由は事前確率があった方が情報量がわずかに多いためである。Cauchy事前分布のモデルは、フラット事前分布のモデルよりも、センタリングされた年齢変数に適したものになっている。
コーシー分布
コーシー事前分布では、位置パラメーターとスケールパラメーター指定する。
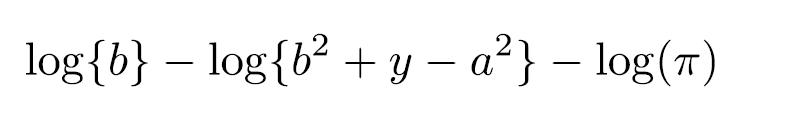
上の式をStataのコマンドにすると以下のようになる。
prior({outwork: cage}, logdensity(ln(11)-ln(11^2+({outwork: cage})^2-ln(_pi))))
Stata15から導入されたprefixであるcauchy()はこの式をlogdensity()オプションに入れなくてもコマンドを走らせることができる。
ベイズ統計でコーシー分布といえばGelmanの論文である。
projecteuclid.org
PDF
http://www.stat.columbia.edu/~gelman/research/published/taumain.pdf
本としては以下のもの。

Bayesian Data Analysis (Chapman & Hall/CRC Texts in Statistical Science)
- 作者: Andrew Gelman,John B. Carlin,Hal S. Stern,David B. Dunson,Aki Vehtari,Donald B. Rubin
- 出版社/メーカー: Chapman and Hall/CRC
- 発売日: 2013/11/05
- メディア: ハードカバー
- この商品を含むブログを見る
コーシー分布を事前分布としたベイジアンロジスティック回帰
logdensity()のオプション指定をすると、Stata15から搭載されたcauchy()のprefixを使わずに、同様の意味を持つ式が書けるのでStata14でも走るように思うのだが、Stata14は持ってないのでよくわからない。
変数cdocおよびcageについては、a = 0を設定する。cdocはscaleパラメーターb = 6を設定し、cageはb = 11とする。説明が前後しているが、これらの任意の値は冒頭のスクリプトにも入れてある。変数femaleとkidsはnormal(0,1000)の事前分布を使用。これはベイズ統計を使用するときのデフォルトである。
スクリプトは次のようになる。
. bayes, prior({outwork:female kids _cons}, normal(0, 1000))
> prior({outwork:cdoc},
> logdensity(ln(6)-ln(6^2+({outwork:cdoc})^2)-ln(_pi)))
> prior({outwork:cage},
> logdensity(ln(11)-ln(11^2+{outwork:cage}^2)-ln(_pi)))
> rseed (35841): glm outwork female kids cdoc cage, family(binomial)
コーシー分布を事前分布としたベイジアンロジスティック回帰・MH法
MH法のbayesmhコマンドでは次のように指定する。
. bayesmh outwork female kids cdoc cage, likelihood(logit)
> prior({outwork:female kids _cons}, normal(0, 1000))
> prior({outwork:cdoc},
> logdensity(ln(6)-ln(6^2+({outwork:cdoc})^2)-ln(_pi)))
> prior({outwork:cage},
> logdensity(ln(11)-ln(11^2+({outwork:cage})^2)-ln(_pi)))
> rseed (35841)
logdensity()でコーシー分布の指定をしなくてもいいので、Stata15以降の方が多少楽になった気はする。
HardinとHilbeのテキストのコーシー分布自力計算のスクリプト内logdensity()オプションの中に誤植があったので、教科書を書く人間が間違うくらいだから、Stata15以降の改善は良いことなのだろうと思う。