順序ロジスティック回帰[R] - 井出草平の研究ノート

idreの解説より。

stats.idre.ucla.edu

後半記載されているparallel slopesの検定だが、現在はbrantパッケージでできるのではないかと思う。そのうちエントリをいれるつもり。

はじめに

このページでは、Rのporrパッケージを使って順序ロジスティック回帰を行う方法を説明する。結果の解釈についてのより数学的な取り扱いについては、以下を参照。 https://stats.idre.ucla.edu/r/faq/ologit-coefficients/

準備

このページの例題を実行する前に、以下のパッケージがロードできることを確認する。パッケージがインストールされていない場合は、install.packages("packagename")を、バージョンが古い場合は、update.packages()を実行する。

require(foreign)
require(ggplot2)
require(MASS)
require(Hmisc)
require(reshape2)

順序ロジスティック回帰の例

例1: あるマーケティング・リサーチ会社が、ファーストフード・チェーン店で人々が注文するソーダのサイズ（スモール、ミディアム、ラージ、エクストララージ）に影響を与える要因を調査したいと考えている。これらの要因には、注文したサンドイッチの種類（ハンバーガーまたはチキン）、フライドポテトを注文するかどうか、消費者の年齢などがある。結果変数であるソーダのサイズは明らかに注文されていますが、様々なサイズ間の差は一貫していない。smallとmediumの差は10オンス、mediumとlargeの差は8オンス、largeとextra largeの差は12オンスとなっている。

例2：ある研究者は、オリンピックの水泳でメダル獲得に影響を与える要因は何かに興味を持っている。関連する予測因子には、トレーニング時間、食事、年齢、アスリートの母国での水泳人気などがある。研究者は、金メダルと銀メダルの間の距離は、銀メダルと銅メダルの間の距離よりも大きいと考えている。

例3：ある研究では、大学院に出願するかどうかの判断に影響を与える要因を調べている。大学3年生に、大学院に出願する可能性が低いか、やや高いか、非常に高いかを尋ねる。したがって、結果変数は3つのカテゴリーになる。また、親の教育状況、学部が公立か私立か、現在のGPAなどのデータも収集している。この3つのポイント間の「距離」は等しくないと研究者は考えている。例えば、「可能性が低い」と「やや可能性が高い」の間の「距離」は、「やや可能性が高い」と「非常に可能性が高い」の間の距離よりも短いかもしれない。

データの説明

以下のデータ分析では、大学院への出願に関する例3を拡大して説明する。この例のためにいくつかのデータをシミュレートしており、それは当社のウェブサイトから入手できる。

dat <- read.dta("https://stats.idre.ucla.edu/stat/data/ologit.dta")
head(dat)

            apply pared public  gpa
1     very likely     0      0 3.26
2 somewhat likely     1      0 3.21
3        unlikely     1      1 3.94
4 somewhat likely     0      0 2.81
5 somewhat likely     0      0 2.53
6        unlikely     0      1 2.59

この仮想データセットには、"apply "という3段階の変数があり、"unlikely"、"therely likely"、"very likely"の3段階で、それぞれ1、2、3とコードされており、これを結果変数として使用する。また、予測変数として、pared（親のうち少なくとも一人が大学院卒であることを示す0/1の変数）、public（学部が公立であることを示す1、私立であることを示す0の0/1の変数）、gpa（学生の成績平均値）の3つの変数を用意した。まず、これらの変数の記述統計を見てみよう。

lapply(dat[, c("apply", "pared", "public")], table)

$apply

       unlikely somewhat likely     very likely 
            220             140              40 

$pared

  0   1 
337  63 

$public

  0   1 
343  57

ftable(xtabs(~ public + apply + pared, data = dat))

                       pared   0   1
public apply                        
0      unlikely              175  14
       somewhat likely        98  26
       very likely            20  10
1      unlikely               25   6
       somewhat likely        12   4
       very likely             7   3

summary(dat$gpa)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.900   2.720   2.990   2.999   3.270   4.000

sd(dat$gpa)

[1] 0.3979409

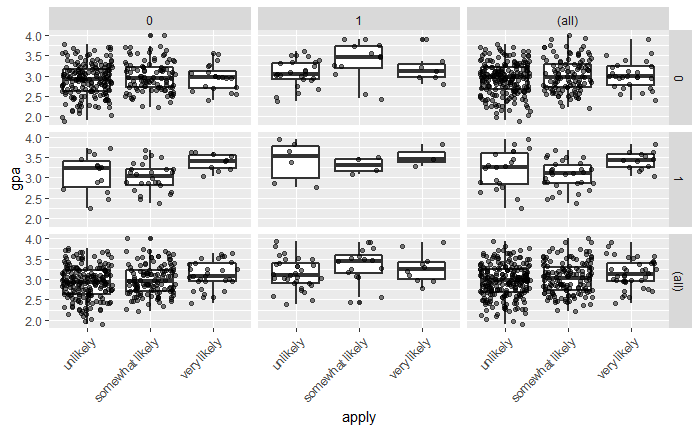
また、応募レベルごとの成績評価の分布を、公開度と公開度に分けて調べることもできる。これにより、2×2のグリッドに、「pared」と「public」の特定の値について、「apply」の各レベルの成績を箱ひげ図にしている。データを見やすくするために、箱ひげ図の上に生のデータポイントを追加た。箱ひげ図を圧倒しないように、少量のノイズ（しばしば「ジッター」と呼ばれます）と50％の透明度を加えました。最後に、セルに加えて、すべてのマージナル関係をプロットする。余白があることで、最終的に3×3のグリッドができあがる。右下にあるのは、「応募」と「成績」の全体的な関係で、わずかに正の値を示している。これには ggplot2 パッケージを使う。

ggplot(dat, aes(x = apply, y = gpa)) +
  geom_boxplot(size = .75) +
  geom_jitter(alpha = .5) +
  facet_grid(pared ~ public, margins = TRUE) +
  theme(axis.text.x = element_text(angle = 45, hjust = 1, vjust = 1))

f:id:iDES:20210717041720p:plain

想定される解析方法

ここでは、皆様が遭遇したことのある分析方法をいくつか紹介する。ここに挙げた方法の中には非常に合理的なものもあれば、廃れてしまったものや限界のあるものもある。

順序付きロジスティック回帰：このページの焦点である。
OLS回帰です。この分析は、非楕円形の結果変数で使用される場合、OLSの仮定が破られるので問題があります。
ANOVA: 1つの連続予測変数のみを使用する場合、モデルを「反転」させて、たとえば、gpaが結果変数で、applyが予測変数になるようにすることができます。そして、一元配置のANOVAを実行することができるこれは、（ロジスティック・モデルからの）予測変数が1つだけで、それが連続的である場合には、悪いことではない。
多項ロジスティック回帰。これは，結果変数のカテゴリに順序がない（すなわち，カテゴリが名目的である）と仮定されることを除いて，順序付きロジスティック回帰を行うことに似ている。このアプローチの欠点は、順序に含まれる情報が失われることである。
順序付きプロビット回帰。これは、順序付きロジスティック回帰を実行するのと非常によく似ています。主な違いは、係数の解釈にある。

順序ロジスティック回帰

以下では、MASSパッケージのporrコマンドを使って、順序付きロジスティック回帰モデルを推定する。このコマンド名は、比例オッズ・ロジスティック回帰に由来しており、このモデルにおける比例オッズの仮定を強調している。また、Hess=TRUEを指定することで、モデルが最適化により観測された情報行列（ヘシアンHessianと呼ばれる）を返し、標準誤差を得るために使用される。

定義

係数の解釈方法を理解するために、まずいくつかの表記法を確立し、順序ロジスティック回帰に関連する概念を確認しましょう。 $Y$ を $J$ 個のカテゴリを持つ順序結果とする．そして， $P(Y{\leq}j)$ は， $Y$ が特定のカテゴリ $j = 1, ...m J-1$ 以下である累積確率である．特定のカテゴリ以下であることのオッズは、次のように定義できる。

$\frac{P(Y{\leq}1)}{P(Y>j)}$

$j=1, ..., J-1$ で $P(Y>J)$ であり、ゼロで割るのは不定である。対数オッズはロジットとも呼ばれる。

$log\frac{P(Y{\leq}j)}{P(Y>j)}=logit(P(Y{\leq}j)).$

Rのpolrでは、順序ロジスティック回帰モデルは次のようにパラメータ化される。

$logit(P(Y{\leq}j))=\beta_{j0}-{\eta_1}{x_1}-...-{\eta_p}{x_p}.$

そして、次のような順序ロジスティック回帰モードに適合させることができる。

## fit ordered logit model and store results 'm'
m <- polr(apply ~ pared + public + gpa, data = dat, Hess=TRUE)

## view a summary of the model
summary(m)

Call:
polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE)

Coefficients:
          Value Std. Error t value
pared   1.04769     0.2658  3.9418
public -0.05879     0.2979 -0.1974
gpa     0.61594     0.2606  2.3632

Intercepts:
                            Value   Std. Error t value
unlikely|somewhat likely     2.2039  0.7795     2.8272
somewhat likely|very likely  4.2994  0.8043     5.3453

Residual Deviance: 717.0249 
AIC: 727.0249

推定モデルは次のように書くことができる。

$logit(\hat{P}(Y{\leq}1)) = 2.20 - 1.05*PARED - (-0.06)*PUBLIC - 0.616*GPA$
$logit(\hat{P}(Y{\leq}2)) = 4.30 - 1.05*PARED - (-0.06)*PUBLIC - 0.616*GPA$

上の出力では、次のようになっている。

これはRが、実行したモデルの種類や指定したオプションなどを思い出させてくれるものである。
次に、各係数の値、標準誤差、t値（単純に係数とその標準誤差の比）を含む通常の回帰出力係数表が表示される。デフォルトでは有意差検定はない。
次に、カットポイントとも呼ばれる2つの切片の推定値が表示される。切片は、データで観察される3つのグループを作るために潜在変数がどこでカットされるかを示す。この潜在変数は連続であることに注意。一般的に、これらは結果の解釈には使用されない。カットポイントは、他の統計パッケージで報告されるしきい値と密接に関連している。
最後に、モデルの残差分散、-2 * Log Likelihood、およびAICが表示されます。残差分散とAICは、モデルの比較に役立つ。

p値がないと満足できない人もいます。この場合、p値を計算する一つの方法は、z検定のように、t値を標準正規分布と比較することである。もちろん、これは自由度が無限にある場合にのみ当てはまりますが、大きなサンプルでは合理的に近似され、サンプルサイズが小さくなるとますます偏りが大きくなる。この方法は、Stataなどの他のソフトウェアパッケージでも使用されており、簡単に行うことができる。まず、係数表を保存し、次にp値を計算して表に戻す。

## store table
(ctable <- coef(summary(m)))

                                  Value Std. Error    t value
pared                        1.04769010  0.2657894  3.9418050
public                      -0.05878572  0.2978614 -0.1973593
gpa                          0.61594057  0.2606340  2.3632399
unlikely|somewhat likely     2.20391473  0.7795455  2.8271792
somewhat likely|very likely  4.29936315  0.8043267  5.3452947

## calculate and store p values
p <- pnorm(abs(ctable[, "t value"]), lower.tail = FALSE) * 2

## combined table
(ctable <- cbind(ctable, "p value" = p))

                                  Value Std. Error    t value      p value
pared                        1.04769010  0.2657894  3.9418050 8.087072e-05
public                      -0.05878572  0.2978614 -0.1973593 8.435464e-01
gpa                          0.61594057  0.2606340  2.3632399 1.811594e-02
unlikely|somewhat likely     2.20391473  0.7795455  2.8271792 4.696004e-03
somewhat likely|very likely  4.29936315  0.8043267  5.3452947 9.027008e-08

また、パラメータ推定値の信頼区間を得ることもできる。これらは、尤度関数をプロファイリングするか、標準誤差を使用して正規分布を仮定することで得られる。プロファイリングされたCIは対称ではないことに注意（通常は対称に近いが）。95% CIが0と交差しない場合、パラメータ推定値は統計的に有意である。

(ci <- confint(m)) # default method gives profiled CIs

            2.5 %    97.5 %
pared   0.5281768 1.5721750
public -0.6522060 0.5191384
gpa     0.1076202 1.1309148

confint.default(m) # CIs assuming normality

            2.5 %    97.5 %
pared   0.5267524 1.5686278
public -0.6425833 0.5250119
gpa     0.1051074 1.1267737

paredとgpaのCIには0が含まれていない、publicには含まれている。出力の推定値は、順序付きロジット（順序付き対数オッズ）の単位で与えられる。paredについては、モデル内の他のすべての変数を一定とした場合、paredが1単位増加する（つまり、0から1になる）と、対数オッズスケールでの適用の期待値が1.05増加すると予想される。gpaについては、モデル内の他のすべての変数を一定とした場合、gpaが1単位増加すると、対数オッズスケールでの「応募」の期待値が0.62増加すると予想される。

このモデルの係数は、対数でスケールされているので、解釈がやや難しいかもしれない。ロジスティック回帰モデルを解釈する別の方法は、係数をオッズ比に変換することである。ORと信頼区間を得るには、推定値と信頼区間を指数化するだけである。

## odds ratios
exp(coef(m))

    pared    public       gpa 
2.8510579 0.9429088 1.8513972

## OR and CI
exp(cbind(OR = coef(m), ci))

              OR     2.5 %   97.5 %
pared  2.8510579 1.6958376 4.817114
public 0.9429088 0.5208954 1.680579
gpa    1.8513972 1.1136247 3.098490

これらの係数は比例オッズ比と呼ばれ、二値ロジスティック回帰のオッズ比とほぼ同じように解釈する。

オッズ比の解釈

確率の定義方法とオッズの方向性に基づいて、オッズ比には多くの同等の解釈がある。詳細な説明については下記を参照。 https://stats.idre.ucla.edu/r/faq/ologit-coefficients/

以下の(*)記号は、選択肢の中で最も簡単な解釈を示している。

親の教育

(*) 両親が大学に通っている学生は、他のすべての変数を一定にした場合、両親が大学に通っていない学生に比べて、応募する可能性が高い（非常に高い、またはやや高い対低い）オッズが2.85倍になる。
両親が大学に通っていない学生の場合、出願する可能性が低い（つまり、可能性が低い対やや高い、または非常に高い）オッズは、他のすべての変数を一定にして、両親が大学に通っている学生の2.85倍になる。

学校の種類

公立学校の生徒は、私立学校の生徒に比べて、他のすべての変数を同じにしても、応募する可能性が高い（つまり、非常にまたはやや高い可能性と低い可能性）オッズは5.71％低い（つまり、（1 -0.943）×100％）。
(*) 私立学校の生徒は、他のすべての変数を一定とした場合、公立学校の生徒の1.06倍[すなわち、1/0.943]の応募可能性がある（正のオッズ比）。
私立学校の生徒の場合、他のすべての変数を同じにして、応募する可能性が低い（つまり、可能性が低いと思うか、やや可能性が高いか、非常に可能性が高いか）確率は、公立学校の生徒よりも5.71%低い。
公立学校の生徒の場合、他のすべての変数を一定とした場合、応募する可能性が低いというオッズは、私立学校の生徒の1.06倍になる（正のオッズ比）。

GPA

(*) 学生のGPAが1単位増加するごとに、他のすべての変数を一定にしたまま、応募する可能性が高くなる確率（非常にまたはやや高い可能性と低い可能性）が1.85倍になる（つまり、85％増加）。
学生のGPAが1単位下がるごとに、応募する可能性が低くなる確率（可能性が低いとやや高い、または非常に高い）は、他のすべての変数を一定にして、1.85倍になる。

比例オッズの仮定

順序ロジスティック（および順序プロビット）回帰の基礎となる仮定の1つは，結果グループの各ペアの間の関係が同じであることである．言い換えると，順序ロジスティック回帰は，たとえば，応答変数の最も低いカテゴリとすべての高いカテゴリの間の関係を記述する係数が，次に低いカテゴリとすべての高いカテゴリの間の関係を記述する係数と同じであることを仮定する。これは、比例オッズの仮定または平行回帰の仮定と呼ばれています。すべてのグループのペアの間の関係は同じなので、係数のセットは1つだけである。

もしそうでなければ、結果グループの各ペア間の関係を記述するために、モデル内に異なる係数のセットが必要になる。したがって、モデルの妥当性を評価するためには、比例オッズの仮定が有効であるかどうかを評価する必要がある。これを行うための統計的検定は、いくつかのソフトウェアパッケージで提供されている。しかし、これらの検定は、帰無仮説（係数のセットが同じであるという）を棄却する傾向があり、したがって、平行スロープparallel slopesの仮定が成り立つ場合には、その仮定が成り立たないことを示していると批判されている（Harrell 2001 p.335参照）。平行スロープの仮定を検証するために一般的に使用されるテストを実行する機能をRで見つけることができなかった。しかし、Harrellは平行スロープの仮定を評価するためのグラフ手法を推奨している。このグラフに表示されている値は、基本的にロジットモデルからの（線形）予測値であり、予測変数（x）を一度に1つ使用して、yが（yの各レベルについて）与えられた値以上である確率をモデルするために使用される。このグラフを作成するには、Hmiscライブラリが必要である。

以下のコードには2つのコマンドが含まれており（最初のコマンドは複数行に分かれています）、比例オッズの仮定を検証するためにこのグラフを作成するのに使用するします。基本的に、我々は、結果グループが apply >= 2 と apply >= 3のどちらかで定義される単一の予測変数を持つ個々のロジスティック回帰からの予測されたロジットをグラフ化する。予測変数のさまざまなレベル、たとえばparedの予測されたロジットの差が、結果が apply >= 2 または apply >= 3で定義されるかどうかにかかわらず同じであれば、我々は比例オッズ仮定が成り立つことを確信できる。言い換えれば、pared = 0 と pared = 1 のロジットの差が、結果が apply >= 2 のときの差と apply >= 3 のときの差が同じであれば、比例オッズの仮定が成り立つ可能性が高いということである。

最初のコマンドは、グラフ化される値を推定する関数を作成する。このコマンドの最初の行では、Rにsfが関数であること、この関数がyというラベルのついた1つの引数を取ることを伝えている。sf関数は、対象となる変数の各値よりも大きいか等しいかの対数オッズを計算する。我々の目的では、2以上に適用される対数オッズと3以上に適用される対数オッズを求める。従属変数のカテゴリの数や変数のコーディングによっては、この関数を編集する必要があるかもしれない。下記の関数は、1, 2, 3の3つのレベルを持つy変数のために構成されている。従属変数が1, 2, 3, 4という4つのレベルを持つ場合、'Y>=4'=qlogis(mean(y >= 4)) を追加する必要がある。引用符を除いて）最初の括弧の中に追加する必要がある。従属変数のコードが1, 2, 3ではなく0, 1, 2だった場合は、コードを編集して、1の各インスタンスを0に、2を1に、というように置き換える必要があります。sf関数の中には、確率をロジットに変換するqlogis関数がある。つまり、基本的には、適用される確率が2や3よりも大きいことをqlogisに与え、これらの確率のロジット変換を返す。qlogis関数の内部では、y >= 2の平均の対数オッズが必要であることがわかる。関数 sf に apply のような y 引数を与えると、y >= 2 は 0/1 (FALSE/TRUE) のベクトルに評価され、そのベクトルの平均を取ることで apply >= 2 の割合または確率が得られる。

以下の2つ目のコマンドは、予測因子によって定義されたデータのいくつかのサブセットに対して、関数sfを呼び出します。このステートメントでは、最初の引数として式が与えられたsummary関数が見られる。Rは、数式の引数を持つsummaryの呼び出しを見ると、数式の右側のグループによる数式の左側の変数の記述統計量を計算し、その結果をきれいな表にして返す。デフォルトでは、summary は左辺の変数の平均を計算します。つまり、summary(as.numeric(apply) ~ pared + public + gpa) というコードを fun 引数なしで使用した場合、apply を pared で、次に public で、最後に gpa で 4 等分した平均値を得ることができる。しかし、独自の関数、つまりsfをfun=引数に与えることで、平均値の計算を上書きすることができます。最後のコマンドは、Rにオブジェクトsの内容を返すように要求するが、それはテーブルです。

sf <- function(y) {
  c('Y>=1' = qlogis(mean(y >= 1)),
    'Y>=2' = qlogis(mean(y >= 2)),
    'Y>=3' = qlogis(mean(y >= 3)))
}

(s <- with(dat, summary(as.numeric(apply) ~ pared + public + gpa, fun=sf)))

as.numeric(apply)     N= 400 

+-------+-----------+---+----+-----------+---------+
|       |           |  N|Y>=1|       Y>=2|     Y>=3|
+-------+-----------+---+----+-----------+---------+
|  pared|         No|337| Inf|-0.37833644|-2.440735|
|       |        Yes| 63| Inf| 0.76546784|-1.347074|
+-------+-----------+---+----+-----------+---------+
| public|         No|343| Inf|-0.20479441|-2.345006|
|       |        Yes| 57| Inf|-0.17589067|-1.547563|
+-------+-----------+---+----+-----------+---------+
|    gpa|[1.90,2.73)|102| Inf|-0.39730180|-2.772589|
|       |[2.73,3.00)| 99| Inf|-0.26415158|-2.302585|
|       |[3.00,3.28)|100| Inf|-0.20067070|-2.090741|
|       |[3.28,4.00]| 99| Inf| 0.06062462|-1.803594|
+-------+-----------+---+----+-----------+---------+
|Overall|           |400| Inf|-0.20067070|-2.197225|
+-------+-----------+---+----+-----------+---------+

上の表は、平行スロープの仮定なしで、従属変数を予測変数に1回ずつ回帰した場合に得られる（線形）予測値を表示ている。我々は、従属変数のカットポイントを変えて一連のバイナリ・ロジスティック回帰を実行して、カットポイント間での係数の等質性をチェックすることで、平行スロープの仮定を評価できる。そこで、平行スロープの仮定を緩和して、その妥当性を確認します。これを達成するために、我々は、元の順序従属変数を、元の順序従属変数（ここでは適用）がある値aより小さい場合は0に、順序変数がa以上の場合は1に等しい、新しい、バイナリの従属変数に変換する（これは、順序回帰モデルの係数も同様に表すものであることに注意）。これは、順序変数のk-1レベルに対して行われ、以下のas.numeric(apply) >= aのコーディングによって実行される1行目のコードでは、「可能性が低い」を選択した場合と「やや可能性が高い」「非常に可能性が高い」を選択した場合のparedの効果を推定しています。2行目のコードは、"可能性が低い "または "やや可能性が高い "を選択した場合と "非常に可能性が高い "を選択した場合のparedの効果を推定しています。このモデルの切片（-0.3783）を見ると、Y>=1の列でparedが「no」に等しい場合のセルの予測値と一致し、その下のparedが「yes」に等しい場合の値は、切片にparedの係数を加えたもの（すなわち、-0.3783 + 1.1438 = 0.765）になる。

glm(I(as.numeric(apply) >= 2) ~ pared, family="binomial", data = dat)

Call:  glm(formula = I(as.numeric(apply) >= 2) ~ pared, family = "binomial", 
    data = dat)

Coefficients:
(Intercept)        pared  
    -0.3783       1.1438  

Degrees of Freedom: 399 Total (i.e. Null);  398 Residual
Null Deviance:      550.5 
Residual Deviance: 534.1    AIC: 538.1

glm(I(as.numeric(apply) >= 3) ~ pared, family="binomial", data = dat)

Call:  glm(formula = I(as.numeric(apply) >= 3) ~ pared, family = "binomial", 
    data = dat)

Coefficients:
(Intercept)        pared  
     -2.441        1.094  

Degrees of Freedom: 399 Total (i.e. Null);  398 Residual
Null Deviance:      260.1 
Residual Deviance: 252.2    AIC: 256.2

この表の値を使って、比例オッズの仮定がこのモデルにとって妥当かどうかを評価することができる。(例えば、paredが "no "に等しい場合、2以上の適用と3以上の適用の予測値の間の差は、およそ2である（-0.378 - -2.440 = 2.062）。paredが「はい」の場合、「2以上の適用」と「3以上の適用」の予測値の差もおおよそ2（0.765 - -1.347 = 2.112）となる。このことから、平行勾配の仮定が妥当であることがわかる（下のグラフは、この差をプロットしたものである）。publicを予測変数とした場合の予測に目を向けると、publicを「no」に設定した場合、「2以上の適用」と「3以上の適用」の予測の差は約2.14(-0.204 - - 2.345 = 2.141)となる。公開を「はい」に設定した場合、係数の差は約1.37（-0.175 - -1.547 = 1.372）となる。2組の係数の距離の違い（2.14 vs. 1.37）は、予測変数publicに対して平行勾配の仮定が成り立たないことを示唆しているのかもしれない。これは、"可能性は低い "から "やや可能性が高い"への移行と "やや可能性が高い "から "非常に可能性が高い "への移行において、公立学校と私立学校への通学の効果が異なることを示している。

以下のplotコマンドは、プロットしたい対象がsであることをRに伝える。which=1:3コマンドは、プロットに含まれるべきyのレベルを示す値のリストである。従属変数が3つ以上のレベルを持つ場合は、3をカテゴリーの数に変更する必要がある（例えば、4つのカテゴリー変数の場合は、0, 1, 2, 3と番号が付いていても4とする）。コマンドpch=1:3は、使用するマーカーを選択し、x軸をラベル付けするxlab='logit'や、グラフのメインラベルを空白にするmain=' ' と同様にオプションです。比例オッズの仮定が成り立つなら、各予測変数について、従属変数のカテゴリの各セットのシンボル間の距離は、同じようになるはずである。このことを示すために、共通の基準点があるように、最初のセットの係数をすべてゼロに正規化した。pared という変数の係数を見ると、2つの係数セットの間の距離が似ていることがわかる。これとは対照的に、publicの推定値の間の距離は異なっており（つまり、1行目よりも2行目の方がマーカーが大きく離れている）、比例オッズの仮定が成り立たない可能性を示唆している。

s[, 4] <- s[, 4] - s[, 3]
s[, 3] <- s[, 3] - s[, 3]
s # print

as.numeric(apply)     N= 400 

+-------+-----------+---+----+----+---------+
|       |           |  N|Y>=1|Y>=2|     Y>=3|
+-------+-----------+---+----+----+---------+
|  pared|         No|337| Inf|   0|-2.062399|
|       |        Yes| 63| Inf|   0|-2.112541|
+-------+-----------+---+----+----+---------+
| public|         No|343| Inf|   0|-2.140211|
|       |        Yes| 57| Inf|   0|-1.371672|
+-------+-----------+---+----+----+---------+
|    gpa|[1.90,2.73)|102| Inf|   0|-2.375287|
|       |[2.73,3.00)| 99| Inf|   0|-2.038434|
|       |[3.00,3.28)|100| Inf|   0|-1.890070|
|       |[3.28,4.00]| 99| Inf|   0|-1.864219|
+-------+-----------+---+----+----+---------+
|Overall|           |400| Inf|   0|-1.996554|
+-------+-----------+---+----+----+---------+

plot(s, which=1:3, pch=1:3, xlab='logit', main=' ', xlim=range(s[,3:4]))

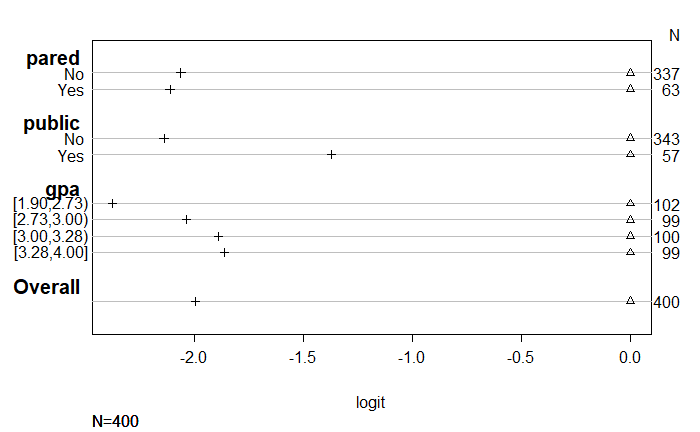
f:id:iDES:20210717041834p:plain

モデルの仮定が成り立つかどうかの評価が終わったら、予測される確率を得ることができる。これは通常、係数やオッズ比よりも理解しやすい。例えば、paredとpublicの各レベルでgpaを変化させ、それぞれのカテゴリーの応募者になる確率を計算する。このためには、予測に使用するすべての値の新しいデータセットを作成する。

newdat <- data.frame(
  pared = rep(0:1, 200),
  public = rep(0:1, each = 200),
  gpa = rep(seq(from = 1.9, to = 4, length.out = 100), 4))

newdat <- cbind(newdat, predict(m, newdat, type = "probs"))

##show first few rows
head(newdat)

  pared public      gpa  unlikely somewhat likely very likely
1     0      0 1.900000 0.7376186       0.2204577  0.04192370
2     1      0 1.921212 0.4932185       0.3945673  0.11221424
3     0      0 1.942424 0.7325300       0.2244841  0.04298593
4     1      0 1.963636 0.4866885       0.3984676  0.11484395
5     0      0 1.984848 0.7273792       0.2285470  0.04407383
6     1      0 2.006061 0.4801630       0.4023098  0.11752712

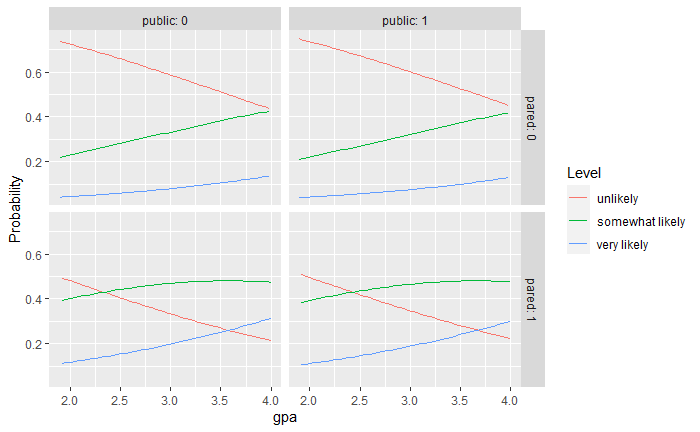
ここで、reshape2パッケージを使ってデータをリシェイプし、異なる条件での予測確率をすべてプロットする。予測された確率を線で結び、結果のレベル「apply」で色分けし、「pared」と「public」のレベルでファセットしてプロットする。また、カスタムラベル関数を使用して、プロットの各列と行が何を表しているかを示す明確なラベルを追加する。

lnewdat <- melt(newdat, id.vars = c("pared", "public", "gpa"),
  variable.name = "Level", value.name="Probability")
## view first few rows
head(lnewdat)

  pared public      gpa    Level Probability
1     0      0 1.900000 unlikely   0.7376186
2     1      0 1.921212 unlikely   0.4932185
3     0      0 1.942424 unlikely   0.7325300
4     1      0 1.963636 unlikely   0.4866885
5     0      0 1.984848 unlikely   0.7273792
6     1      0 2.006061 unlikely   0.4801630

ggplot(lnewdat, aes(x = gpa, y = Probability, colour = Level)) +
  geom_line() + facet_grid(pared ~ public, labeller="label_both")

f:id:iDES:20210717041800p:plain

考慮すべき点

完璧な予測：完全予測とは、予測変数の1つの値が応答変数の1つの値だけと関連することを意味する。このような場合、Stataは通常、出力の先頭に注意書きをし、モデルが実行できるようにケースを削除する。
サンプルサイズ：最尤推定法を用いた順序付きロジスティックと順序付きプロビットは、どちらも十分なサンプルサイズを必要とする。どの程度の大きさかは議論のあるところだが、ほとんどの場合、OLS回帰よりも多くのケースを必要とする。
空のセルまたは小さなセルけカテゴリカル予測変数と結果変数の間のクロスタブを行って、空のセルまたは小さなセルをチェックするべきである。セルにケースがほとんどない場合、モデルが不安定になるか、まったく実行されないかもしれない。
擬似R-2乗：OLSで見られるR-squaredの正確なアナログはない。疑似R2乗には多くのバージョンがある。様々な擬似R二乗の詳細と説明についてはLong and Freese 2005を参照。
診断：非線形モデルの診断を行うことは難しく、順序付きロジット/プロビット・モデルはバイナリ・モデルよりもさらに難しい。ロジスティック回帰のモデル診断の議論については、Hosmer and Lemeshow (2000, Chapter 5)を参照のこと。なお、ロジスティック回帰の診断は、プロビット回帰の診断と同様である。

References

Agresti, A. (1996) An Introduction to Categorical Data Analysis. New York: John Wiley & Sons, Inc
Agresti, A. (2002) Categorical Data Analysis, Second Edition. Hoboken, New Jersey: John Wiley & Sons, Inc.
Harrell, F. E, (2001) Regression Modeling Strategies. New York: Springer-Verlag.
Liao, T. F. (1994) Interpreting Probability Models: Logit, Probit, and Other Generalized Linear Models. Thousand Oaks, CA: Sage Publications, Inc.
Powers, D. and Xie, Yu. Statistical Methods for Categorical Data Analysis. Bingley, UK: Emerald Group Publishing Limited.