成績とスマホ利用時間のみをアピールする恣意性

香川のネット・ゲーム条例で、1時間以上のスマホ利用で成績が下がるという件について(参考))。もともとの資料は平成30年度『香川県学習状況調査』である。

www.kagawa-edu.jp

この報告書では成績と関連についてかなり重点的に書かれてある。
もともと学習調査なので当たり前といえば当たり前である。この報告書で着目すべきはスマホ利用以外の多くの項目も成績との関連がみられることである。

まずはスマホ利用から見ていこう。

スマホ使用時間と成績

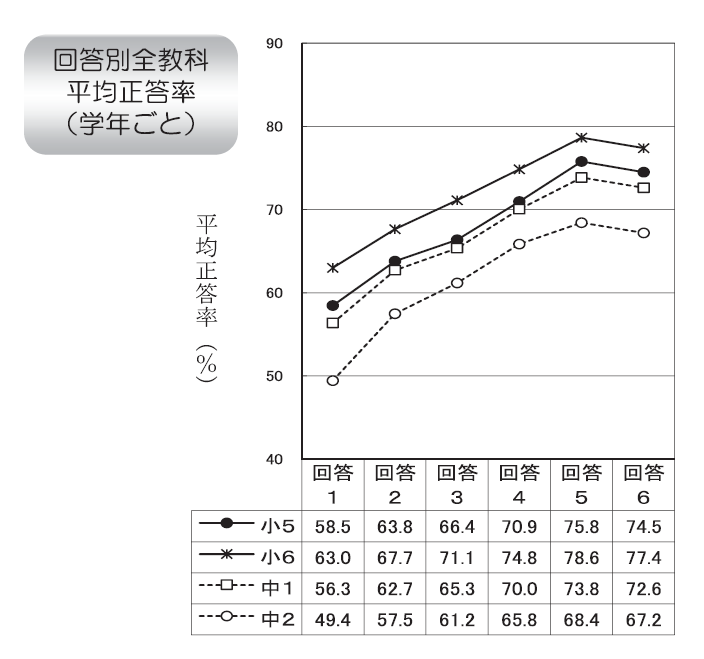
回答1: 4時間以上
回答2: 3-4時間
回答3: 2-3時間
回答4: 1-2時間
回答5: 1時間未満
回答6: ゼロ

報告書には、平均値と人数(学力テスト参加者のもので代用)と相関係数が掲載されているので、仮想データは一応作成できる。

1時間未満、1時間以上の2カテゴリに分けて、分散分析をすると、確かに統計学的に有意な差がある。
後段の付録のところで仮想データを作成して計算したものを掲載している。

スマホ利用がゼロのグループの成績がやや落ちているという指摘もしていただいたので、最も成績の良い1時間未満グループと、ゼロのグループで比較してみたところ、P=.111であり、作成した仮想データでは明確な差が得られなかった。

ただ、統計学的には、1時間以上／未満という分け方をすると、学力テストの結果に差は出る。スマホ使用時間と成績に相関関係はあるのは間違いないだろう。ただ、相関関係は因果関係とは異なっていて、スマホ利用をするとテストの点が落ちることを意味していないことに注意する必要がある。

グラフの描き方

グラフの描き方の恣意性も指摘されている。
報告書のグラフの縦軸は40点からしか表示されていないので、差が大きく誇張されている。

恣意的な加工をしないため、Excelのデフォルトで出てくる形のグラフをそのまま採用した。デフォルトでは縦軸の範囲は0-90であった。

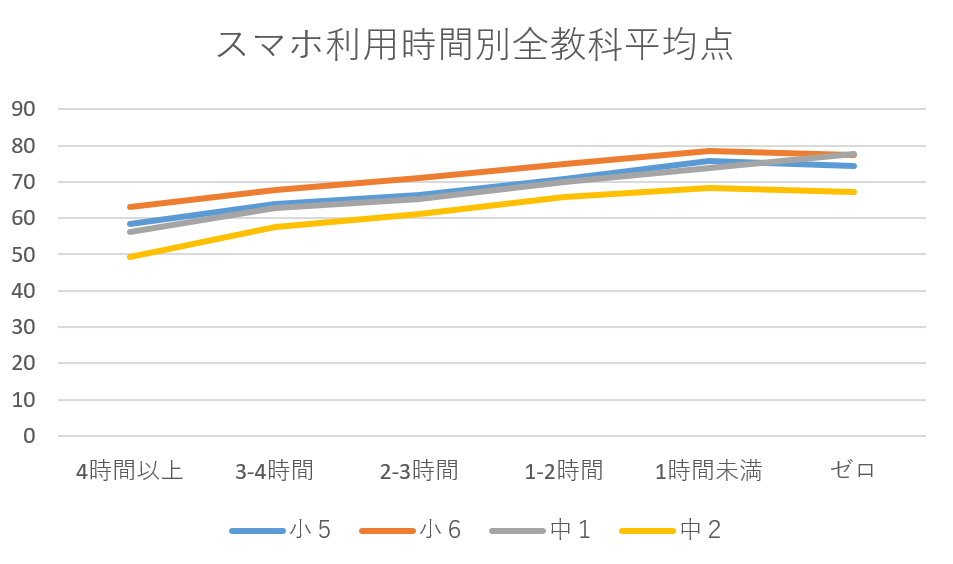
多少印象は異なってくるかもしれない。

だいたいの調査項目がスマホ利用と同様の結果になっている

ネット・ゲーム条例を念頭にこの報告書と興味深いのがこの部分である。
スマホ利用と成績のグラフだけを取り出すと、「あー、確かに成績との関連があるんだな」「スマホを使用すると成績が落ちるんだな」と思うのも無理はないが、実は他の調査項目のほとんどが、スマホ利用と同じような分布のグラフになっているのだ。早速確認していこう。

1. 朝食を毎日食べていますか

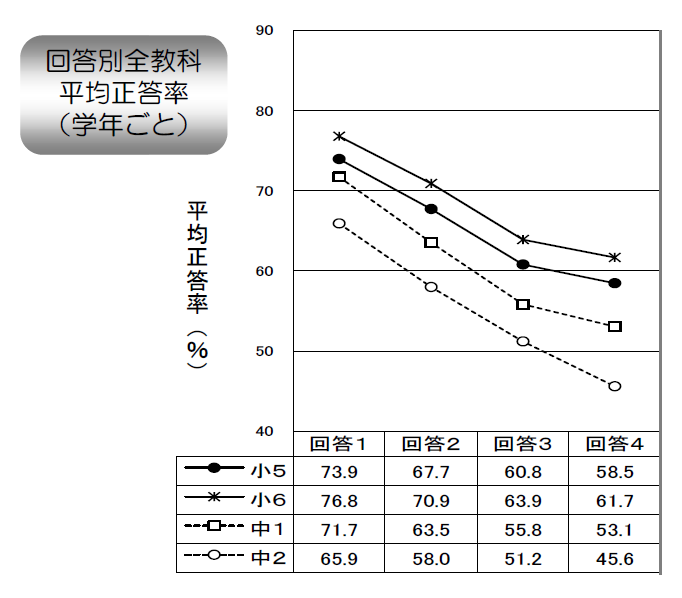
１毎日食べている
２食べる日の方が多い
３食べない日の方が多い
４まったく食べていない
５その他

2. 家の人(兄弟姉妹を含みません。)と学校でのできごとについて話をしていますか

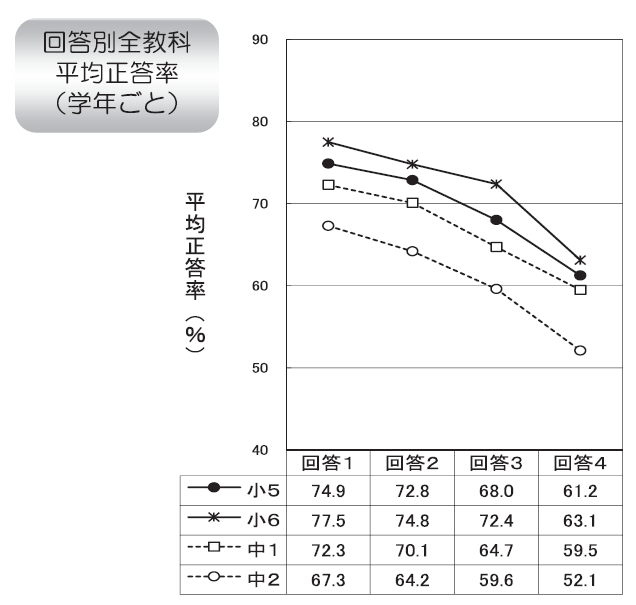
1. している
2. どちらかといえばしている
3. あまりしていない
4. していない

4. ものごとを最後までやりとげて、うれしかったことがありますか

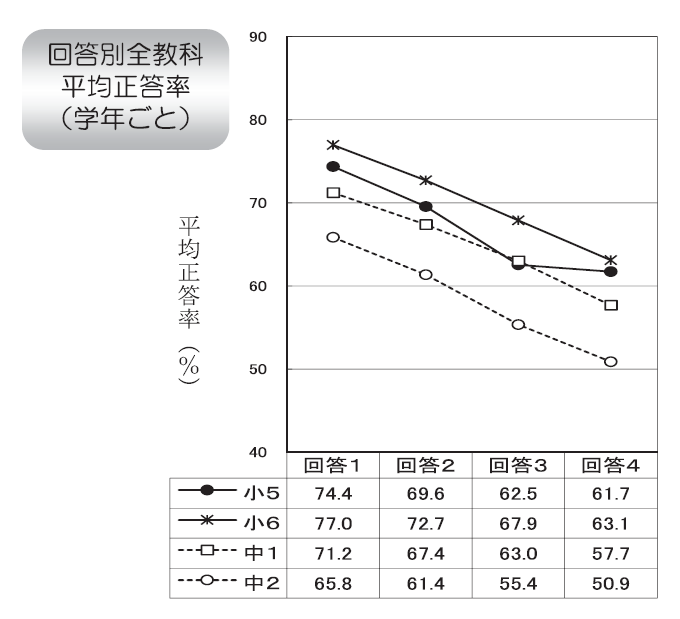
1. ある
2. どらかといえばある
3. どらかといえばない
4. ない

5. むずかしいことでも、失敗をおそれないで挑戦していますか

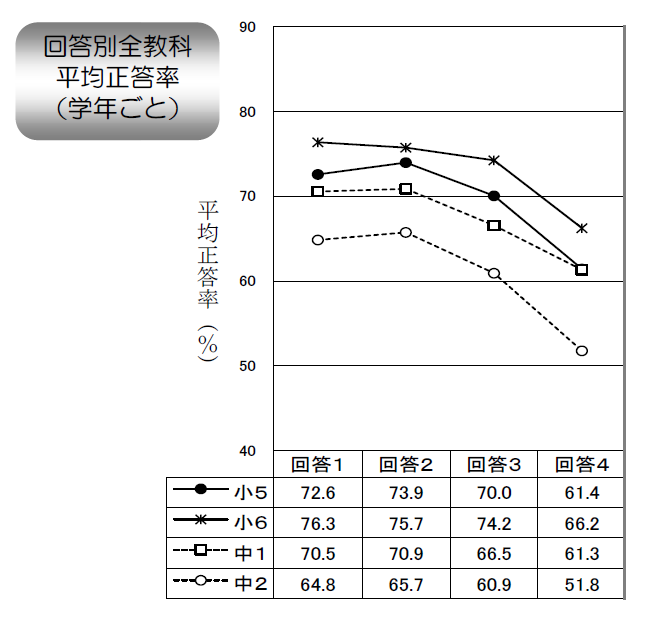
1. している
2. どちらかといえばしている
3. あまりしていない
4. していない

6. 自分には、よいところがあると思いますか

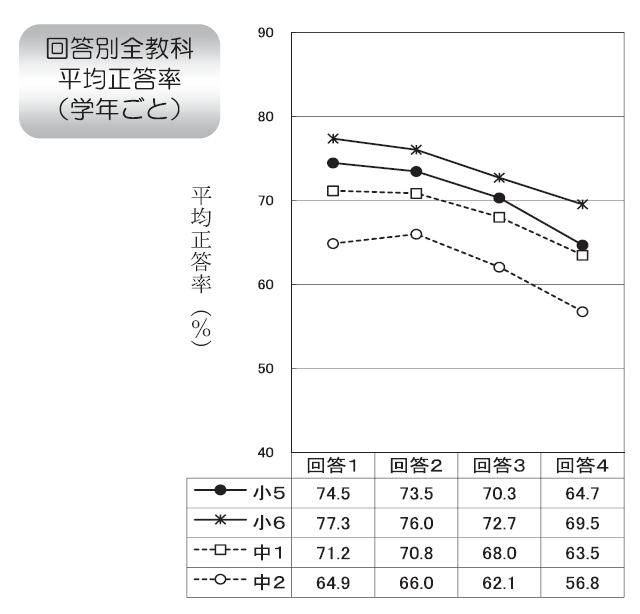
1. 思う
2. どちらかといえば思う
3. あまり思わない
4. まったく思わない

8. 学校のきまりを守っていますか

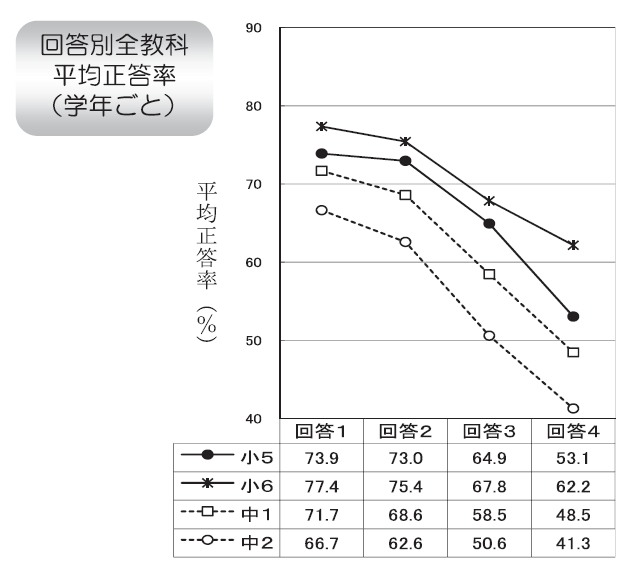
1. 守っている
2. どちらかといえば守っている
3. あまり守っていない
4. 守っていない

9. 係や委員の仕事など、自分の役割をきちんと果たしていますか

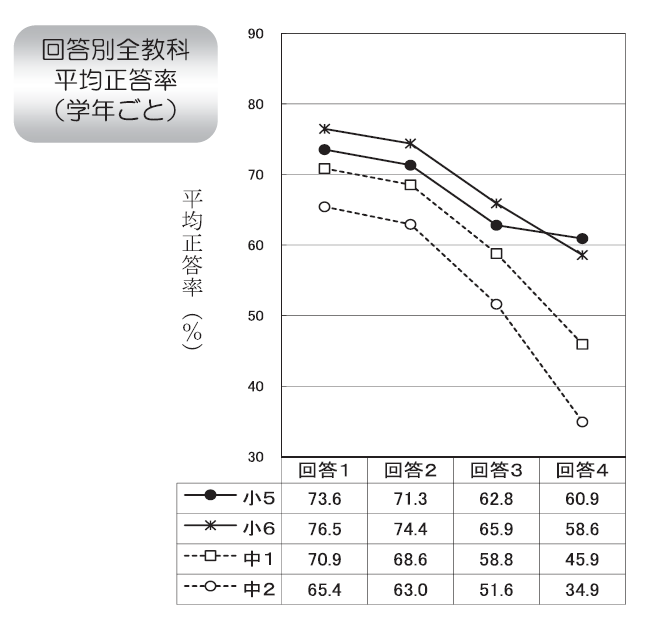
1. している
2. どちらかといえばしている
3. あまりしていない
4. まったくしていない

10. 人が困っているときは、進んで助けていますか

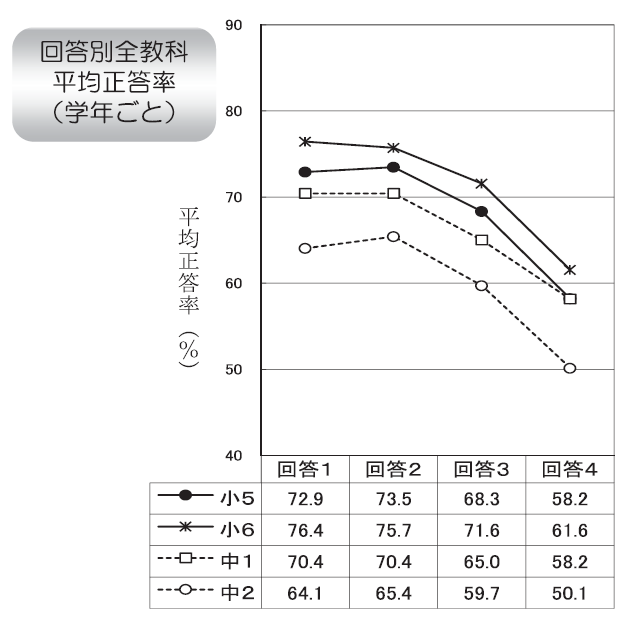
1. している
2. どちらかといえばしている
3. あまりしていない
4. まったくしていない

11. 近所の人に会った時は、挨拶をしていますか

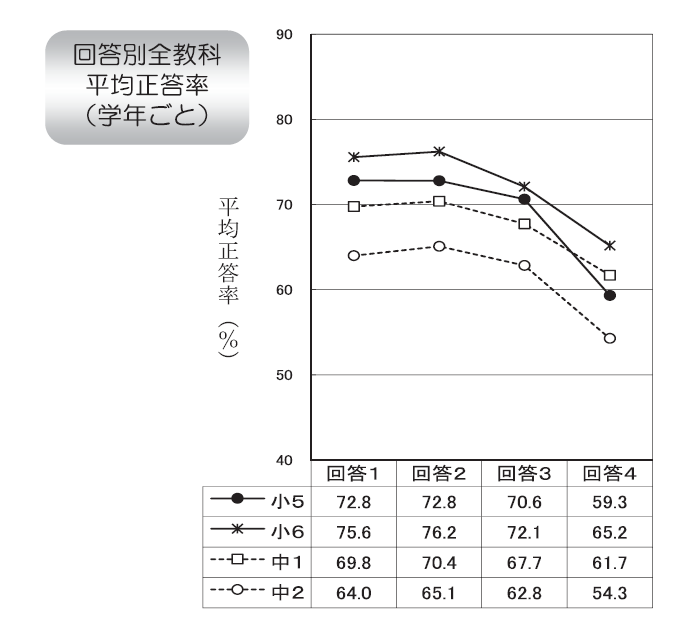
1. している
2. どちらかといえばしている
3. あまりしていない
4. まったくしていない

12. 人の気持ちがわかる人間になりたいと思いますか

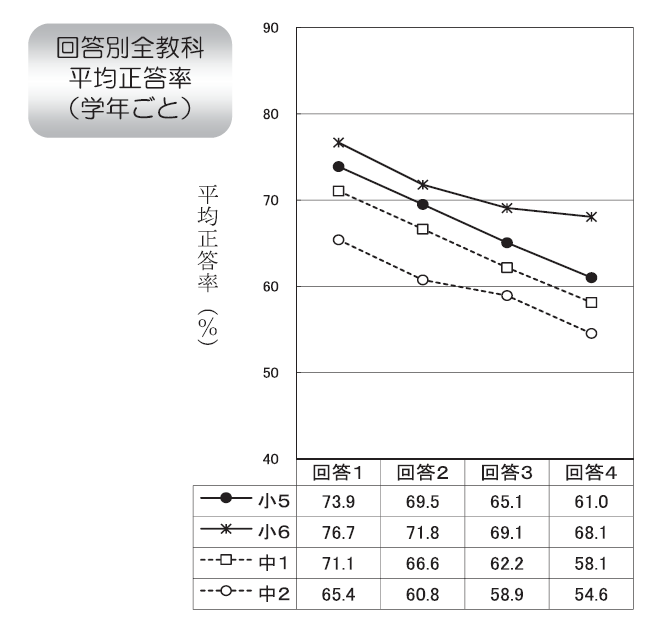
1. 思う
2. どちらかといえば思う
3. あまり思わない
4. まったく思わない

13. いじめは、どんな理由があってもいけないことだと思いますか

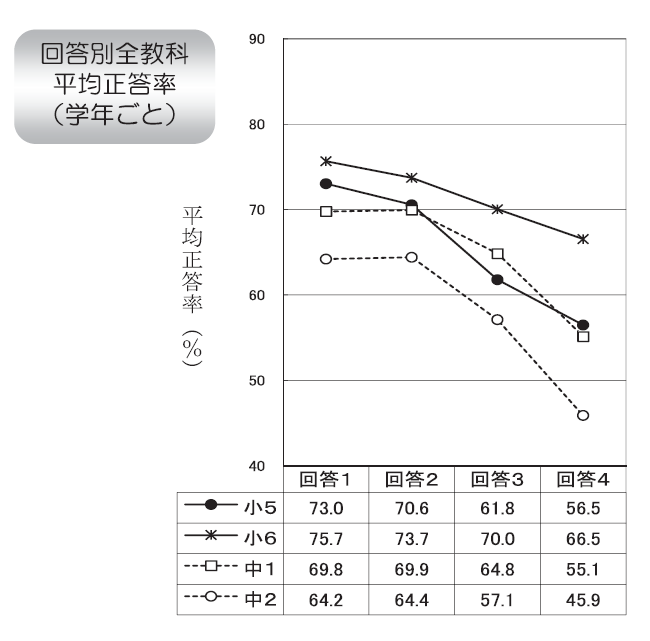
1. 思う
2. どちらかといえば思う
3. あまり思わない
4. まったく思わない

14. 人の役に立つ人間になりたいと思いますか

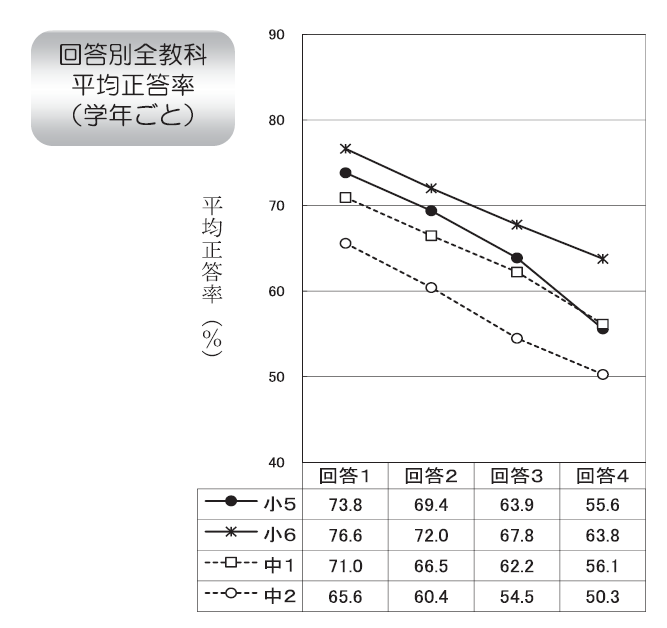
1. 思う
2. どちらかといえば思う
3. あまり思わない
4. まったく思わない

15. 新聞やテレビのニュースなどに関心がありますか

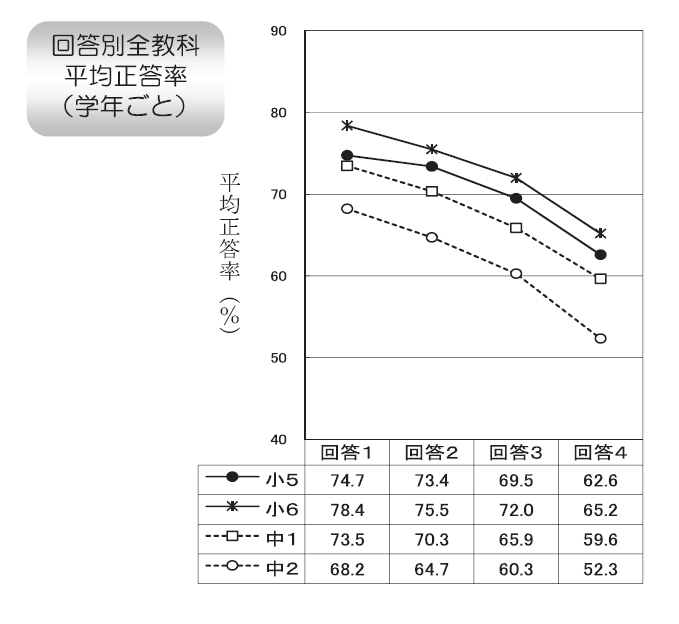
1. ある
2. どらかといえばある
3. どらかといえばない
4. ない

21. 友達と話し合うときに、友達の意見を最後まで聞くことができますか

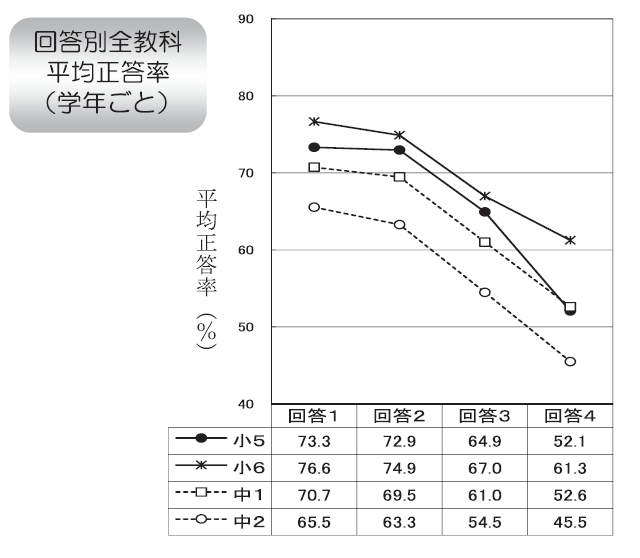
1. している
2. どちらかといえばしている
3. あまりしていない
4. していない

22. 授業では、ノートをていねいに書いていますか

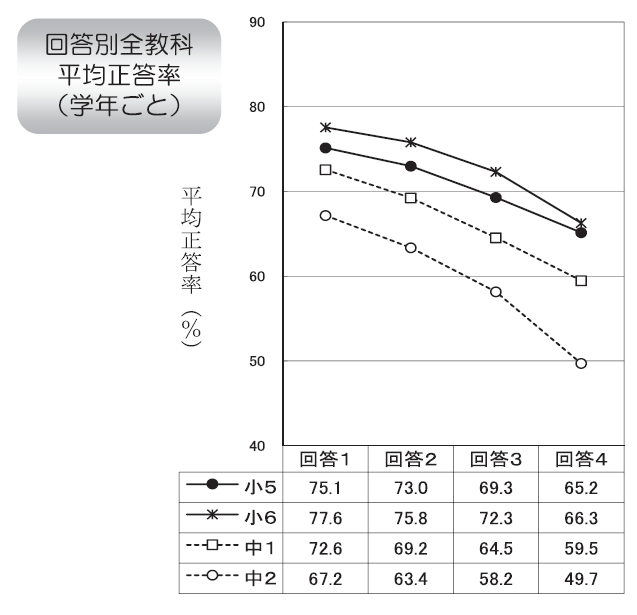
1. している
2. どちらかといえばしている
3. あまりしていない
4. していない

23. 勉強は好きですか

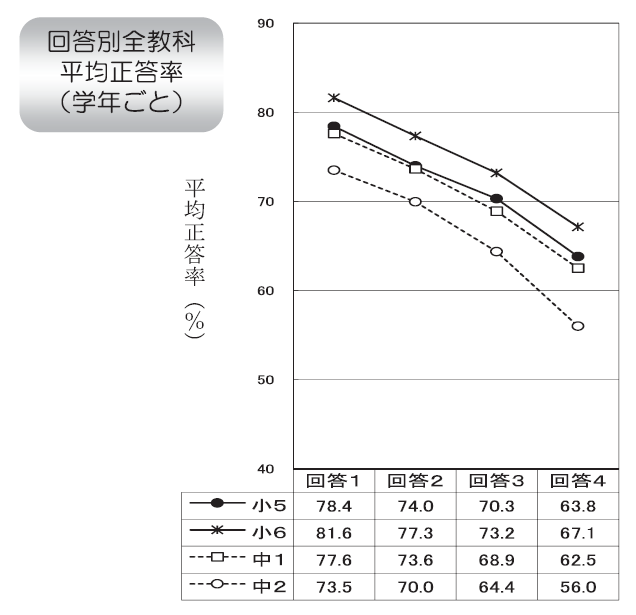1. 好き 2. どちらかといえば好き 3. どちらかといえばきらい 4. きらい

26. 授業がどの程度わかりますか

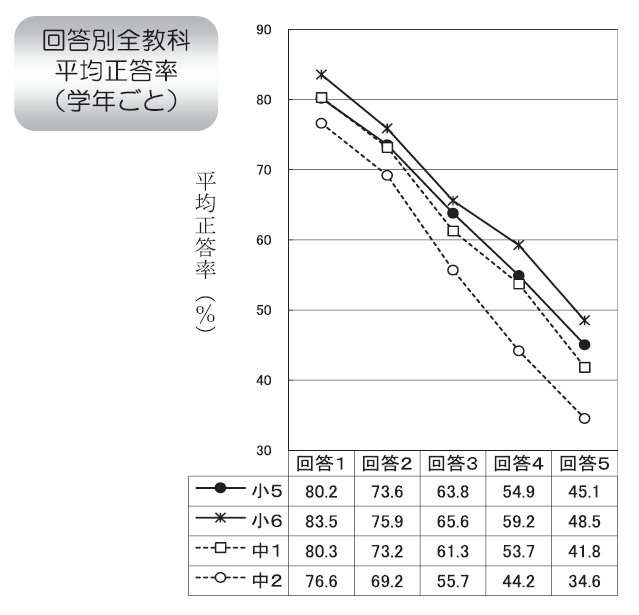
1. よく分かる
2. だたい分かる
3. 分かることと分からないことが半分ずつある
4. 分からないことが多い
5. ほとんど分からない

最も相関係数が高い質問項目で、中学校では0.5くらいである。 勉強関係はだいたい同じ傾向があるので、残りの項目は割愛する。

スマホ利用と同じような傾向を示す項目

1. 朝食を毎日食べていますか
2. 家の人(兄弟姉妹を含みません。)と学校でのできごとについて話をしていますか
3. ものごとを最後までやりとげて、うれしかったことがありますか
4. むずかしいことでも、失敗をおそれないで挑戦していますか6. 自分には、よいところがあると思いますか
5. 学校のきまりを守っていますか
6. 係や委員の仕事など、自分の役割をきちんと果たしていますか
7. 人が困っているときは、進んで助けていますか
8. 近所の人に会った時は、挨拶をしていますか
9. 人の気持ちがわかる人間になりたいと思いますか
10. いじめは、どんな理由があってもいけないことだと思いますか
11. 人の役に立つ人間になりたいと思いますか
12. 新聞やテレビのニュースなどに関心がありますか
13. 友達と話し合うときに、友達の意見を最後まで聞くことができますか
14. 授業では、ノートをていねいに書いていますか
15. 勉強は好きですか
16. 授業がどの程度わかりますか

考察

以上の項目から2つの点が指摘できるだろう。

1. 同じような関連が項目の中でわざわざスマホ利用を取り出してきたのか恣意的。
2. 同じような関連を示す項目がこれだけある場合、成績低下の原因をスマホに還元するのは現実的ではない。

1. スマホ利用だけを取り出すのは恣意的

近所の人にあいさつをするという項目でも同じような分布になっている。近所の人にあいさつをする条例でもよかったはず。
つまり、この報告書のグラフを見て、スマホを制限したら成績が上がると考えるのは、近所の人にあいさつをすると成績が上がると考えるのと同じなのである。
挨拶に置き換えると、香川県条例の論拠のデタラメさが良くわかるはずである。

2. 成績低下の原因をスマホに還元できない

スマホ利用と成績の2変数だけだと統計学的に有意な相関関係がみられる。しかし、これだけ様々な項目が関連しているならば、他の項目をコントール、つまり多変量解析すると、スマホ利用と成績の関連がみられない可能性は非常に高い。

成績低下とスマホ利用が因果関係にあるのであれば、多変量解析で結果を示す必要がある。
それをせずに、スマホ利用と成績の関連だけにクローズアップするのは、本当の原因・因果関係を隠蔽したいと言っているのと同じである。

付録: 仮想データによるシミュレーション

Rで仮想データを作成した。
3つ以上のカテゴリに分けられたデータの仮想データの再現度はあまり高くないため、参考程度に捉えてもらいたい。
ごとのテストスコアの標準偏差は16.6、スマホ使用時間の表示偏差は0.4と仮定し、各カテゴリ内の相関係数は+0.5と仮定している。また分布は正規分布を仮定している。 つまり、この4つの仮定は仮定にすぎず、相関係数を一致させるために調整したものであり、この仮定か元データとは異なっている。

元データを見ていないので予想にすぎないが、スマホ使用ゼロのグループは標準偏差が他のカテゴリより大きいのではないかと思われる。スマホを持たないというグループは他のグループに比べて少数派であるために、その中でも多様性があると推測できるからだ。仮想データは4つの仮定を立てて作成されているので、元データで分析すると、有意でなかったものが有意関連となる可能性もある。ただ、1時間で２グループに分けて平均値の比較をする場合、おそらくどのような仮定をおいても有意な差はあるだろう。

4時間以上

library(splus2R)
set.seed(1234) # 乱数シードの固定
N_5 <-893  # サンプルサイズの指定
Sigma_5 = matrix(c(1,0.5,0.5,1), byrow=TRUE, ncol=2) # c()の中に相関係数を入れる。
mu_5 <- c(49.4, 5.5) # 平均値
d5 <- data.frame(rmvnorm(n=N_5, mean=mu_5, cov=Sigma_5, sd=c(16.6,0.4))) # 乱数の作成
colnames(d5) <- c("Kokugo","Phone_Time") # 列名を挿入
d5$Kokugo <- round(d5$Kokugo) # まるめ(点数を四捨五入で整数値に)
d5$Phone_Time <- round(d5$Phone_Time, digits = 1) # まるめ(スマホ時間を少数第一位に)

3-4時間

library(splus2R)
set.seed(1234) # 乱数シードの固定
N_4 <-876  # サンプルサイズの指定
Sigma_4 = matrix(c(1,0.5,0.5,1), byrow=TRUE, ncol=2) # c()の中に相関係数を入れる。
mu_4 <- c(47.5, 3.5) # 平均値
d4 <- data.frame(rmvnorm(n=N_4, mean=mu_4, cov=Sigma_4, sd=c(16.6,0.4))) # 乱数の作成
colnames(d4) <- c("Kokugo","Phone_Time") # 列名を挿入
d4$Kokugo <- round(d4$Kokugo) # まるめ(点数を四捨五入で整数値に)
d4$Phone_Time <- round(d4$Phone_Time, digits = 1) # まるめ(スマホ時間を少数第一位に)

2-3時間

library(splus2R)
set.seed(1234) # 乱数シードの固定
N_3 <-1597  # サンプルサイズの指定
Sigma_3 = matrix(c(1,0.5,0.5,1), byrow=TRUE, ncol=2) # c()の中に相関係数を入れる。
mu_3 <- c(47.5, 2.5) # 平均値
d3 <- data.frame(rmvnorm(n=N_3, mean=mu_3, cov=Sigma_3, sd=c(16.6,0.4))) # 乱数の作成
colnames(d3) <- c("Kokugo","Phone_Time") # 列名を挿入
d3$Kokugo <- round(d3$Kokugo) # まるめ(点数を四捨五入で整数値に)
d3$Phone_Time <- round(d3$Phone_Time, digits = 1) # まるめ(スマホ時間を少数第一位に)

1-2時間

library(splus2R)
set.seed(1234) # 乱数シードの固定
N_2 <- 1974  # サンプルサイズの指定
Sigma_2 = matrix(c(1,0.5,0.5,1), byrow=TRUE, ncol=2) # c()の中に相関係数を入れる。
mu_2 <- c(65.8, 1.5) # 平均値
d2 <- data.frame(rmvnorm(n=N_2, mean=mu_2, cov=Sigma_2, sd=c(16.6,0.4))) # 乱数の作成
colnames(d2) <- c("Kokugo","Phone_Time") # 列名を挿入
d2$Kokugo <- round(d2$Kokugo) # まるめ(点数を四捨五入で整数値に)
d2$Phone_Time <- round(d2$Phone_Time, digits = 1) # まるめ(スマホ時間を少数第一位に)

1時間未満

library(splus2R)
set.seed(1234) # 乱数シードの固定
N_1 <-1769  # サンプルサイズの指定
Sigma_1 = matrix(c(1,0.5,0.5,1), byrow=TRUE, ncol=2) # c()の中に相関係数を入れる。
mu_1 <- c(68.4, 0.5) # 平均値
d1 <- data.frame(rmvnorm(n=N_1, mean=mu_1, cov=Sigma_1, sd=c(16.6,0.4))) # 乱数の作成
colnames(d1) <- c("Kokugo","Phone_Time") # 列名を挿入
d1$Kokugo <- round(d1$Kokugo) # まるめ(四捨五入で整数値に)
d1$Phone_Time <- round(d1$Phone_Time, digits = 1) # まるめ(スマホ時間を少数第一位に)

ゼロ

library(splus2R)
set.seed(1234) # 乱数シードの固定
N_0 <-1048   # サンプルサイズの指定
Sigma_0 = matrix(c(1,0.5,0.5,1), byrow=TRUE, ncol=2) # c()の中に相関係数を入れる。
mu_0 <- c(67.2, 0) # 平均値
d0 <- data.frame(rmvnorm(n=N_0, mean=mu_0, cov=Sigma_0, sd=c(16.6,0.4))) # 乱数の作成
colnames(d0) <- c("Kokugo","Phone_Time") # 列名を挿入
d0$Kokugo <- round(d0$Kokugo) # まるめ(四捨五入で整数値に)
d0$Phone_Time <- round(replace(d0$Phone_Time, 1:1048, 0)) # スマホ時間に0を代入

データ結合

data12 <-merge(d1, d2 ,all=T, sort=F)
data13 <-merge(data12, d3 ,all=T, sort=F)
data14 <-merge(data13, d4 ,all=T, sort=F)
data15 <-merge(data14, d5 ,all=T, sort=F)
data <-merge(data15, d0 ,all=T, sort=F)
plot(data)

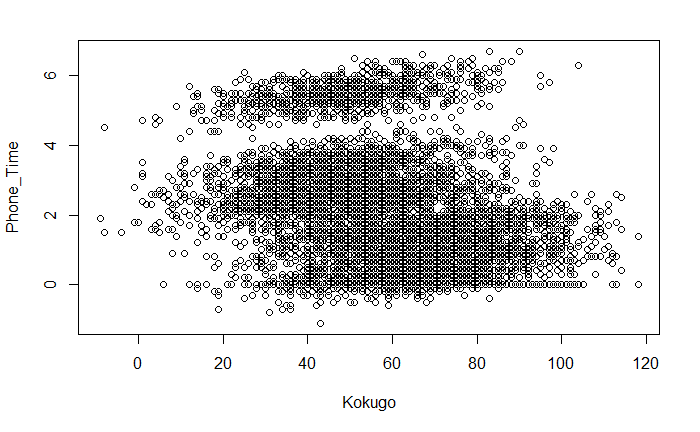
相関係数

cor(data$Kokugo, data$Phone_Time)

[1] -0.3070171

1時間で切った場合

library(dplyr)
data$Phone_1<-data$Phone
data <- mutate(data, Phone_1 = if_else(condition = Phone_Time > 1, true = "1", false = "0"))
table(data$Phone_1)

res01 <- aov(Kokugo ~ Phone_1, data =data) # 分散分析
summary(res01) # 結果表示
with(data, tapply(Kokugo, Phone_1, mean, na.rm=TRUE)) #　平均値の計算

              Df  Sum Sq Mean Sq F value Pr(>F)    
Phone_1        1  200670  200670   621.2 <2e-16 ***
Residuals   8425 2721366     323                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
       0        1 
65.02478 55.05297