こちらの論文で挙げられている方法を検討した。
- Weiss, B.A. and Dardick, W. (2016) ‘An Entropy-Based Measure for Assessing Fuzziness in Logistic Regression’, Educational and Psychological Measurement, 76(6), pp. 986–1004. Available at: https://doi.org/10.1177/0013164415623820.
二項ロジスティック回帰分析の推定
例題として使うので、適当に二項ロジスティック回帰分析の推定をしておく。
library(AER) data(CPS1985) head(CPS1985)
wage education experience age ethnicity region gender occupation sector union married 1 5.10 8 21 35 hispanic other female worker manufacturing no yes 1100 4.95 9 42 57 cauc other female worker manufacturing no yes 2 6.67 12 1 19 cauc other male worker manufacturing no no 3 4.00 12 4 22 cauc other male worker other no no 4 7.50 12 17 35 cauc other male worker other no yes 5 13.07 13 9 28 cauc other male worker other yes no
# 二項ロジスティック回帰分析
fit <- glm(union ~ age + gender + wage + occupation,
data = CPS1985, family = binomial(link = "logit"))
summary(fit)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.68778 0.46643 -5.762 8.29e-09 ***
age 0.02968 0.01028 2.886 0.003905 **
genderfemale -0.61376 0.28655 -2.142 0.032204 *
wage 0.08753 0.02518 3.477 0.000508 ***
occupationtechnical -0.55867 0.33890 -1.648 0.099258 .
occupationservices -0.09986 0.35508 -0.281 0.778535
occupationoffice -1.07916 0.44743 -2.412 0.015870 *
occupationsales -2.76139 1.04795 -2.635 0.008412 **
occupationmanagement -2.54377 0.67700 -3.757 0.000172 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 503.08 on 533 degrees of freedom
Residual deviance: 437.81 on 525 degrees of freedom
AIC: 455.81
Number of Fisher Scoring iterations: 6
逸脱度 deviance (-2LL)
ロジスティック回帰分析では、逸脱度 (-2LL) は、適合モデルを飽和モデルと比較することで、モデルの適合の欠如を表す数学量である (Cohen, Cohen, West, & Aiken, 2003)。そのため、観察された値が期待値とどれくらい違うかを表します。尤度比は、あるモデルの最大尤度と別のモデルの最大尤度の比であり、逸脱度は尤度比の対数に(-2)を乗じて計算される。デビアンス値がゼロの場合は完全な適合を表し、値が大きい場合は適合が悪いことを示す。逸脱度は、必ずしもカイ二乗分布に従うとは限らないので、それ自体で解釈するよりも、モデル比較に有用である (O'Connell & Amico, 2010; Peng, So, Stage, & St. John, 2002)。
尤度比χ2検定
尤度比カイ2乗検定 (LR χ2) は、より小さなモデル（多くの場合、ベースラインまたは切片のみのモデル）をより大きなモデルと比較するために逸脱度を用いる。対数尤度の変化は、2つのモデル間の-2LL値の差を取ることによって計算さ れる。-2LLの差はカイ2乗分布に従うので、その値はカイ2乗臨界値と比較できる。統計的に有意な結果は、より多くの予測変数を持つモデルが、より少ない予測変数を持つモデルよりも統計的に有意によくデータに適合することを示す。この検定の利点は、理論モデルがベースライン・モデルよりもよく適合するかどうかを決定するのに有用であり、入れ子モデルを比較する統計的検定として使用できることである。LR χ2 は、データが疎であるとき（しばしば連続的に測定される予測変数が使用されるときの結果）、または標本サイズが大きいときのデータ-モデル適合の限定された測定である。
Hosmer-Lemeshowカイ二乗検定
Hosmer-Lemeshowカイ二乗検定も適合度検定の一種で、データが疎な場合に有用である。この統計量は、予測された確率をパーセンタイル・ランクに基づく10個のグループ（十分位）に分割し、Pearson χ2を計算して、観察された度数と期待される度数を比較する。非統計的に有意な結果は、データとモデルの適合が良好であることを示す。この統計量は、保守的な検定（すなわち、低い第一種過誤率; Peng et al., 2002）とみなされ、連続予測変数が使用される場合に有用である。この尺度は、検出力の欠如を批判され、したがって、n > 400の場合のみ推奨される (Hosmer & Lemeshow, 2000)。対照的に、カイ2乗検定は、一般に標本サイズに非常に敏感で、したがって、大きなnでは、しばしば統計的に有意な結果（データ・モデルの適合が悪いことを示す）を出す。したがって、この検定の理想的な検出力のために必要な標本サイズのコンセンサスはありません。さらに、この尺度は、十進分類を作成するために使用されるカット・ポイントに敏感であり、したがって、数値HL χ2値は、ソフトウェア・プログラムによって異なる可能性がある(Hosmer, Hosmer, Le Cessie, & Lemeshow, 1997; Peng et al., 2002)。
Hosmer-Lemeshowカイ二乗検定の実行
すべてnumeric型にしないと走らないので、変数をいじる必要がある。
library(dplyr)
CPS1985$gender.num <- CPS1985$gender
CPS1985 <- CPS1985 %>%
mutate(gender.num = case_when(
gender.num == "male" ~ 1,
gender.num == "female" ~ 2))
CPS1985$occupation.num <- CPS1985$occupation
CPS1985 <- CPS1985 %>%
mutate(occupation.num = case_when(
occupation.num == "worker" ~ 1,
occupation.num == "technical" ~ 2,
occupation.num == "services" ~ 3,
occupation.num == "office" ~ 4,
occupation.num == "sales" ~ 5,
occupation.num == "management" ~ 6
))
CPS1985$union.num <- CPS1985$union
CPS1985 <- CPS1985 %>%
mutate(union.num = case_when(
union.num == "yes" ~ 1,
union.num == "no" ~ 0))
### 従属変数のみのデータをpredprobに格納
predprob <- data.frame(age = CPS1985$age, gender = CPS1985$gender,
wage = CPS1985$wage, occupation = CPS1985$occupation)
### numeric型の変数を用いたモデルを作成
fit2 <- glm(union.num ~ age + gender.num + wage + occupation.num,
data = CPS1985, family = binomial(link = "logit"))
### Hosmer-Lemeshow検定を実行
hl_gof <- hoslem.test(CPS1985$union.num, fitted(fit2), g = 10)
hl_gof
5%水準以下の小さなP値は、モデルが不完全であることを示唆する。
Hosmer and Lemeshow goodness of fit (GOF) test data: CPS1985$union.num, fitted(fit2) X-squared = 3.5246, df = 8, p-value = 0.8973
擬似R二乗（分散説明）尺度
ロジスティック回帰では、モデルがデータにどれだけよく適合するかの効果量測定として、いくつかの擬似分散説明尺度が使用されることがある（たとえば、McFaddenのR2, Cox & Snell, 1989; Nagelkerke, 1991）。これらは、通常の最小2乗（OLS）回帰における多重R2と同様に解釈されることを意図しているが、カテゴリー的な結果の分散が連続的な結果の分散と異なるので、擬似R2指標とみなされる(Lomax & Hahs-Vaughn, 2012)。 これらの指標は、0から1の範囲（1はより良いデータ・モデル適合を示す）を意味するが、Cox and Snell (1989) の指標が1.0に等しくなることは数学的に不可能であり、どの擬似分散説明指標についても推奨されるカットオフ値は現在のところ存在しない。これらのうち、McFaddenのR2指数は、その解釈が重回帰のR2に最も似ているため、最も直感的に理解できますが、多くの市販統計ソフトでは利用できないため、手作業で計算しなければならず、一部の応用研究者にとっては望ましくない尺度となっています (O'Connell & Amico, 2010; Peng et al., 2002)。さらに、どの擬似R2値を報告するのが望ましいかについては、研究者の間でも意見が分かれている(O'Connell & Amico, 2010)。
RではDescToolsパッケージを用いて容易に計算ができる。
library(DescTools) PseudoR2(fit, which = "all")
McFadden McFaddenAdj CoxSnell Nagelkerke AldrichNelson VeallZimmermann Efron McKelveyZavoina Tjur
0.12973875 0.09395945 0.11505302 0.18855166 0.10891512 0.22452336 0.12640844 0.28229487 0.12434253
AIC BIC logLik logLik0 G2
455.81462887 494.33819142 -218.90731444 -251.54206888 65.26950888
正確性 accuracy / 正しく分類されたケースの割合
多くの研究者は、観察されたグループ・メンバーシップと予測されたグループ・メンバーシップのクロス集計を含む分類表に依存している。バイナリ・ロジスティック回帰では、予測確率が0.5以上のケースは、通常1つのグループに分類され、一方、予測確率が0.5未満のケースは、2番目のグループで予測されたグループ・メンバーシップになる（ただし、必要であれば、研究者は0.5以外のカット・ポイントを選択できる）。クロス集計表に基づいて、正しく分類されたケースのパーセンテージが計算され、データ・モデルの適合の尺度として使用できる。バイナリ・ロジスティック回帰のケースでは、分類率の値は、50% から100%の正しい分類の範囲であり、より大きな値は、よりよいデータ・モデルの適合を示す。
正しい分類のパーセンテージは、観察された頻度の小さいグループの誤分類率が大きいこと（特に、あるグループの標本サイズが小さいとき）、1つまたは複数のグループの潜在的な悪い分類率、したがって、分類率内のこれらのグループの過小表現、および基本率または偶然の分類が組み込まれていないこと（Lomax & Hahs-Vaughn, 2012; O'Connell & Amico, 2010）により、データ・モデルの適合の効果的な尺度でないと批判されることが多い。さらに、モデルはデータによく適合していると考えられるが、分類率が低いという状況も起こり得る。
正確性 accuracy の計算
回帰分析の推定結果を計算し、それを2値データに変換する。これが推定値である。
一方でもともとの従属変数がある。従属変数に比べて、推定モデルによって推定された結果は何%あっているのか、という計算をする。
caretパッケージのconfusionMatrix関数を使う。計算はnumeric型でしかできないため、先ほどの二項ロジスティック回帰分析の従属変数であった、unionをunion.numという変数にコピーして、これをnumeric型に変換しておく。
比較のための変数を作成する
## dplyrでCPS1985$unionのyesを1に、noを0に変換する
library(dplyr)
CPS1985$union.num <- CPS1985$union
CPS1985 <- CPS1985 %>%
mutate(union.num = case_when(
union.num == "yes" ~ 1,
union.num == "no" ~ 0))
library(caret)
### type = "response" 各観測に対して予測確率を与える
pred_probs <- predict(fit, CPS1985, type = "response")
### 予測値を2値変数に変換する
pred_diagn <- ifelse(pred_probs > 0.5, 1, 0)
### 混同行列と精度
caret::confusionMatrix(data = as.factor(pred_diagn),
reference = as.factor(CPS1985$union.num))
結果
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 431 89
1 7 7
Accuracy : 0.8202
95% CI : (0.785, 0.8519)
No Information Rate : 0.8202
P-Value [Acc > NIR] : 0.5272
Kappa : 0.0854
Mcnemar's Test P-Value : <2e-16
Sensitivity : 0.98402
Specificity : 0.07292
Pos Pred Value : 0.82885
Neg Pred Value : 0.50000
Prevalence : 0.82022
Detection Rate : 0.80712
Detection Prevalence : 0.97378
Balanced Accuracy : 0.52847
'Positive' Class : 0
この二項ロジスティック回帰モデルの正確性82.02%であった。
ROC曲線 Receiver Operating Characteristic Curves
モデルがデータに合っているかどうかを判断するために使用できる視覚的な検査方法もいくつかある。ROC曲線は、感度（真陽性、すなわち、イベントとして正しく分類されたケースのパーセンテージ）と1-特異度（偽陽性、すなわち、イベントとして誤って分類されたケースのパーセンテージ）を比較する。したがって、ROC曲線は、ある割合の症例を正しく分類するために、誤分類される必要のある症例の割合を示している。ROC 曲線は、0.50以外のカット・ポイントを識別するためのバイナリ・ロジスティック回帰でも有用である。
AUC; Area Under the Receiver Operating Characteristic Curve
ROC曲線の主な限界は、ROC曲線は視覚的な検査しかできないため、データとモデルの適合に関する解釈が主観的であることである。しかし研究者は、ROC曲線を用いて曲線下面積（AUC）を計算することができる。AUCは、データ-モデル適合の尺度として使用できる単一の数値を報告することで、曲線を定量化する。概念的には、AUCは一致確率であり、無作為に選んだ陽性症例が無作為に選んだ別の陰性症例より高いスコアを出す確率である。曲線が左上隅に近いほど、AUCは大きい。二項ロジスティック回帰では、AUCは0.5 から 1.0の範囲で、値が高いほどデータ・モデルの適合がよいことを示す。AUC は、Wilcoxonの順位検定と同じ結果を生成する (Streiner & Cairney, 2007)。経験則として、AUC値が0.5～0.7は低いとみなされ、0.7～0.9は中程度、0.9より大きい値は高いとみなされる(Streiner & Cairney, 2007)。t検定は、AUCが0.5から統計的に有意に異なるかどうかを決定するために計算することができる。統計的に有意なAUC値は、モデルが偶然よりもよく適合していることを示す。研究者によっては、AUC推定値の周りの95%信頼区間を報告する。
データとモデルの適合の尺度としてROC曲線とAUCを用いることには多くの問題がある。第一に、感度と特異度の値はカットポイントがどこにあるかによって決まるため、AUCは無限に計算できる。さらに、ROC曲線は分散を考慮しておらず、ROC曲線が交差する可能性があるため、直接比較できないことから、モデル比較にROC曲線を使用することに注意を促す研究者もいる（Fawcett, 2005; Streiner & Cairney, 2007）。
注：AUCは要するに順序に関する計算であり、分散が考慮されないということ。
ROC曲線下面積(AUC)
正確性加えて、ROC曲線下面積（AUC）は、モデルの予測可能性を評価するために用いることができる。AUCが高いほど良いモデルである。
AUC曲線の計算を行う。
## 真の値と予測確率のデータフレームを作成する
eval_df <- data.frame(CPS1985$union.num, pred_probs)
colnames(eval_df) <- c("truth", "pred_probs")
eval_df$truth <- as.factor(eval_df$truth)
### AUCを計算する
library(yardstick)
roc_auc(eval_df, truth, pred_probs, event_level = "second")
結果
.metric .estimator .estimate <chr> <chr> <dbl> 1 roc_auc binary 0.755
AUCスコアは75.50%であった。
次に、ggplot2でROC曲線をプロットする。
library(yardstick)
library(ggplot2)
library(dplyr)
## plot ROC
roc_curve(eval_df, truth, pred_probs, event_level = "second") %>%
ggplot(aes(x = 1 - specificity, y = sensitivity)) +
geom_path() +
geom_abline(lty = 3, col = "red") +
coord_equal() +
theme_bw()
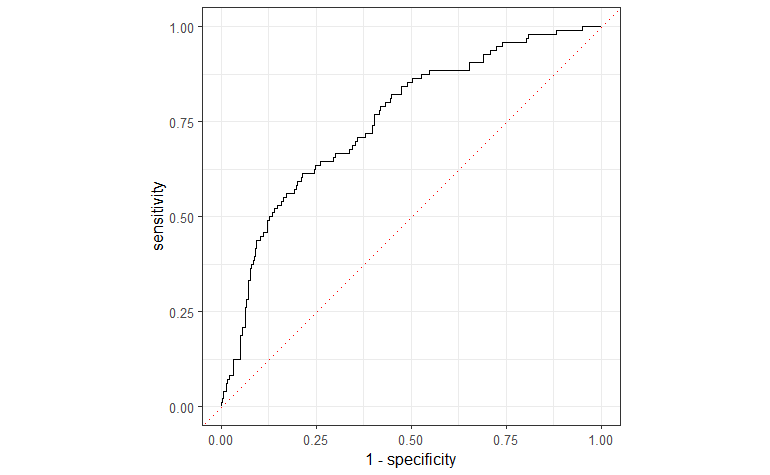フィッティングされたモデルのAUCは75.50%で、このモデルは予測可能性が高いことを示している。
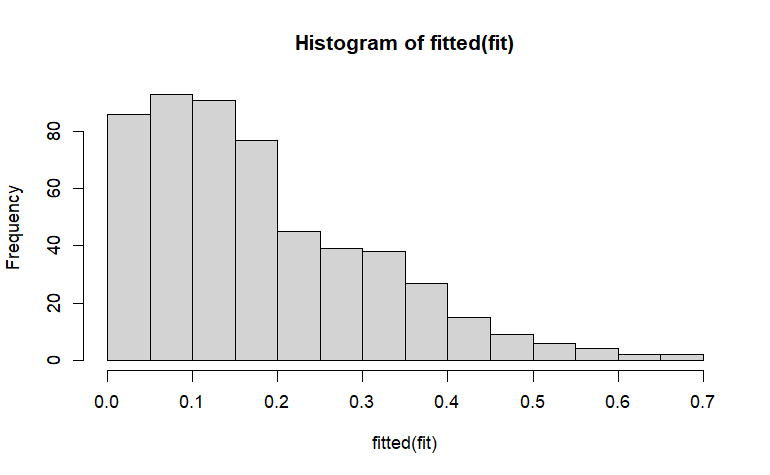
予測確率のヒストグラム Histogram of Predicted Probabilities
最後に、予測確率のヒストグラム（分類プロットとも呼ばれる）と結果は、予測の質を調べるために使用できる。このヒストグラムは、視覚的に有益なグラフで、偽陽性のパーセント、偽陰性のパーセント、および正しい分類のパーセントを提供する。よく区別された予測を示すために、分類プロットは、次の特徴を持つべきである：(1) U字形（正規分布よりもむしろ）、(2) ケースがそれぞれの端に集まっている（すなわち、カット・ポイントからより離れている、通常、二項ロジスティック回帰では0.5）、(3) 分類における最小のエラー（すなわち、わずかな偽陽性とわずかな偽陰性）。ヒストグラムは、正しい分類のパーセンテージとグループ間の分離をグラフィカルに描写することによって、分類率の測定を補足する。残念ながら、AUCがROC曲線を定量化するように、このヒストグラムに含まれる情報を定量化する単一の数値は存在しない。
hist(fitted(fit))
