重回帰の前提は下記のものである。
- 線形性 Linearity...予測変数と従属変数の残差間に線形関係が存在する。
- 正規性 Normality ...残差が正規分布する。
- 分散均一性 homoscedasticity ...残差は一定の分散を持つと仮定する
- 独立性 Independence...観測変数が互いに独立である(多重共線性がない)。
AERパッケージに含まれるCPS1985データで確かめてみよう。
library(AER) data(CPS1985)
head(CPS1985)
wage education experience age ethnicity region gender occupation sector union married 1 5.10 8 21 35 hispanic other female worker manufacturing no yes 1100 4.95 9 42 57 cauc other female worker manufacturing no yes 2 6.67 12 1 19 cauc other male worker manufacturing no no 3 4.00 12 4 22 cauc other male worker other no no 4 7.50 12 17 35 cauc other male worker other no yes 5 13.07 13 9 28 cauc other male worker other yes no
重回帰分析
mod <- lm(wage ~ gender + age + education, data = CPS1985) summary(mod)
前提条件の検証
QQプロットを作成する。 QQプロット(分位点-分位点プロット)のことであり、正規性の仮定を検証するために使用される。 あるデータ集合が正規分布や指数分布のような理論的分布に由来しているかどうかを評価するためのグラフである。例えば、残差が正規分布していると仮定して統計分析を行った場合、正規QQプロットを使ってその仮定をチェックすることができる。
QQプロットを作成するにはMosaicのqqmath関数を使用する。 点("p")と線("r")を追加するには、qqmath関数の引数にそれぞれを指定する。
library(mosaic)
qqmath(~resid(mod), type = c("p","r"))
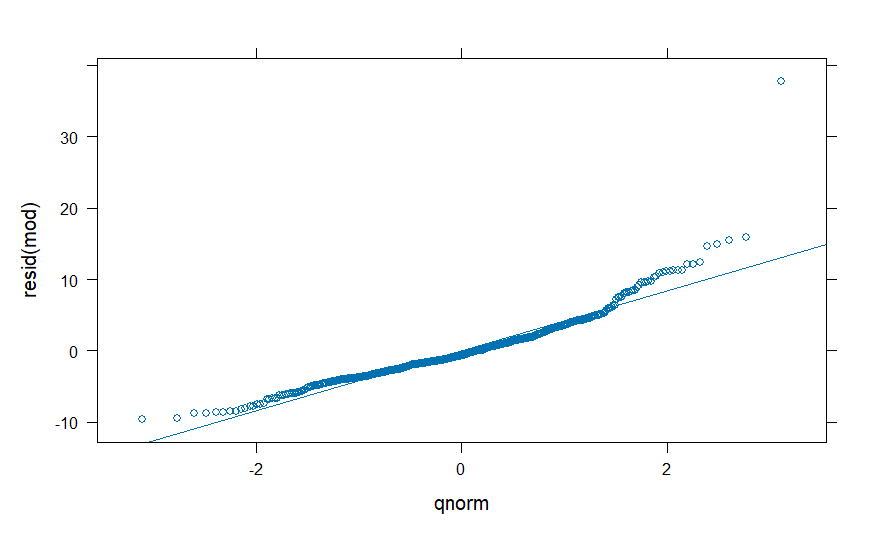
両端に外れ値があるものの、プロットの全体のフィッティングは非常によい。QQ-プロットから正規性の仮定が有効であることがわかる。
線形性と分散均一性の検証
フィット値プロットを得るにはネイティブのR plot関数を使用する。
plot(mod , which = 1)
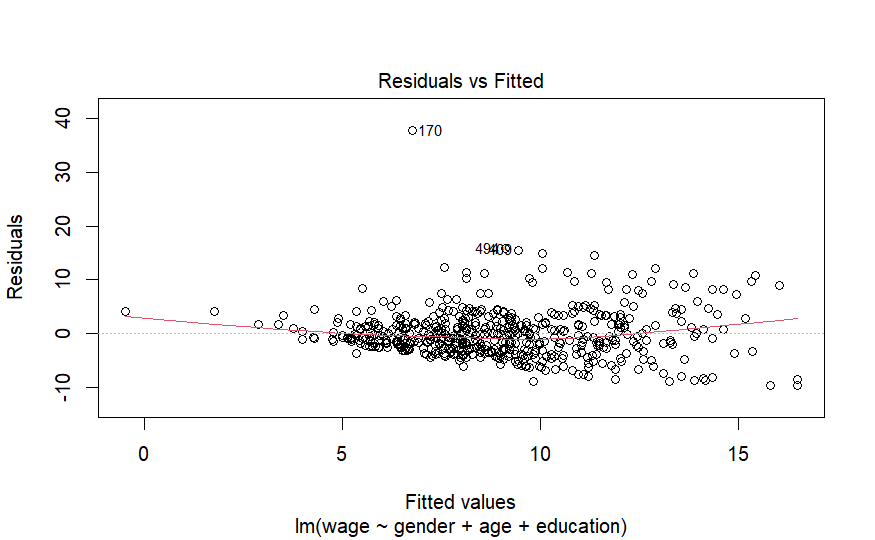
適合値プロットでは、(モデルを使った)適合値と残差を比較する。線形性の仮定が満たされている場合、適合値プロットは、ほぼ水平な適合線を持つことになる(たとえば、y=0を中心にランダムに散らばっている)。このプロットでは、赤い線が点線y=0にかなり近いことから、線形性の仮定を確認することができる。
分散均一性も同一のプロットでみる。残差と、残差対予測値(つまりフィッティング値)のプロットにおいて、残差と予測値の関数より広がっている場合に、分散均一性は仮定できない。
分散均一性を検討するのにはBreusch-Pagan検定を使う手がある。
Breusch-Pagan検定
計算ができるパッケージはいくつかある。ここでは、carとlmtestでやっておこう。
library(car) bp_test <- car::ncvTest(mod) print(bp_test)
Non-constant Variance Score Test Variance formula: ~ fitted.values Chisquare = 40.51078, Df = 1, p = 1.9553e-10
library(lmtest) lmtest::bptest(mod)
studentized Breusch-Pagan test data: mod BP = 9.1069, df = 3, p-value = 0.0279
帰無仮説は「残差は等しい分散で分布する」であり、p値が0.05より大きくなければならないため、Breusch-Pagan検定では分散均一性を仮定できない。
手続き的には分散均一性を仮定できない場合には、ロバスト推定を行うことになる。
ロバスト推定を行う
library(MASS) mod.robust <- rlm(wage ~ gender + age + education, data = CPS1985) summary(mod.robust)
Coefficients:
Value Std. Error t value
(Intercept) -4.6060 1.0236 -4.4999
genderfemale -2.3399 0.3192 -7.3297
age 0.1171 0.0137 8.5281
education 0.7701 0.0614 12.5448
Residual standard error: 3.543 on 530 degrees of freedom
このロバスト回帰モデルが、OLSモデルと比較して、データへのより良い適合を提供するかどうかを決定するために、各モデルの残差標準誤差を計算することができる。残差標準誤差(residual standard error: RSE)は,回帰モデルの残差の標準偏差を測定する方法であり、RSE の値が低いほど、モデルがデータに適合的である。
## OLSモデルの残差標準誤差を求める summary(mod)$sigma ## ロバスト推定したモデルの残差標準誤差を求める summary(mod.robust)$sigma
ロバスト回帰モデルのRSEは、通常の最小2乗回帰モデルよりも低い。これは、ロバスト回帰モデルがデータによりよく適合していることを示している。