lavaanなどのSEMパッケージでも回帰分析ができるとは以前から知っていたが、具体的にどうすればいいのか知らなかったので調べてみた。
シミュレーションデータ
AERパッケージの中のデータCPS1985を用いる。 賃金(wage)に対する効果を見る重回帰分析をデモに使う。独立変数は年齢(age)と教育年数(education)である。
重回帰
library(AER) data(CPS1985) lm01 <- glm(wage ~ age + education, data=CPS1985) summary(lm01)
結果は以下のようになる。
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.53423 1.27936 -4.326 1.82e-05 ***
age 0.10503 0.01718 6.112 1.90e-09 ***
education 0.82111 0.07705 10.657 < 2e-16 ***
ちなみに、重回帰分析は通常、最小二乗法OLSが推定法に使われている。
lavaanで重回帰分析を表現
次にlavaanで重回帰分析をしてみたい。
library(lavaan) model <- ' wage ~ 1 + age + education wage ~~ wage ' fit <- lavaan(model, data=CPS1985, estimator="ML") summary(fit)
1という数字を入れているのは切片は定数1からの影響を記述したものであるためである。 結果は以下のようになる。
Regressions:
Estimate Std.Err z-value P(>|z|)
wage ~
age 0.105 0.017 6.129 0.000
education 0.821 0.077 10.687 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
.wage -5.534 1.276 -4.338 0.000
estimatorをオプションで支持しているが、書かなくてもMLつまり最尤法が使われる。わかりやすいにように書いてみただけである。 推定値は最小二乗法の結果と同じだが、標準誤差とP値が異なっている。
最尤法は,データとモデルのズレを最小二乗法のように残差の2乗和ではなく、尤度という指標を用いて推定する。最尤法は.従属変数のデータが正規分布であることを仮定しているため、正規分布から外れる従属変数である場合には最尤法の推定は不正確になるという特性がある。
どちらの推定法の方が良いかというと、基本的には標準誤差が小さい方がよい方である。この場合は違いがないため、どちらの推定法でも変わらないと判断できる。
余談だがカテゴリカル変数を独立変数に入れると切片が違った値になる。これは重回帰分析でも同じでダミー変数はfactor()に囲って入れなければいけないのと同様である。ここで30分ほど躓いてしまった。
semplot
semPlotパッケージで描画するとこのようになる。
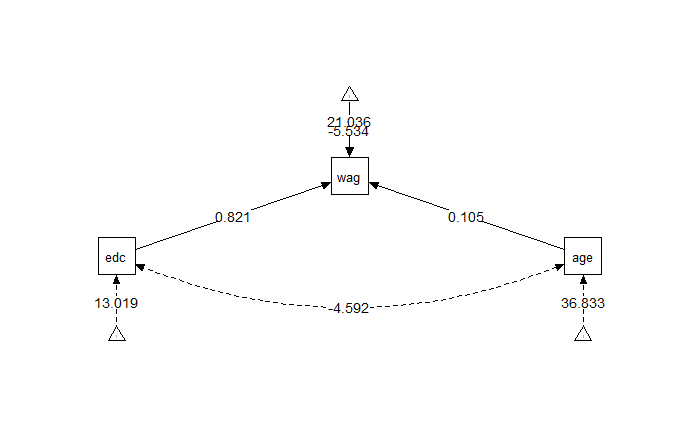
library(semPlot)
semPaths(fit, layout = "tree", shapeLat="ellipse", whatLabels = "est",
nDigits=3, shapeMan="square", sizeMan =6, sizeMan2= 10,
style = "lisrel", residScale=12, curve=2.5, edge.color="black",
rotation = 3, edge.label.cex=1)