2.9章から。
従来のCFAモデルでは、各指標・項目は理論的に仮定された1つの因子のみに負荷をかけ、項目の測定誤差は互いに相関しないとされている。つまり、局所独立の仮定である。これに応じてCFAでは交差因子負荷と項目の残差・誤差共分散は0に固定されている。理想的に言えば、各項目は理論的構成要素/因子の指標となるように設計され、局所独立性の仮定が成り立つ。しかし,実際の研究では,理論的な構成概念が完全な観測された指標・項目を持つことはあり得ない。観測された指標・項目は、通常、多かれ少なかれ、他の構成要素・因子とある程度の構成関連性を示し、その結果、仮説的な構成要素・因子に負荷をかけながらも、小さな交差因子負荷が可能となる(Marsh et al.2013; Marsh et al.2014; Sass and Schmitt 2010; Schmitt and Sass 2011)。CFAモデルにおいて、小さな交差因子負荷が存在するが無視される(つまり0に固定される)場合、結果として因子相関が上方に偏ることが研究で示されている(Stromeyer et al.2015; Marsh et al.2014; Asparouhov et al.2015)。しかし、CFAですべての交差負荷を解放することはできない。なぜなら、それはm2制限(mは因子の数)によるモデル同定問題を引き起こすからである(Muthén and Asparouhov 2012a)。
ベイズSEM(BSEM)(Muthén and Asparouhov 2012a; Asparouhov et al. 2015)モデルでは、交差負荷と残差共分散は,完全に0に固定されているわけでも,完全に自由であるわけでもなく,0に近似的に固定されている。そうすることでモデルはよりよくデータに適合する。BCFAでは、すべての項目が標準化され,因子分散が1に固定される。つまり、モデルはスケールフリーである。そのため、観測変数、潜在変数、および事前分布は一貫したスケーリングを持っている。Mplusで因子負荷量に使用されるデフォルトの事前分布はN(0, ∞)であり、プロビットリンクを使用する場合はN(0, 5)である。交差荷重に一般的に使用される先行値は,小分散正規先行値で,例えば,𝜆∼N(0, 0.01) (Asparouhov andMuthén 2010c)である。事前分布の平均値をゼロとすることは意味がある。交差負荷はゼロに近いが正確にはゼロではないと想定されるからである。事前分布の分散は、交差負荷の確実性についての理論や事前の信念に基づいています。0.01という小さな分散は、事前値の約95%がの事前値が-0.2から0.2の範囲にあることを意味する。異なる分散を持つ事前分布[例:𝜆 ∼ N(0, 0.001); 𝜆 ∼ N(0, 0.05)]を検討することもできる。
残差𝜃の行列に使われる事前分布は、交差負荷のものよりも複雑である。𝜃要素の事前分布は通常、逆ウィシャートIW(S, d)と仮定され、Sは共分散行列、dは逆ウィシャート分布の自由度である。Mplusで使用される共分散行列のデフォルトの事前分布はMplusで使用される共分散行列のデフォルトの事前分布は,連続変数の場合はIW(0, -p -1),カテゴリー変数やカテゴリーとpの組み合わせの場合はIW(I, p + 1)である。
変数,またはカテゴリー変数と連続変数の組み合わせの場合はIW(I, p + 1)である。観察される変数の数です。共分散行列での逆Wishartハイパーパラメータの指定についての詳細は, Asparouhov and Muthén (2010c) を参照。最近ではAsparouhov et al. (2015)が、以下の逆Wishartとして、よりシンプルに𝜃行列の事前分布IW(dD, d) を指定する方法を提案している。
サンプルサイズNが500程度であればd = 100から始め,Nが5000程度であればd = 1000から始めることができるとしている。モデル推定の収束が早く、PPP(posterior predictive p-value) > 0.05であれば、そのモデルは適切である。収束が遅いか、収束しない場合は、より大きなd値を用いてモデルを再実行する。モデル推定の収束が速いが、PPP < 0.05の場合は、より小さいd値を用いてモデルを再実行する。これはBSEMの感度分析とも呼ばれる(Asparouhov et al.2015)。異なるdの値を持つモデルがすべて高速で収束し、すべてのPPPが0.05以上である場合、dのより適切な値を決定する目的で、モデル比較にdeviance information criterion(DIC)を使用することができる。
本節では,図2.2に示したCFAモデルに基づいてBCFAを実装する方法を示す。BCFAでは,これらのパラメータを正確に0に固定するのではなく,ベイズ推定のための小さな事前分布を指定することによって,それらを近似的に0に固定するだけである。先に述べたように、BCFAにおける交差負荷の事前分布は、一般的に𝜆 ∼ N(0, 0.01)と指定される。残差𝜃行列のプライヤーは、通常、FIMLを用いたCFAの残差θ行列の推定値から計算されたDDPとして扱われる。Asparouhov et al.(2015)に従い、以下のMplusプログラムを用いてCFAから式(2.32)のd値を推定した。
Mplus Program 2.18
TITLE: BSI-18: Estimate residual data-dependent priors DATA: FILE =BSI_18.dat; VARIABLE: NAMES = X1-X18 Gender Ethnic Age Edu Crack ID; MISSING= ALL (-9); USEVARIABLES = Y1-Y18; DEFINE: Y1=X1; Y2=X4; Y3=X7; Y4=X10; Y5=X13; Y6=X16; Y7=X5; Y8=X2; Y9=X8; Y10=X11; Y11=X14; Y12=X17; Y13=X3; Y14=X6; Y15=X9; Y16=X12; Y17=X15; Y18=X18; STANDARDIZE Y1-Y18; ANALYSIS: ESTIMATOR=MLR; MODEL: SOM BY Y1* Y2-Y6; DEP BY Y7* Y8-Y12; ANX BY Y13* Y14-Y18; SOM@1; DEP@1; ANX@1;
すべての項目は標準化されており、因子分散は1に固定されている。後にBCFAのプログラムで残差パラメータのラベル付けを容易にするために、このプログラムで作成された指標変数y1~y18には,因子ごとに順番に番号が付けられている。本プログラムから推定された残差θ行列のパラメータは、式(2.32)で定義される残差𝜃行列のDDPを計算するために用いられる。そして、逆Wishart分布の自由度d = 100から始まるBCFAモデルを以下のMplusプログラムで実装する。
TITLE: BSI-18: Bayesian CFA DATA:
FILE =BSI_18.dat;
VARIABLE:
NAMES = X1-X18 Gender Ethnic Age Edu Crack ID;
MISSING= ALL (-9);
USEVARIABLES = Y1-Y18;
DEFINE:
Y1=X1; Y2=X4; Y3=X7; Y4=X10; Y5=X13; Y6=X16;
Y7=X5; Y8=X2; Y9=X8; Y10=X11; Y11=X14; Y12=X17;
Y13=X3; Y14=X6; Y15=X9; Y16=X12; Y17=X15; Y18=X18;
STANDARDIZE Y1-Y18;
ANALYSIS:
ESTIMATOR=BAYES;
PROCESSORS=2;
!CHAINS=2; !デフォルトのチェーンの数;
!POINT=MEDIAN; !default point estimate;
BITERATIONS=(10000); !総反復回数の最小値;
!FBITERATIONS=100000; !固定のベイズ反復回数を要求;
!KOLMOGOROV = 1000; !KS検定のためのチェーンを利用するデフォルト数;
!THIN=10; !各チェーンから10番目までのサンプル/ドローを保管;
MODEL:
SOM BY Y1* Y2-Y6
Y7-Y18(Sxload1-Sxload12);!minor loadings;
DEP BY Y7* Y8-Y12
Y1-Y6 Y13-Y18(Dxload1-Dxload12);!minor loadings;
ANX BY Y13* Y14-Y18
Y1-Y12(Axload1-Axload12);!minor loadings;
SOM@1; DEP@1; ANX@1;
Y1-Y18(RVar1-RVar18); !残差分散;
Y1-Y18 with Y1-Y18(RCVar1-RCVar153); !残差分散;
MODEL PRIORS:
Sxload1-Sxload12∼N(0,0.01); ! Prior for cross-loading;
Dxload1-Dxload12∼N(0,0.01);
Axload1-Axload12∼N(0,0.01);
!Prior for residual variance;
RVar1∼IW(50.2,100);
RVar2∼IW(64.6,100);
RVar3∼IW(46.8,100);
RVar4∼IW(50.5,100);
RVar5∼IW(66.8,100);
RVar6∼IW(43,100);
RVar7∼IW(31.7,100);
RVar8∼IW(42.5,100);
RVar9∼IW(22.4,100);
RVar10∼IW(45.7,100);
RVar11∼IW(67.5,100);
RVar12∼IW(85.6,100);
RVar13∼IW(50.9,100);
RVar14∼IW(47.8,100);
RVar15∼IW(53.6,100);
RVar16∼IW(51.1,100);
RVar17∼IW(53.8,100);
RVar18∼IW(57.9,100);
!Priors for residual covariance;
RCVar1-RCVar153∼IW(0,100);
OUTPUT: TECH8;
ベイズ推定量は、モデル推定のANALYSISコマンドで指定する。デフォルトでは、Mplusは2つの独立したマルコフ連鎖を用いてベイズ推定を行う。BITERATIONS=(10000)というオプションは、モンテカルロ・サンプリングの切り捨てを含めた最小10,000回の反復回数を意味する。BITERATIONSのデフォルトの最大反復回数は50,000回だが、FBITERATIONSではより多くの反復回数を指定することができる。事後分布に使用される反復回数(全反復回数の後半)は、収束がいつ起こるかによって決まる。ANALYSISコマンドのデフォルトオプションPOINT=MEDIANは、パラメータの点推定値が中央値であることを示している。POINTオプション(POINT=MEAN、POINT=MODEなど)を使用することで、デフォルトを変更できる。KOLMOGOROVオプションを使用すると,Kolmogorov-Smirnov(KS)検定のためのチェーンからのサンプル/ドローの数を指定できる.デフォルトでは、チェーン間の事後分布を比較するKS検定では、各チェーンから100個の事後サンプル/ドローが使用される。モンテカルロ標準誤差の偏りの原因となるMCMCにおけるサンプルの自己相関を減らすために、各チェーンのk番目のシミュレーションサンプルだけを残してマルコフチェーンを細分化するのが一般的な戦略である。Mplusのデフォルトでは、マルコフ連鎖の間引きは行われない。THIN=Kオプションを使用すると、事後分布からK個目のサンプルをすべて残すことができる。OUTPUTコマンドのオプションTECH8は、事後分布の収束性を評価するためのKS検定とPSR(potential scale reduction)を提供する。
Sxload1-Sxload12, Dxload1-Dxload12, Axload1-Axload12とラベル付けされた合計36個の交差負荷があり、MODEL PRIORS commandでそれぞれの交差負荷にN(0,0.01)の情報事前分布が指定されている。また,RVar1-RVar18とラベル付けされた18個の残差共分散があります.残留共分散の数は、[18(18-1)]/2 = 153で、それぞれRCVar1-RCVar153と表示されている。残差分散と共分散の情報量の多い事前分布は,IW(dD,d)分布で指定される.ここで,dは100に設定され,Dの値は残差分散/共分散のML推定値である.例えば、Mplus Program 2.18で推定された項目x1のCFA残差は0.502であり,IW事前分布で指定されたdDの値は0.502×100=50.2であるため,MplusプログラムのMODEL PRIORSコマンドでは、残差分散RVar1の情報的事前分布としてRVar1∼IW(50.25,100)が指定されている。他の残差分散の情報提供事前分布も同じように指定されている。CFA推定の残差共分散はすべてゼロなので、残差共分散のIWプライヤーは簡単で、18(18-1)/2=153のIWプライヤーがMODEL PRIORSコマンドでIW(0,100)と指定される。OUTPUTコマンドのTECH8オプションは、モデル推定の最適化履歴だけでなく、KS検定やPSRなどの収束情報を出力に表示することを要求している。
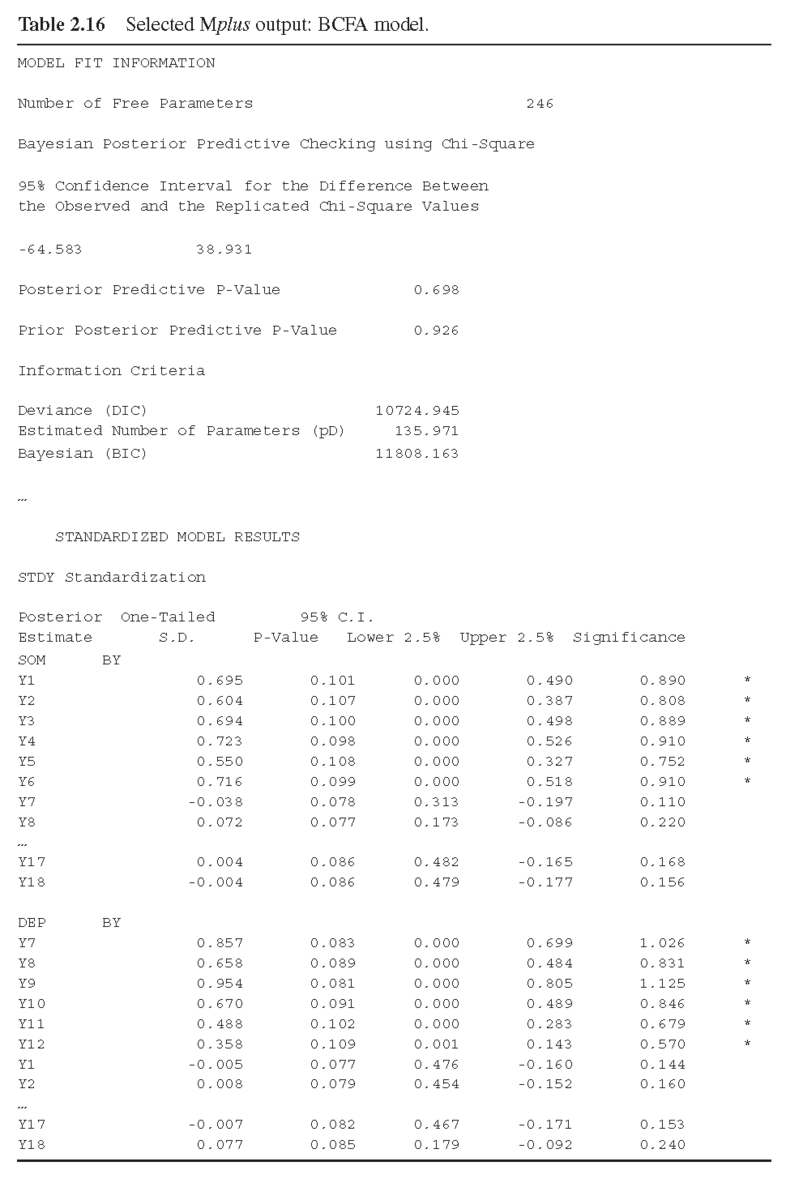
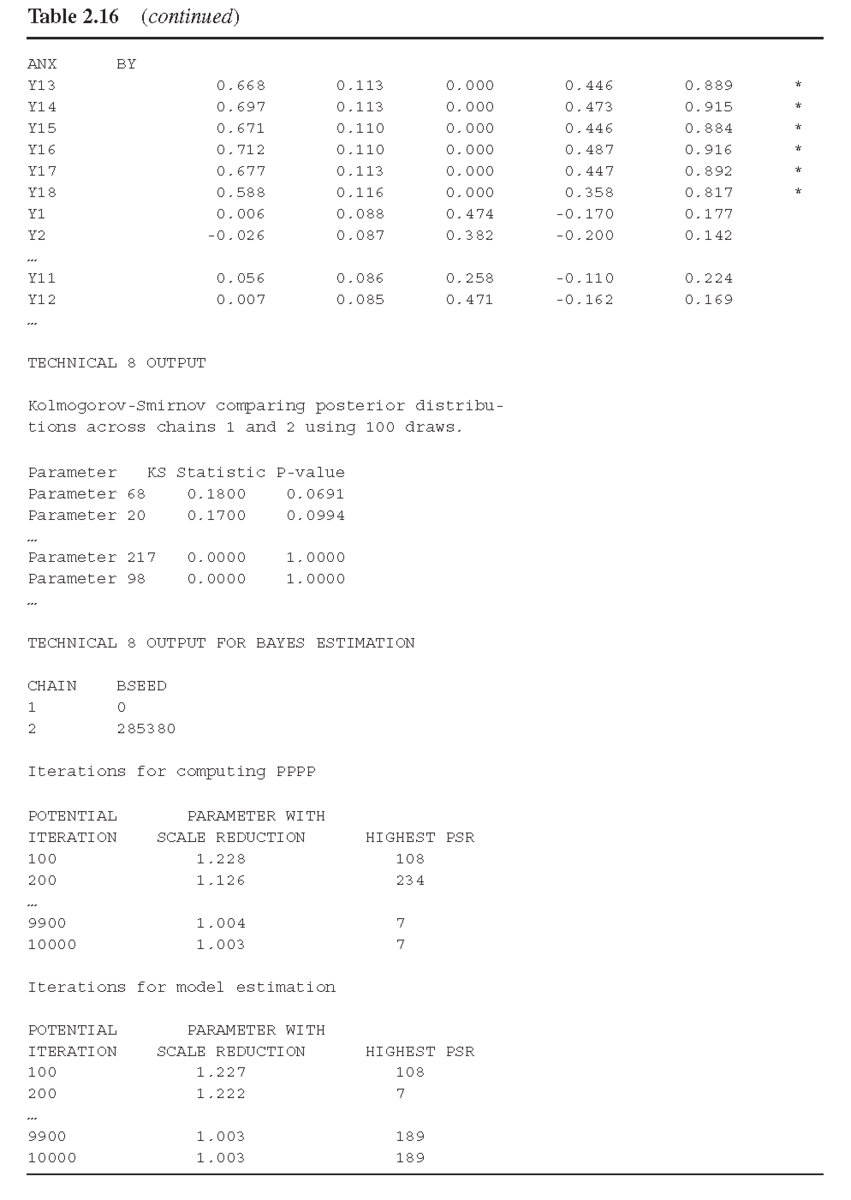
BCFA のモデル結果の抜粋を表 2.16 に示す。モデルの適合性を評価する前に,まずモデル推定の収束性を確認する。KS検定のp値はすべてのパラメータ推定値で0.05より大きく、異なるチェーンの事後分布が類似していること、またはシミュレーションが収束していることを示している。ただし、いくつかのパラメータのKS P値が小さく、TECH8の出力の「シミュレーションされた事前分布」に「不適切な事前分布」と表示される場合がある。これは「KSテストが厳しすぎるため、不適切な事前分布であっても適切な事後分布になる可能性があり、それがすべてである」(21)ため、無視することができる。モデル推定の収束性を評価するには、通常、PSRに注目する。この例では、10,000回の反復後、モデル推定における最高のPSRは、パラメータ189で1.003となり(表2.16の下段参照)(22) シミュレーションの適切な収束を示している(Gelman et al. 2004). Mplus 8は、TECH8オプションを指定すると、「PPPPを計算するための反復」(prior posterior predictive p-value)のPSRも提供する(Hoijtink and van de Schoot 2018; Asparouhov and Muthén 2017)。PPPPは、クロスローディングや残差分散・共分散など、特定のマイナーパラメータを対象とした検定である。現在のMplusのバージョンでは、PPPPは、残差分散/共分散ではなく、切片、斜面、因子負荷量の検定にのみ利用できる。この例のBCFAモデルでは、PPPPを計算する際の最高のPSRは、パラメータ7でPSR = 1.003となった。10,000回の反復を行った後、パラメータ7でPSR=1.003となり、マイナーパラメータ(交差負荷など)の推定にMCMC反復を行ったことを示している。マイナーパラメータ(この例では交差負荷)の推定のためのMCMCの繰り返しが適切に収束したことを示している。 モデル推定が適切に収束したことを確認した後、事後予測検査(posterior predictive checking : PPC)(Gelman et al.1996)を用いてモデルの適合性を評価する。モデルの 観測値とモデルで生成された𝜒2の値の差の95%CIはゼロ(-64.583, 38.931)をカバーし、PPPは0.698である。このモデルはデータによく適合していると結論づけている。PPPPは、Mplusの出力でも生成される。PPPP = 0.926の値は、N(0, 0.01)の仮説(すなわち、交差負荷に指定した事前分布)を棄却できないことを示している。言い換えれば、我々のモデルにおける交差負荷の推定値は、N(0, 0.01)分布の外側にはないということである。このモデルはデータによく適合しているので、逆Wishart分布の自由度ハイパーパラメータd=100を設定することは適切であると結論づけられる。感度分析のために,dの値を変えてモデルの推定を続けることができる(例:d = 50, d = 150, d = 200, ...).DICが最も小さくなるモデルがより好ましい。 モデルの結果は、すべての主要因子負荷量(すなわち,各項目の基礎因子に対する因子負荷量)が統計的に有意であり、従来のカットオフポイントである0.30よりも大きいことを示している。交差因子負荷やマイナー因子負荷は、いずれも統計的に有意ではない。すべての誤差相関は小さいが,いくつかの有意な誤差相関がある:rx1, x13 , rx2, x4 , rx5, x6 , rx5, x16 , rx7, x9 , rx10, x11 , rx11, x12 , rx12, x15 , rx15, x16(結果は表2.16では報告されていない). 本節では,Mplus で BCFA を実行することを示した。マイナー・パラメータ(交差因子負荷や残差共分散など)にマイナー変量情報プリアを追加することで、交差因子や残差共分散を0に固定するというCFAの厳格な枠組みを緩和することができる。CFAの適用において、モデルの適合性が低いのは、潜在的な交差負荷や特に誤差共分散に起因することが多い。このようなケースでは,より現実的な測定モデルであるBCFAを用いることで,データをよりよく適合させることができる。
21 Muthén (2015): http://www.statmodel.com/discussion/messages/11/12237.html?1485882536.
22 反復回数が少なければ、モデルの推定は速くなるが、PSRは反復回数を跳ね返す可能性があるため、PSRは収束を示す前兆かもしれない。収束を確認するために、MplusプログラムでFBITERATIONS=50000のオプションを使用して、50,000回の反復でモデルを再実行した。最も高いPSRは1.003で、収束が確認された。