Nylund、Asparouhov、Muthénの論文からnaive chi-square(NCS)、Lo–Mendell–Rubin、bootstrap likelihood ratio testの比較をした論文の結論部分。BLRTの優位性が示された論文として見かけることがあるが、あくまでもデータ次第であることが指摘されてことが抜け落ちていることが多いのではないかと思われる。
実践的に検定を用いていると、必ずしもBLRTが最適ではないケースに遭遇する。LMR、BIC、AICを示すことが必要になるだろう。
https://www.statmodel.com/download/LCA_tech11_nylund_v83.pdf
- Nylund, K. L., Asparouhov, T., & Muthén, B. O. (2007). Deciding on the Number of Classes in Latent Class Analysis and Growth Mixture Modeling: A Monte Carlo Simulation Study. Structural Equation Modeling: A Multidisciplinary Journal, 14(4), 535–569. https://doi.org/10.1080/10705510701575396
尤度に基づいた検定
表8は、3つの尤度ベースの検定(NCS、LMR、BLRT)の性能に関する情報を含んでいる。表7に示した結果と同様に、これらの結果は、一連のモデルについて、異なるクラス数での比較に基づいている。 これらの値を計算するために、各複製について、2クラスから6クラスのモデルを指定した結果のp値を調べた。なお、これらのLMRとBLRTでは、2クラスモデルを指定した場合、1クラスモデルと2クラスモデルを比較している。また、2クラスから6クラスの範囲の代替モデルを指定したことに注意。したがって、表8では、LCAモデルでは1クラスモデルから5クラスモデルまで、FMAモデルとGMMモデルでは1クラスから3クラスまでがLMRとBLRTの可能解となる。NCSについては、伝統的なカイ二乗分布を用いてp値を求める。このp値は,指定されたモデルとクラスが1つ少ないモデルとの間に有意な改善があるかどうかを評価するために使用される。これらのp値を見て、最初の有意でないp値(p > .05)の発生に基づいて選択されたモデルを特定した。.95に近い太字の数値は、テストが完璧に近いパフォーマンスを示したことになる。カテゴリ別LCA8クラスモデルのLMR列の太字の数値は、n=500 は,再現実験の78%が4クラスの解が正しいモデルであると結論づけたことを示している。
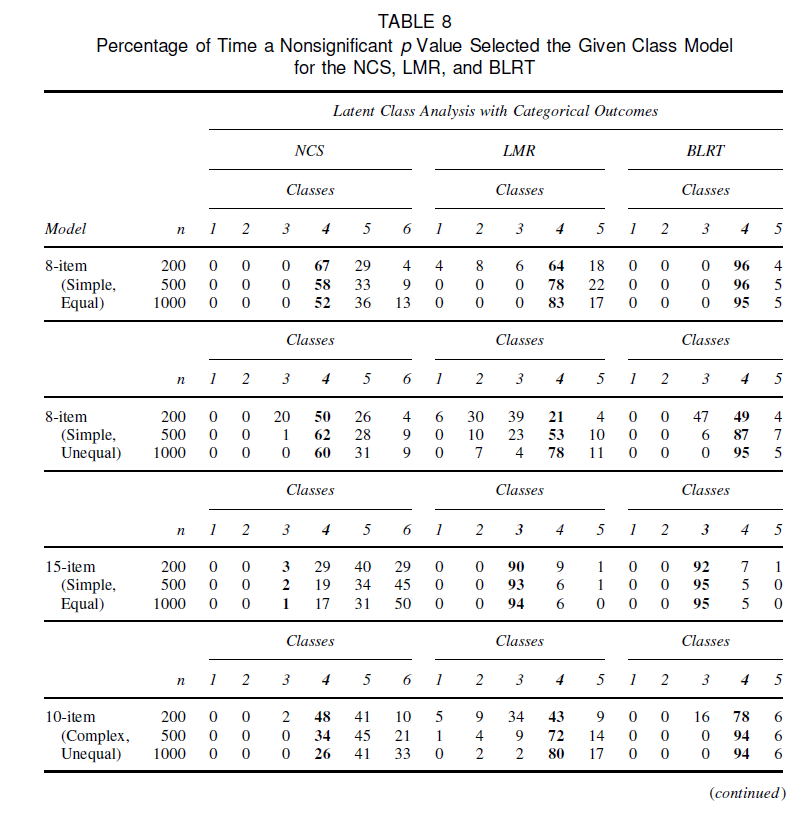
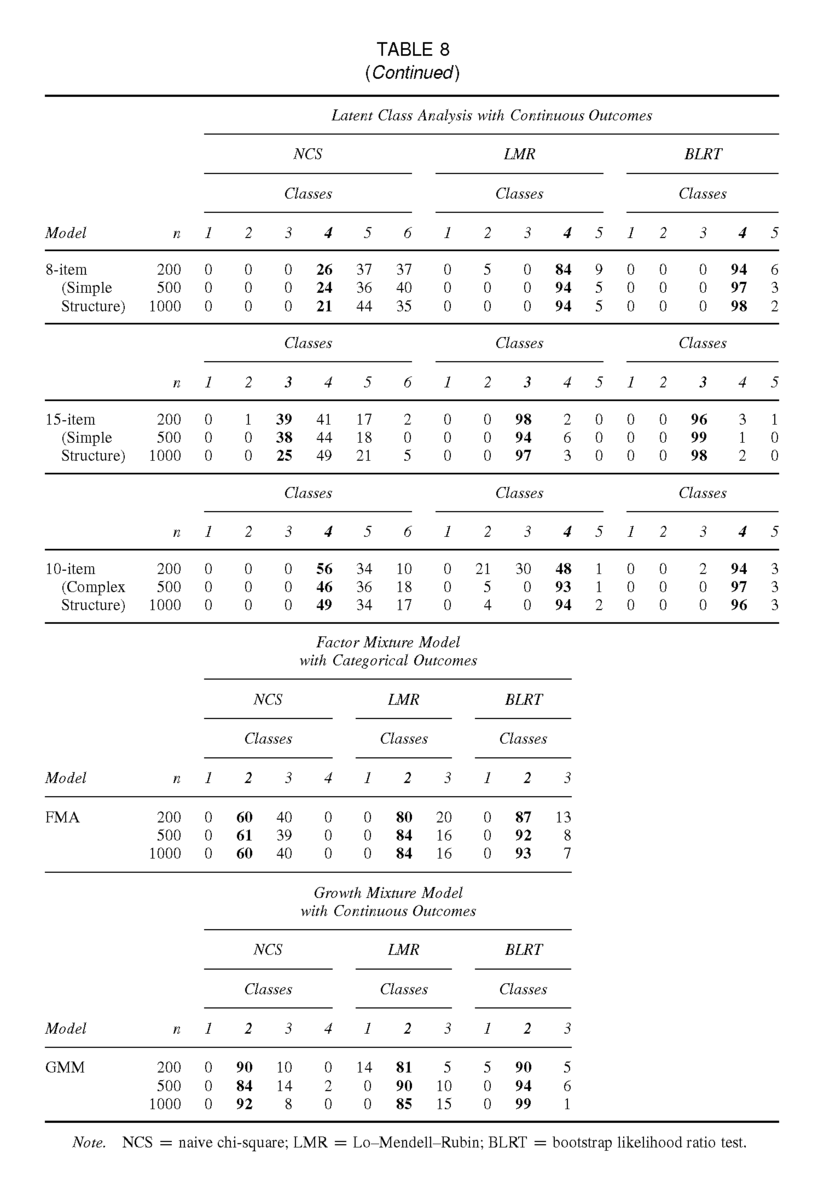
表8の結果は、NCSやLMRに対するBLRTの明確な優位性を示している。ほぼ全てのLCAモデルとサンプルサイズを考慮した場合、BLRTはほぼ95%の確率で真のkクラスモデルを正しく同定することができる。NCSを見て、LCAモデルを考慮すると、サンプルサイズが大きくなるにつれて性能が低下し、一貫して低いままであることに気づくま。FMAモデルでは、NCSの性能は一貫して低く、具体的には、すべてのサンプルサイズにおいて、正しいモデルを約60%の時間でのみ識別している。しかし、GMMモデルについては、BLRTほどではないが、NCSは一貫して良好な結果を示した。カテゴリー別LCA15項目モデルでは、LMRはBLRTとほぼ同等の性能を示し、90%から94%の確率でLMRは正しいクラス数を選択した。同じ設定において、NCSの性能は非常に低く、正しいモデルを識別できたのはせいぜい3%であった。連続的な結果を持つLCAモデルでは、LMRとBLRTはn = 500と1,000で非常に良い性能を発揮する。カテゴリカルと連続のLCAの両方において、15項目のモデルでは、LMRは、すべてのサンプルサイズにおいて、90%以上の正しい割合でモデルを同定し、むしろ良いパフォーマンスを示す。
このシミュレーションでは、3つの尤度検定(NCS、LMR、BLRT)と、カテゴリと連続の両方の結果を持つ混合モデルにおいてクラス数を決定するために使用される一般的な適合指標の性能について検討した。 我々は、これらのモデルにNCS検定を使用した場合、新たに提案されたLMRやBLRTと比較して、どの程度誤解を招くかを理解することに努めた。また、従来のIC指標についても検討した。
尤度に基づく検定の比較
本研究の結果は、k - 1 対 k クラスモデルの検定に NCS を使用した場合、真のモデルを棄却する頻度が高すぎるという事実を支持するものであった。NCSはサンプルサイズに特に敏感であり、LCAモデルについてはサンプルサイズが大きくなるにつれてその性能は実際に悪化することが指摘されている。前述したように、この検定は入れ子型混合モデルの検定には適していないことが分かっている。この仮定違反は、サンプルサイズが大きくなるにつれて増幅される可能性がある。表8で見られるように、NCSがうまくいかないとき、クラスの数を過大評価する傾向があることに注意することが重要である。NCSの代替として、他のLRTであるLMRとBLRTは、より正確に正しいモデルを識別する能力を有することが示された。BLRTはほぼ全てのモデリング設定において、LMRよりも明らかに優れた性能を示した。
NCSテストのType 1エラー率が高いので、LMRとBLRTの検出力の結果のみを考察する。本研究で検討したほぼすべてのモデルで、LMRとBLRTの両方が良好な検出力を有している。BLRTは、LMRよりも、すべてのサンプルサイズにわたって、より一貫した検出力を持つ。BLRTとLMRの検出力のわずかな差は,検出力(すなわち,kクラスとk - 1クラスのモデルを区別すること)の点で,2つのテストの性能に大きな差があることを示すものではない。
表 8 の LMR の結果を考慮すると、一般的に LCA モデルにおいて LMR がモデルを正しく認識できない場合、クラス数を過大評価する傾向があることがわかる。したがって、LMRをクラス列挙のツールとして使用する分析者は、LMRのp値が有意でない場合、最大でその数のクラスが存在すると確信することができるが、実際にはもっと少ないかもしれない。クラス数を過大評価することは、クラスを過小評価することよりも良いと考えることができる。なぜなら、k + 1クラスの解から真のkクラスの解を抽出することができるからである。例えば、真の解がk = 3で、モデルLMRが4クラス解を同定した場合、4クラス解のクラスの1つが実質的に意味をなさないか、同定が困難な非常に小さなクラスが存在する場合がある。その結果、LMRの結果にもかかわらず4クラス解を採用せず、真の3クラス解に落ち着くということもあり得る。しかし、LMRがあった場合、BICの優位性がより明らかになる。BICは修正BICよりも一貫して正しいモデルを識別し、修正BICはn = 200の8項目モデルで49%まで低下する。FMAとGMMの両方において、BICはうまく機能しており、最悪の場合、84%の確率で正しいモデルを識別することができる。これらの結果から、BICはクラス数を正しく特定するために検討されたICの中で最も整合的なICであると結論づけられる。表7より、BICはモデルの種類によらず、サンプルサイズが小さい場合に感度を持つことがわかる。 これらのICの性能に及ぼす構造の影響をより深く理解するためには、さらなる研究が必要であることは間違いない。
BICとBLRTの比較
表7と表8の結果を比較して、ICの中で最も性能が良いBICと、LRTの中で最も性能が良いBLRTの性能を理解することができる。カテゴリカルな結果を持つLCAでは、BICよりもBLRTの方が正しいクラス数を特定することに一貫性がある。なぜなら、最悪の場合、BLRTは49%の確率で正しいクラス数を特定するからである。これは、不等クラス、n = 200を持つ8項目のカテゴリ結果LCAモデルにおいて、最悪の場合、正しいクラス数を全く識別できないBICよりも優れている。連続的な結果を持つLCAを考慮すると、BICは良いパフォーマンスを示すが、n = 200に対して74%しか正しいモデルを同定することができない。この設定において、BLRTは一貫しており、94%の確率で正しいモデルを同定している。表7と表8の結果をFMAとGMMモデルについて比較すると、BICとBLRTはともに良好な結果を示している。この設定において、BICは最悪の場合、n = 200のGMMに対して84%の割合で正しいモデルを同定し、BLRTは最悪の場合、n = 200のFMAに対して87%の割合で正しいモデルを同定している。このように、本研究のすべてのモデルを考慮し、表7と表8の結果を比較すると、BLRTは正しいクラス数を示す最も一貫した指標として際立っていることがわかる。
ここで示した結果は、すべての混合モデルのごく一部であるが、FMA と GMM の結果は、それぞれ 1 つのモデルのみに基づいていることに注意することが重要である。したがって,表 7 と表 8 に示した結果を比較する場合,FMA と GMM の結果は LCA モデルほどには重視されない.Tofighi and Enders (2006) による最近のシミュレーション研究では,より広範な GMM モデルについて,クラス列挙の問題がより詳細に検討されている.
研究の結果をまとめると、BLRT テストは NCS や LMR と比較して明らかに有利であり、LCA モデルのクラス数を決定するための信頼できるツールとして使用できることが示された。BICは、LCAモデル、FMAおよびGMMモデルにおいて、検討した他のICよりもクラス数を正しく同定できることがわかった。LMRはNCSよりも良い性能を示したが、BLRTほどではなかった。もし、IC指標を一つ選ばなければならないとしたら、BICはクラス数の最も良い指標と思われるツールであろう。BLRTは、正しいクラスモデルを選択する一貫性から、LMRよりも選択されるであろう。全体として、すべてのモデルとサンプルサイズにわたって表7と8の結果を比較すると、BLRTは、この論文で検討したすべてのインデックスとテストの中で最もよく機能する統計ツールである。
しかし、BLRTには欠点もある。BLRTを使用した場合、我々の例では計算時間が5倍から35倍に増加したことに留意されたい。BLRTアプローチのもう一つの欠点は、分布とモデルの仮定に依存することである。複製されたデータセットは、推定されたモデルから生成され、モデルで使用されたものと正確な分布を持つ。そのため、モデルや変数の分布に誤った仕様があると、複製されたデータセットが元のデータセットと類似した性質を持たなくなり、誤ったp値の推定につながる。例えば、あるクラス内のデータが歪んでいるにもかかわらず、正規分布としてモデル化されている場合、BLRTのp値は不正確となる可能性がある。外れ値もまた、誤ったp値の推定につながる可能性がある。さらに、BLRTは現在、複雑な調査データに対応することができない。同様に、様々なICは、モデル、分布、サンプリングの仮定に依存する。一方、LMRはパラメータ推定値の分散に基づいており、様々なモデルや分布の仮定の下で頑健かつ有効であり、複雑な調査データに対応することができる。したがって、このような状況では、LMRが望ましいと考えられる。しかし、我々のシミュレーションは検定の頑健性を評価しておらず、このトピックに関するさらなる研究が必要である。
実践のための推奨事項
BLRTの計算時間が長くなるため、モデル探索の最初のステップではBLRTを要求しない方がよいかもしれない。その代わりに、BICとLMRのp値をガイドとして使って可能な解に近づき、いくつかのもっともらしいモデルが特定されたら、これらのモデルをBLRTを要求して再分析することができる。さらに、尤度の値は標準的な差の検定には使えないことが知られているが、尤度の実際の値は、次のようにクラス数を決定するための探索的診断ツールとして使用することが可能である。
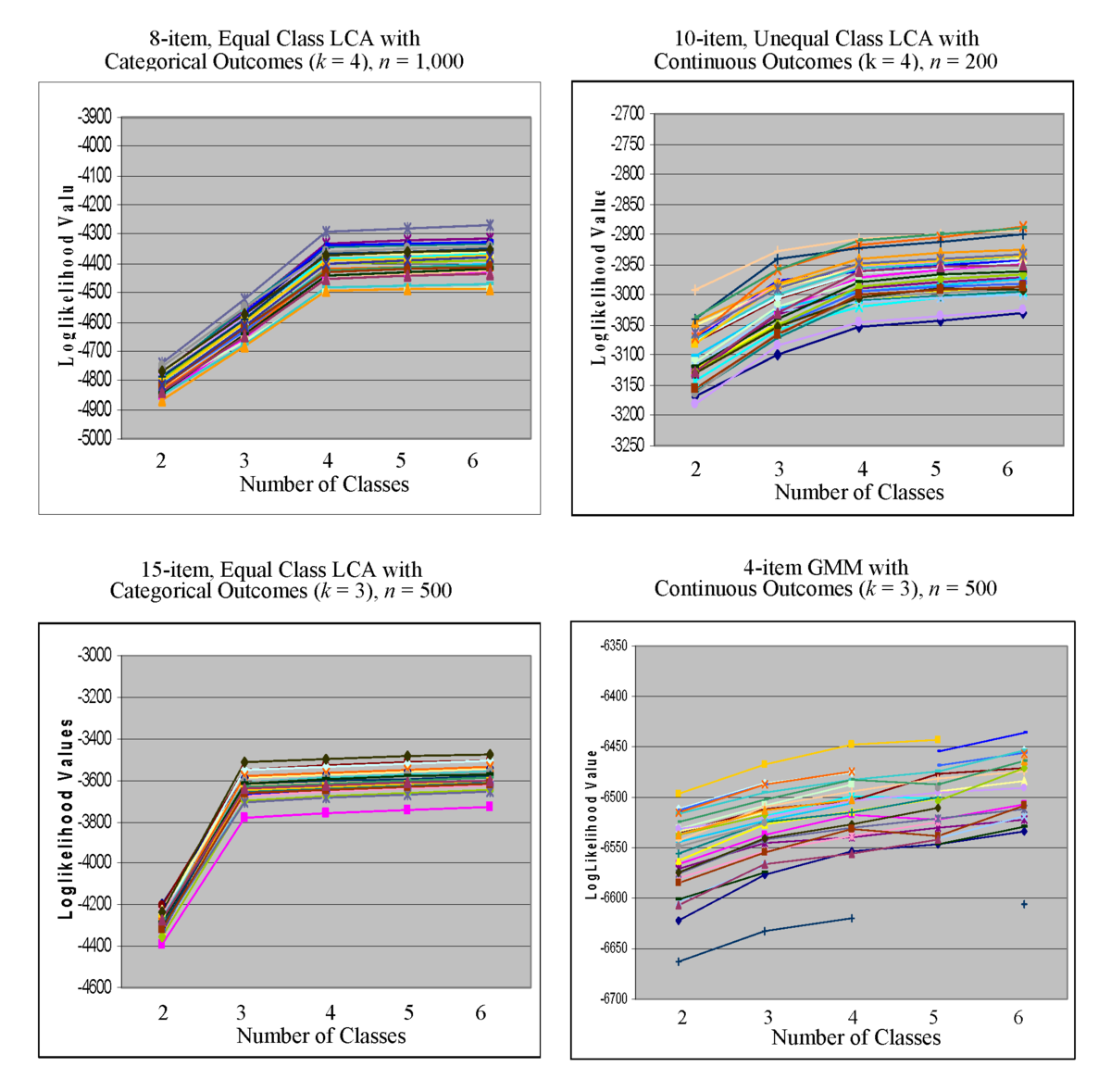
図5は、クラス数の異なるモデルについて、クラス数を決定するための説明変数として利用できる対数尤度値のプロットを4つ表示したものである。左上図は、8項目のLCAで、カテゴリ別の結果(n = 1,000)を見てみると、2クラスから3クラスに移るときに尤度が大きく増加し、3クラスから4クラスに移るときにも尤度が大きく増加するパターンがあることがわかる。そして、4クラスから5クラスに移るとき、また5クラスから6クラスに移るとき、同様に平坦になる。4クラスから5クラスの間で線が平らになっているのは、4クラスから5クラスになったときに、可能性が実質的に増加しないことを示唆している。さらに、8項目のモデルについては、それが真のk = 4クラスモデルであることが分かっているので、正しいポイントで起こる平坦化が観察された。ほぼすべてのモデリング設定において、同様のパターンが見られた。10項目、n = 200のモデルは、他のモデルほど劇的なフラットニングはありませんが、先に述べたように、これは最も難しいモデリング設定である。これは、GMMモデルのプロットでも観察される。4つのプロットしかないが、一般的な知見として、対数尤度プロットはn = 500とn = 1,000のLCAモデルに対してかなり一貫して正しいモデルを同定することが示唆される。従来の方法では、これらの対数尤度の値を差の検定のために検定できないことは分かっているが、このプロットは、クラス数を探索する際に尤度を記述的なツールとして使用する方法である。
本試験のモデルの選択により、特定のモデルおよびサンプルの属性が結果に及ぼす影響について結論が得られなかったことに留意することが重要である。例えば、単純構造モデルのような特定のタイプのモデル構造に対するこれらのテストとインデックスの性能について一般化することはない。むしろ、モデルやサンプルの選択は、LRTやICの性能を理解するために、様々な混合モデルを探求したいことが動機となっている。今後の研究では、モデルの構造、結果の性質(カテゴリーか連続か)、項目数との相互関係、クラスの列挙のための指標の性能をよりよく理解することを目指すことができる。
結論と今後の方向性
本研究では、混合モデリングにおける正しいクラス数を特定するためのICおよび尤度ベースのテストの性能について検討した。本研究で検討したツールの中で、結果は、BLRTが他のツールより優れていることを示した。2番目に良かったのはBICで、次いで修正BICであった。先行研究では、クラス数を決定するための様々な適合指標やテストが検討されているが、この論文は、この種の混合モデルに対するBLRT法の性能を詳細に検討した最初のものの1つである。限られた数のFMAとGMMモデルだけでなく、カテゴリと連続の両方の結果を持つLCAモデルを考慮することで、ICと尤度ベースのテストの性能の理解を、これまで検討されてきたものよりも拡大することができる。しかしながら、これらの結果は単なるプレビューに過ぎない。BLRTの有用性について広く述べる前に、より広い範囲のLCAモデル(例えば、共変数を含む、異なる構造のモデル、連続とカテゴリカルの結果の組み合わせなど)に対するBLRTとその性能についてより多くの研究を検討する必要がある。とはいえ、これらの結果は、これらの指標の性能をより深く理解することで、混合モデルにおけるクラス数の決定方法に関するさらなる理解に貢献するものである。