こちらの4章の翻訳。
https://cran.r-project.org/web/packages/PSweight/vignettes/vignette.pdf
4. NCDSデータによるケーススタディ
NCDS(National Child Development Survey)データを用いて、教育達成度の時間給への因果関係を推定するケーススタディにおいて、PSweightを実証する。4.1 節では、研究の概要を説明する。4.2節と4.3節では、それぞれ二値処理と三値処理の文脈における平均処理効果の傾向スコアによる重み付け分析を行う。セクション4.4では、傾向スコアと潜在的な結果に対する機械学習法がPSweightにどのように実装されるかを示す。
4.1. NCDS データ概要
NCDS(The National Child Development Survey)は、1958年にイギリス(UK)で生まれた子どもを対象とした縦断的な研究である(https://cls.ucl.ac.uk/cls-studies/1958-national-child-development-study/)。NCDSは17,415人の教育達成度、家族的背景、社会経済的・健康状態などの情報を収集した。Battistin and Sianesi (2011)に従って前処理を行い、1991 年に雇用された男性 3,642 人のうち、学歴と賃金情報が完全なサブセットを得て、分析を行った。 また、Multiple Imputation by Chained Equations (MICE, Buuren and Groothuis-Oudshoorn 2010) を用いて、欠損共変数をインプットし、1つのインプットデータセットを得て、その後のすべての分析に用いている*。
*我々が検討した治療前の共変量12個のうち10個に欠損Missingnessがある。最も小さい欠損の割合は4.9%で、最も大きい欠損の割合は17.2%である。我々は、説明のために1つの代入された完全なデータセットを考慮したが、より厳密な分析は、Rubinのルールによって複数の代入れたデータセットからの分析を組み合わせることによって進められることに留意されたい。
治療変数は教育達成度である。処理変数は学歴であり、二項治療の場合、学歴を取得したかどうかを示すDanyを作成した。学歴がある者は2399人であり、学歴がない者は1,243人である。複数回治療の場合、Dmultは3つのレベルで作成した。">=A/eq"と "O/eq"と "None"である。上級資格者(1,806人)、中級資格者(941人)、無資格者(895人)を表している。前処理の12の共変量または潜在的な交絡因子を考慮した。変数whiteは白人種であると自認しているかどうか、schtは16歳時に通っていた学校の種類、qmabとqmab2は7歳と11歳の時の数学テストの得点、qvabとqvab2は7歳と11歳の時の読解テストの点数、sib_uは兄弟の数、agepaとagemaは1974年の両親の年齢、同年には母親maempの雇用形態も収集、paid_uとmaid_uは両親の教育年数、agepaとagemaは1974年の親の年齢である。
研究変数に関する情報は、str()関数を用いて以下のように要約することができる。
library(PSweight) str(NCDS)
'data.frame': 3642 obs. of 16 variables: $ white : int 1 1 1 1 1 1 1 1 1 1 ... $ wage : num 2.57 2.04 1.72 2.2 2.48 ... $ Dany : int 1 1 0 1 1 0 0 1 1 1 ... $ Dmult : chr ">=A/eq" ">=A/eq" "None" "O/eq" ... $ maemp : int 0 0 0 0 1 1 0 1 0 1 ... $ scht : int 2 1 1 3 1 2 1 1 1 3 ... $ qmab : int 2 5 4 5 3 1 4 5 5 2 ... $ qmab2 : int 2 5 4 4 3 1 1 4 4 5 ... $ qvab : int 1 5 4 4 2 2 2 4 3 4 ... $ qvab2 : int 2 5 5 5 3 2 1 3 1 5 ... $ paed_u : int 9 0 0 10 9 10 0 11 10 10 ... $ maed_u : int 9 0 0 10 9 9 0 11 9 10 ... $ agepa : int 60 56 57 40 57 43 43 46 43 47 ... $ agema : int 59 56 53 41 45 42 38 45 43 40 ... $ sib_u : int 3 0 0 1 1 1 1 1 0 3 ... $ wagebin: num 1 0 0 1 1 0 1 1 1 1 ...
4.2. 二元的処置による傾向スコア重み付け
傾向スコアの推計とバランスチェック
学歴の取得が時間当たり賃金の上昇につながるかどうかの因果関係を推定したいとする。学歴の取得は無作為化されておらず、潜在的な交絡因子によって影響を受ける可能性があるため、以下の傾向スコアモデルを設定し、重み付け分析を行う。
ps.any <- Dany ~ white + maemp + as.factor(scht) + as.factor(qmab) +
as.factor(qmab2) + as.factor(qvab) + as.factor(qvab2) + paed_u + maed_u +
agepa + agema + sib_u + paed_u * agepa + maed_u * agema
共変量の主効果に加えて,Battistin and Sianesi(2011)に従って,親の年齢と教育の交互作用を調整することを検討した。Sumstat()関数を用いてロジスティック傾向スコアモデルを推定し、IPW、処理重み、OWの3種類の重み付けスキームにおけるバランス統計量を求めた。
bal.any <- SumStat(ps.formula = ps.any, data = NCDS,
weight = c("IPW", "overlap", "treated"))
Sumstat() 関数からの画面上の出力は、重みの選択と、重み引数に "treated" が含まれる場合にのみ選択される治療グループ (trtgrp) である。 この例では、trtgrpが指定されていないので、Sumstats()は自動的に処理変数のアルファベット順の最後のレベルを処理グループとする。Dany = 1.
bal.any
trt group for PS model is: 1 weights estimated for: IPW overlap treated
SumStatは,治療群レベル(ATTを定義するため)("trtgrp"),推定傾向スコア("propensity"),各重み付けスキームにおける推定重み("ps.weights"),有効サンプルサイズ("ess"),各重み付けスキームにおけるバランス統計(例: "unweighted.sumstat", "IPW.sumstat", "overrap.sumstat", "treated.sumstat")などを含むリストとして返される。さらに、各重み付けスキームのバランス統計は、共変量の非重み付け標準偏差または重み付け標準偏差の両方と、ASDとPSDの両方を含んでいる。
plot.SumStat()関数は、推定傾向スコアと共変量balance統計量の分布を可視化する。引数type = "hist"を指定すると、処置(trtgrpで定義される治療)を受ける推定傾向スコアのヒストグラムが生成される。
また、type = "density"は、各治療水準を受ける推定確率の密度を示す。図1は、我々の分析における推定傾向スコアのヒストグラムと密度プロットである。ヒストグラムは、2つのグループの軽微な分離のため、重複がわずかに欠けている可能性を示唆している。
plot(bal.any, type = "density") plot(bal.any, type = "hist")
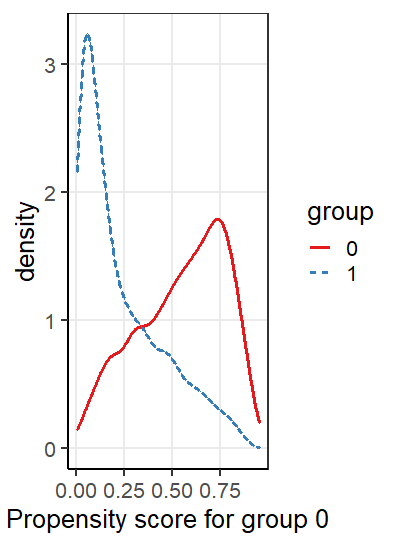

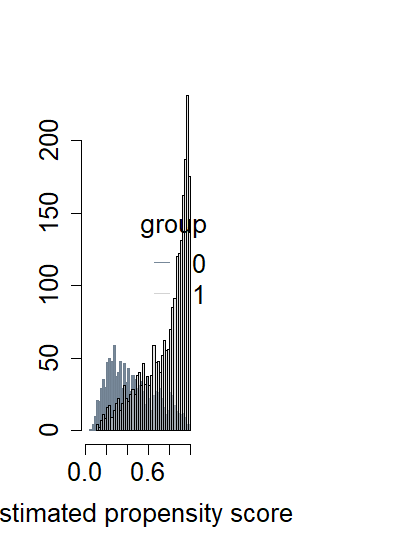
図1:plot.SumStat()関数で生成した二元処置変数Danyに関する推定傾向スコアのヒストグラムと密度プロット
最後に、plot.SumStat()で引数type = "balance"を指定すると、ASDメトリック(metric = "ASD")または最大PSDメトリック(metric = "PSD")に基づいたラヴプロットが生成されます。図2は、重み付き標準偏差(デフォルトではweighted.var = TRUE)を用いたPSDベースのラブプロットを示している。明らかに、重み付けされていない平均の乖離は、一般的に使用されるバランス閾値0.1よりも大幅に大きく、一方で傾向スコア重み付けは一般的に共変量バランスを改善することができる。 3つの重み付けのうち、OWとIPWは各共変量の最大PSDが0.1以下になるように制御されており、OWは各共変量の最大PSDが0に近く、最もバランスが取れていると言える。
plot(bal.any, type = "balance", metric = "PSD")

図2:PSweightパッケージのplot.SumStat()関数で生成した、最大PSDメトリックを用いたバイナリ処理変数Danyのラブプロット
加重平均治療効果の推定と推論
図2によれば、IPW、治療重み、OWは適切なバランスを保っているので、これら3つの重み付けスキームを用いて、ATE、ATT、ATOを推定する。傾向スコアモデルps.anyに基づき、まずPSweight()関数を用いてIPWを用いた結合集団の平均潜在的転帰を求める。
ate.any <- PSweight(ps.formula = ps.any, yname = "wage", data = NCDS,
weight= "IPW")
ate.any
Original group value: 0, 1 Point estimate: 1.9002, 2.0927
ate.anyは、PSweight()関数によって返されるPSweightオブジェクトである。 ate.anyをprintすると、各処理水準における潜在的な成果の推定平均値のみが得られる。この場合、1.9002 と 2.0927 は、全人口が学歴を持たない場合(Dany = 0)と持たない場合(Dany = 1)の平均対数時間給に相当する。学歴が高いほど平均時給が高くなることがわかる。そのシンプルな画面出力にもかかわらず、ate.anyは、推定傾向スコア(propensity)、推定平均潜在成果(muhat)、推定平均潜在成果の共分散行列(covmu)、bootstrap = TRUEの場合の各 bootstrap標本の推定値(muboot)、アルファベット順のグループラベル(group)、ATTを定義するための指示治療群(trtgrp)の、6要素の一覧から成っている。
PSweight()関数でweightオプションを指定することで、治療集団と重複集団の間の平均的な潜在的成果を同様の方法で推定することができる。 weightが指定されていない場合、PSweight()関数はデフォルトでOWを使用し、最適な内部妥当性を持つ部分母集団をエミュレーションする(Li et al. 2018). ウェイト = "treated "の場合、学歴のある母集団における潜在的成果の平均値を推定して得る。ATTを推定するために、trtgrpを無指定にすると、PSweight()関数はデフォルトで、ATTをdefiingする際に治療変数の最後の値(アルファベット順)を治療グループとみなす(Dany = 1)。 もし、学歴のない母集団での因果関係を推定したい場合は,trtgrp = 0 を指定する必要がある。
ato.any <- PSweight(ps.formula = ps.any, yname = "wage", data = NCDS)
att.any <- PSweight(ps.formula = ps.any, yname = "wage", data = NCDS,
weight = "treated")
ato.any
Original group value: 0, 1 Point estimate: 1.8617, 2.0408
att.anyの画面出力には、ate.anyやato.anyと比較して、ATT推定値を決定する処置群という要素が含まれている。NCDSデータの分析では、3つの対象集団の平均的な潜在的成果の推定値にわずかな差異が見られるだけであった。 例えば、母集団レベルの効果的な教育介入によって、いずれかの母集団に属するすべての人が学歴を獲得した場合、対数時給の平均値は一貫して高くなるようである。デザインモジュールと同様に、治療効果の加重平均とその分散を推定するためのsummary.PSweight()関数を提供する。
ate.anyおよびato.anyと比較して、att.anyの画面上の出力には、ATT推定値を定義する処置グループであるextra要素が含まれるようになった。NCDSデータの分析では、3つの対象集団における推定平均潜在的転帰の間にわずかな違いしか見られない。平均時間当たりログ賃金は、いずれかの対象集団のすべての個人が、例えば何らかの効果的な集団レベルの教育的介入を通じて学術的資格を獲得した場合、一貫して高くなるように見える。設計モジュールと同様に、概要を示す。PSweight () 関数を使用して、治療効果 (加重平均) とその分散を推定する。既定では、summaryのようになる。PSweight () は、推定された平均の潜在的な結果のtype="DIF")のすべての対ごと対比を示したものであり、したがって、追加の因果的な推定値を対象としている。たとえば、次のコードを使用して、ATEとATO、およびそれらのサンドイッチ標準誤差と95%信頼区間を推定できる。
summary(ate.any, CI = FALSE)
Closed-form inference:
Original group value: 0, 1
Contrast:
0 1
Contrast 1 -1 1
Estimate Std.Error z value Pr(>|z|)
Contrast 1 0.192543 0.021122 9.1158 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
summary(ato.any, CI = FALSE)
Closed-form inference:
Original group value: 0, 1
Contrast:
0 1
Contrast 1 -1 1
Estimate Std.Error z value Pr(>|z|)
Contrast 1 0.179129 0.015609 11.476 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
サマリーの戻り値。PSweight () 関数は, ATOの標準誤差がより小さく,関連する信頼区間がよりタイトであり, Liら (2018) の理論的結果と一致することを示す。概要。またPSweight ()関数は、指定された平均の可能性のある結果のコントラストが0であるという弱い帰無仮説のp値を返す。この場合, p値はH_0に対応し,[tex: H{0}=\mu{1}^{n}=\mu_{0}^{n}]はすべて小さく,帰無仮説を棄却する。
傾向スコアモデルを特定することに加えて,各治療群内の潜在的交絡因子の関数として時間給の対数に対するモデルを特定することにより拡張推定量を得る。PSweight ()関数を使用すると、傾向スコアの重み付けと結果のモデリングを組み合わせて、効率性や堅牢性の向上を実現できる。ps.anyで調整されたのと同じ交絡子のセットを使用して、out.formulaを通じて回帰式を指定する。
out.wage <- wage ~ white + maemp + as.factor(scht) + as.factor(qmab) + as.factor(qmab2) + as.factor(qvab) + as.factor(qvab2) + paed_u + maed_u + agepa + agema + sib_u + paed_u*agepa + maed_u*agema
処置変数はout.wageには含まれないが、これは、PSweightが各処置群内の個別の潜在的転帰回帰モデルに自動的に適合するためであり、したがって、完全な処置-共変量相互作用が可能となる。連続成果賃金の場合、PSweight () は既定で線形モデルに適合する (family="gaussian") 。結果回帰式を読み込み、augmentation=TRUEを指定すると、セクション2.4で導入された拡張重み付け推定器によって推定された平均の潜在的結果が得られる。
ate.any.aug <- PSweight(ps.formula = ps.any, yname = "wage", data = NCDS,
weight= "IPW", augmentation = TRUE, out.formula = out.wage)
ato.any.aug <- PSweight(ps.formula = ps.any, yname = "wage", data = NCDS,
augmentation = TRUE, out.formula = out.wage)
単純な重み付け推定量と同様に、画面上の出力には、処置群レベルの情報に加えて、それぞれの対象集団における推定された潜在的転帰の平均 (簡略化のために出力を省略) が含まれる。この解析では,検討中の各重みづけ方式に対して,単純重みづけ推定器と拡張重みづけ推定器との間で点推定が実質的に異ならないことを見出した。増強された加重推定値が単純な加重推定値に類似しているという事実は、傾向スコアモデルが大きく誤って特定されていないことの間接的な証拠となる可能性がある (Robins and Rotnitzky 2001; Mercatanti and Li 2014) 。
次に,要約を用いて (加重) 平均治療効果を推定した。PSweight ()関数。この例では、点推定値は、増大重み推定器と単純重み推定器との間で実質的に変化しないが、結果増大は、ATEを推定するための標準誤差を低減するが、ATOを推定するための標準誤差はそれほど大きくない。このような比較結果はMao et al. (2018)のシミュレーション結果と一致する。全体として、考慮された重み付けスキームにかかわらず、平均して学業資格を達成することは、0.05年レベルでないよりも有意に高い時間給につながることがわかった。しかしながら、我々は、研究結果の解釈が0.05より大きいか小さいp値の単一の二分法に依存すべきでないことを認めている。
summary(ate.any.aug, CI=FALSE)
Closed-form inference:
Original group value: 0, 1
Contrast:
0 1
Contrast 1 -1 1
Estimate Std.Error z value Pr(>|z|)
Contrast 1 0.186079 0.019842 9.3782 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
summary(ato.any.aug, CI = FALSE)
Closed-form inference:
Original group value: 0, 1
Contrast:
0 1
Contrast 1 -1 1
Estimate Std.Error z value Pr(>|z|)
Contrast 1 0.180004 0.015646 11.505 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
あるいは、標準誤差および信頼区間は、ノンパラメトリックブートストラップを介して推定することができる。たとえば、PSweight () 関数でbootstrap=TRUEを指定し、summaryを使用できる。PSweight () を使用して、平均の潜在的な結果に基づいて、因果的なコントラストのブートストラップベースの推論を行う。デフォルトでは、ブートストラップ複製の数は50に設定されており、PSweight () 関数でR引数を使用して他の値を指定できる。bootstrap=TRUEの場合、PSweight () は50回実行するごとに短いメッセージを出力し、監視を容易する。
ate.any.bs <- PSweight(ps.formula = ps.any, yname = "wage", data = NCDS,
weight= "IPW", bootstrap = TRUE)
表示
bootstrap 50 samples
画面上の出力であるate.any.bsは、ate.anyと同じだが、ate.any.bsを要約すると、ブートストラップ標準誤差、 (分位値ベースの) 信頼区間、および関連するp値が返されるようになった。次のコードを使用して、これらの情報を取得する方法を説明する。
summary(ate.any.bs, contrast = rbind(c(-1, 1),c(1, -1)))
Use Bootstrap sample for inference:
Original group value: 0, 1
Contrast:
0 1
Contrast 1 -1 1
Contrast 2 1 -1
Estimate Std.Error lwr upr Pr(>|z|)
Contrast 1 0.192543 0.021948 0.149661 0.22636 < 2.2e-16 ***
Contrast 2 -0.192543 0.021948 -0.226364 -0.14966 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
上記の例では、contrast 引数でデフォルトでない対照を指定できることをさらに説明している。contrast = rbind(c(-1, 1),c(1, -1)) とすることで、Dany = 1 対 Dany = 0 の因果比較とその逆比較を同時に報告することができる。この2つの対比は、同じ因果関係を2つの逆方向から研究しているので、同じ数値が逆符号で返されることが期待される。 ブートストラップ標準誤差はサンドイッチ標準誤差とほぼ同じであるが、ブートストラップ信頼区間は正規近似に依存しないため、点推定値に対して対称でなくなる。