回帰分析をplot()関数に入れたときに示されるプロットの一つであり、Y軸に残差,X軸に適合値(推定応答)をとって散布図にしたものである。このプロットは、非線形性、分散不均一性、外れ値などを検出するために使用される。
mtcarsデータを用いたデモ
model <- lm(mpg ~ wt + cyl, data = mtcars) summary(model)
plot(model)
residuals vs. fitted valuesと書かれたプロットである。

Faraway-Glen_bによる説明
StatsEexchangeでの議論を見てみよう。
ここでは、FarawayのLinear Models with Rのケースが引用されている。
 初版59ページ、第2版74ページにある。
初版59ページ、第2版74ページにある。
以下は、これらの残差プロットで、適合した(したがってxの)各値における点のおおよその平均と広がり(ほとんどの値を含む限界)を、条件付き平均(赤)および条件付き平均±(おおよその)条件付き標準偏差の2倍(紫)を示すおおよその概算でマークしたものである。
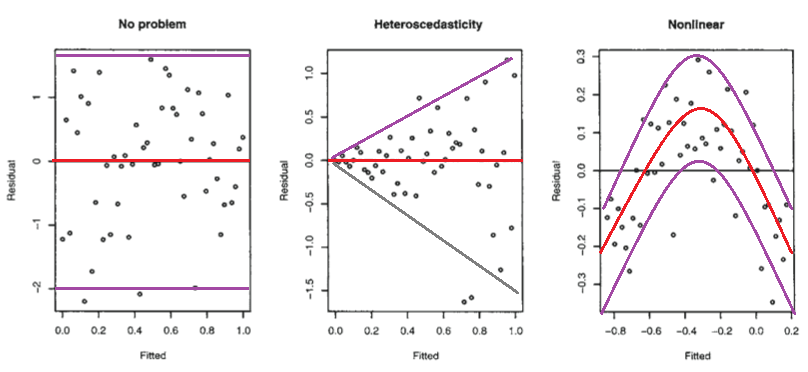
2番目のプロットは、平均残差は適合値によって変化しないが(したがってxによって変化ない)、残差の広がり(したがって適合線に対するyの広がり)は適合値(またはx)が変化するにつれて大きくなっているつまり、広がりは一定ではなくい。つまり、分散不均一性 Heteroskedasticity がみられる。
残差はフィット値が小さいときはほとんど負で、フィット値が中間のときは正、フィット値が大きいときは負であることを示している。つまり、広がりはほぼ一定であるが、条件付き平均はそうでない。関係が曲線的であるため、フィットした線はxが変化したときにyがどのように振舞うかを説明していない。
そうではない*。そのような状況では、プロットは3番目のプロットと異なって見える。
(i)誤差が正規分布だがゼロに中心がなく、θに中心がある場合、切片は平均誤差を拾うので、推定切片はβ0+θの推定値となる(これが期待値となりますが、誤差を含んで推定される)。その結果、残差はまだ条件付き平均0となり、第1のプロットのようなる。
(ii) 誤差が正規分布でない場合、点のパターンは中心線以外のどこかで最も密になるかもしれない(データが歪んでいた場合)。

ここでは、紫色の線はかなりおおよそ95%の区間を表しているが、もはや対称的ではなくなっている。(ここで基本的な点が不明瞭にならないように、いくつかの問題を無視している)。
*もし、本当に誤差のように振舞わない「誤差」項があれば、例えば、xとyがちょうどよい方法でそれらに関連していれば、これらのようなパターンを作り出すことができるかもしれない。しかし、誤差項については、例えば、xと関係がないとか、平均がゼロであるとか、そういう仮定をしているわけで、それを実行するには、少なくともそういう仮定をいくつか破らなければならない。(多くの場合、そのような影響はないか、少なくとも比較的小さいはずだと結論づける理由があるかもしれない)。
ggplt2での描画
library(ggplot2)
plot<-ggplot(model, aes(.fitted, .resid))+geom_point()
plot<-plot+stat_smooth(method="loess")+geom_hline(yintercept=0, col="red", linetype="dashed")
plot<-plot+xlab("Fitted values")+ylab("Residuals")
plot<-plot+ggtitle("Residual vs Fitted Plot")+theme_bw()
plot

