通常の頻度統計で行う。
library(AER) # CPS1985 データを含むパッケージ
data("CPS1985", package = "AER")
fit.freq <- lm(wage ~ age, data = CPS1985)
print(fit.freq)
結果。
Call:
lm(formula = wage ~ age, data = CPS1985)
Coefficients:
(Intercept) age
6.16747 0.07755
ベイズ統計での計算
単回帰のstanファイルを作る
data {
int<lower=0> N; // データポイントの数
vector[N] X; // 独立変数(年齢)
vector[N] Y; // 従属変数(賃金)
}
parameters {
real alpha; // 切片
real beta; // 傾き
real<lower=0> sigma; // 誤差の標準偏差
}
model {
Y ~ normal(alpha + beta * X, sigma); // 線形回帰モデル
}
このコードを"simple_linear_regression.stan"という名前で保存する。
以下はRコード。
library(rstan)
library(AER) # CPS1985 データを含むパッケージ
# CPS1985データを読み込み
data("CPS1985", package = "AER")
cps_data <- CPS1985
# 単回帰分析用のデータを準備
Number <- nrow(cps_data)
age <- cps_data$age # 年齢
wage <- cps_data$wage # 賃金
# Stanモデルのデータリスト
stan_data <- list(N = Number, X = age, Y = wage)
# Stanモデルを読み込み
stan_model <- stan_model("simple_linear_regression.stan")
# モデルのフィッティング
fit <- sampling(stan_model, data = stan_data, iter = 2000, chains = 4, seed=1234)
# 結果の表示
print(fit)
2000回のイテレーションと4つのチェーンを指定している。
収束診断
print(fit) check_hmc_diagnostics(fit) # HMC診断
Inference for Stan model: simple_linear_regression.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
alpha 6.18 0.02 0.72 4.77 5.69 6.16 6.66 7.60 1385 1
beta 0.08 0.00 0.02 0.04 0.06 0.08 0.09 0.11 1388 1
sigma 5.08 0.00 0.15 4.79 4.97 5.08 5.18 5.38 1956 1
lp__ -1131.94 0.03 1.23 -1135.00 -1132.44 -1131.63 -1131.06 -1130.59 1392 1
Samples were drawn using NUTS(diag_e) at Tue Apr 09 21:12:56 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
サマリー統計の解釈
- 平均(mean): 各パラメータ(alpha, beta, sigma)の事後分布の平均値。
- 標準誤差(se_mean): 平均の推定の不確実性を示す。
- 標準偏差(sd): パラメータの事後分布の変動を示す。
- パーセンタイル(10%, 50%, 90%): 事後分布の下位10%、中央値(メディアン)、上位90%の値。
- 有効サンプルサイズ(n_eff): パラメータ推定の精度と信頼性を示す。大きいほど良い。
- Rhat(ゲルマン-ルビン診断): 収束診断の指標。1に近いほど良い。1.01以上は収束していない可能性がある。
HMC診断の解釈
Divergences: 0 of 4000 iterations ended with a divergence. Tree depth: 0 of 4000 iterations saturated the maximum tree depth of 10. Energy: E-BFMI indicated no pathological behavior.
- Divergences: サンプリング中の発散(分岐)の数。0は良好。
- Tree depth: サンプリング時の木の深さ。最大深さまで達していないのは良好。
- Energy: E-BFMI(Bayesian Fraction of Missing Information)の診断。問題がないことを示している。
収束診断プロット
library(bayesplot) # 収束診断のためのプロット
color_scheme_set("brightblue")
mcmc_trace(fit, pars = c("alpha", "beta", "sigma")) # トレースプロット
mcmc_pairs(fit, pars = c("alpha", "beta", "sigma")) # ペアプロット
トレースプロット
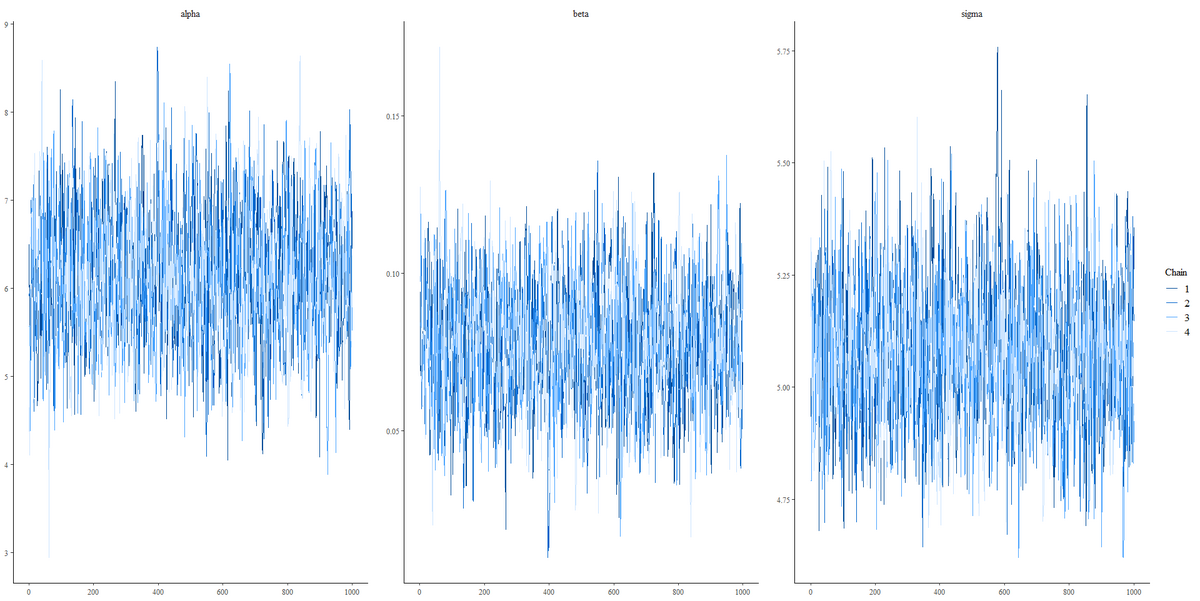
- 混合 (Mixing): 良好な混合は、全てのチェーンがお互いに絡み合い、同じ値の範囲を探索している様子を示すプロットでは、alpha、beta、sigma の全てのチェーンが重なり合い、広い範囲を探索しているのが見て取れ一般的に良好なサインである。
- 定常性 (Stationarity): チェーンが特定の値に偏ることなく、全体として均等に分布している場合、サンプリングが定常状態にあると言える。ここでは、どのパラメーターも定常的に見えるが、alpha と sigma にいくつかの長いトレンドが見えるかもしれない。これは、サンプリングが特定の領域にとどまる傾向を示している可能性がある。ただし、これが問題であるかどうかは、他の診断と組み合わせて評価する必要がある。
- オートコリレーション (Autocorrelation): 各サンプルが互いに独立していれば、プロットはランダムな上下の変動を示す。ここでは、特にbetaに関しては、独立していると考えられるが、alphaとsigmaについては若干の系列相関がある可能性が示唆されている。
- 収束 (Convergence): もし全てのチェーンが同じ分布に収束していれば、異なる色のラインは重なり合って同じパターンを形成する。このプロットでは、チェーンが相互に重なっており、収束している良い兆候を示している。
ペアプロット
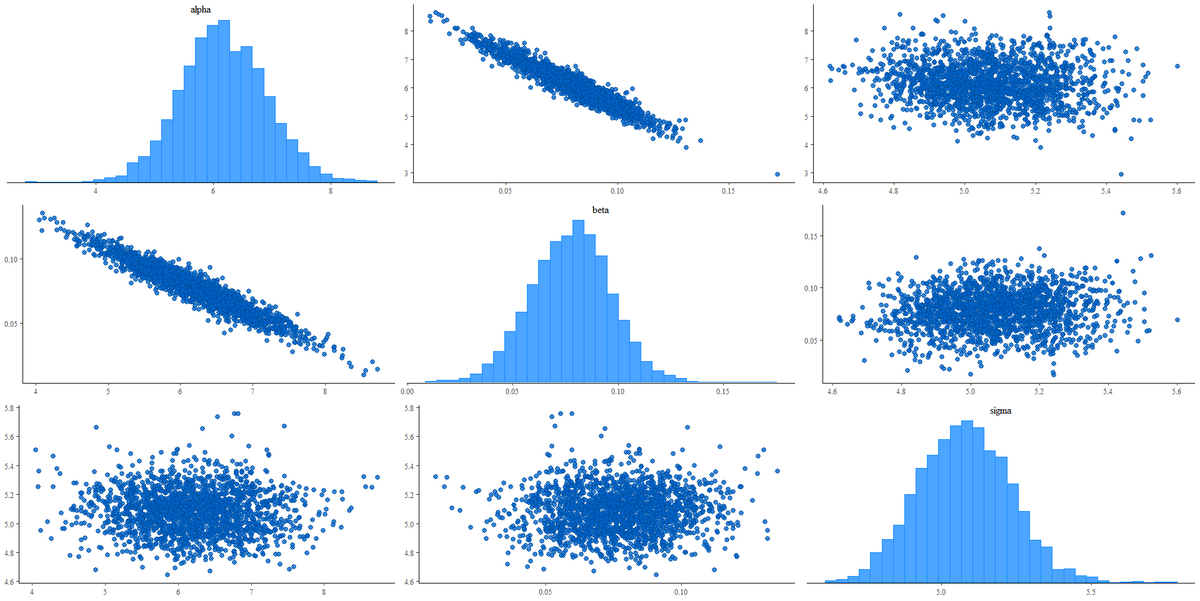
alphaのヒストグラムはほぼ正規分布に近い形をしており、推定値に関する不確実性が対称的であることを示している。betaのヒストグラムもまた、正規分布に似た形状であり、推定値の不確実性が比較的小さいことを示している。sigmaのヒストグラムはやや右に裾野を広げた形をしており、変動の程度が大きいことを表している。
alphaとbetaの散布図は明瞭な負の相関を示しており、alphaの値が大きい場合、betaの値が小さい傾向にあることを示している。これは、切片と傾きが相補的な関係にあることを反映している可能性がある。一方、alphaとsigma、betaとsigmaの散布図は、明瞭な相関関係を示していない。これは、これらのパラメータ間には直接的な依存関係が少ないことを意味している。