https://glmnet.stanford.edu/articles/glmnet.html
はじめに
Glmnetは一般化線形モデルおよび類似モデルをペナルティ付き最尤法でフィッティングするパッケージである。正則化パラメータλの値のグリッド(対数スケール)において、正則化パスがlassoまたはelastic net制約に対して計算さ れる。このアルゴリズムは非常に高速で、入力行列xのスパース性を利用することができる。線形回帰モデル、ロジスティック回帰モデル、多項回帰モデル、ポアソン回帰モデル、Cox回帰モデルに適合します。また、多重応答線形回帰、カスタムfamilyの一般化線形モデル、緩和されたlasso回帰モデルもフィットできる。このパッケージには、予測やプロットのためのメソッド、交差検証のための関数が含まれている。
glmnetの著者は、Jerome Friedman、Trevor Hastie、Rob Tibshirani、Balasubramanian Narasimhan、Kenneth Tay、Noah Simonで、Junyang Qianの貢献もあり、RパッケージはTrevor Hastieが保守している。glmnetのMATLABバージョンはJunyang Qianが、PythonバージョンはB. Balakumarがメンテナンスしている(どちらも数バージョン遅れているが)。
このビネットはRでのglmnetの基本的な使い方を説明している:
"正則化Cox回帰 "は、glmnetを使って生存データに正則化Coxモデルを適合させる方法を記述している。 "glmnetのGLM family functions" は、family引数を通して、elastic netペナルティでカスタム一般化線形モデル(GLM)を適合させる方法を説明している。 「The Relaxed Lasso "では、relax引数を使ったrelaxed lasso回帰モデルの適合方法が説明されている。
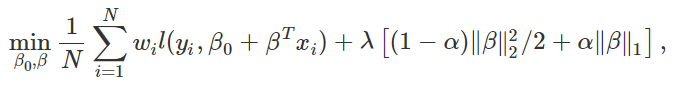
glmnetは、可能な解の全範囲をカバーする の値のグリッド上で問題を解く。ここ[tex: (y{i}, \eta{i}]では観測
例えば、ガウスの場合は
. elastic net制約は
によって制御され,ラッソ回帰(
, デフォルト)とリッジ回帰の間のギャップを埋める。リッジ回帰 (
=0 ). チューニング・パラメータ
は、制約の全体的な強さを制御する。
リッジ制約が相関予測変数の係数をお互いに縮める一方、lassoはそれらの1つを選んで他を捨てる傾向があることが知られている。elastic net 制約は、この2つを混在させる:リッジ制約が相関予測変数の係数をお互いに縮める一方、lassoはそれらの1つを選んで他を捨てる傾向があることが知られている。elastic net 制約は、この2つを混在させる:予測変数がグループで相関している場合、α=0.5は、特徴量のグループ全体を選択または除外する傾向がある。これはより高いレベルのパラメータであり、ユーザーは前もって値を選ぶか、いくつかの異なる値で実験するかもしれない。例えば、のelastic netは、lassoとよく似ているが、極端な相関によって引き起こされる縮退や乱暴な振る舞いを取り除くことができる。
glmnetアルゴリズムは、cyclical coordinate descentを用いており、各パラメータ上の目的関数を他のパラメータを固定したまま逐次最適化し、収束するまで繰り返し循環させる。また、本パッケージは、アクティブセットの効率的な制限のための強い規則を利用する。非常に効率的な更新と、ウォーム・スタートやアクティブ・セット収束などのテクニックにより、我々のアルゴリズムは解のパスを非常に高速に計算することができる。
このコードでは、スパースな入力行列形式や係数の範囲制約を扱うことができる。glmnetのコアはFortranのサブルーチン群であり、非常に高速に実行できる。
この実装の理論とアルゴリズムは、Friedman, Hastie, and Tibshirani (2010), Simon et al. (2011), Tibshirani et al. (2012), Simon, Friedman, and Hastie (2013) に記述されている。
インストール
他の多くのRパッケージと同様、glmnetを入手する最も簡単な方法は、CRANから直接インストールすることである。Rコンソールに以下のコマンドを入力する:
install.packages("glmnet", repos = "https://cran.us.r-project.org")
インストールする場所や好みに応じて、repos引数を変更することができる。パッケージをインストールするディレクトリなど、他の引数もコマンドで変更できる。詳細については、help(install.packages)を参照してください。または、CRANからパッケージ・ソースをダウンロードし、Unixコマンドをタイプして希望の場所にインストールすることもできる。
クイックスタート
このセクションの目的は、ユーザーにパッケージの一般的な感覚を与えることである。主な機能、基本的な操作、出力について簡単に説明する。このセクションの後、ユーザーはどのような関数が利用可能か、どの関数を使うべきか、あるいは少なくともどこに助けを求めればよいかをよりよく理解できるであろう。
まず、glmnetパッケージをロードする:
library(glmnet)
このパッケージで使われるデフォルトのモデルは、ガウス線形モデルまたは "最小二乗法 "であり、このセクションでそれを実証する。説明のためにあらかじめ作成したデータセットをロードする:
data(QuickStartExample) x <- QuickStartExample$x y <- QuickStartExample$y
このコマンドは、保存されたRデータアーカイブから入力行列xと応答ベクトルyをロードする。
glmnetの最も基本的な呼び出しを使ってモデルをフィットさせる。
fit <- glmnet(x, y)
fitはglmnetクラスのオブジェクトで、fitされたモデルの関連情報をすべて含んでいる。我々は、ユーザが直接成分を抽出することを推奨していない。その代わりに、plot、print、coef、predictといったさまざまなメソッドがオブジェクトに用意されており、これらのタスクをよりエレガントに実行することができる。
plot メソッドを実行することで、係数を可視化することができる:plot メソッドを実行することで、係数を可視化することができる:
plot(fit)
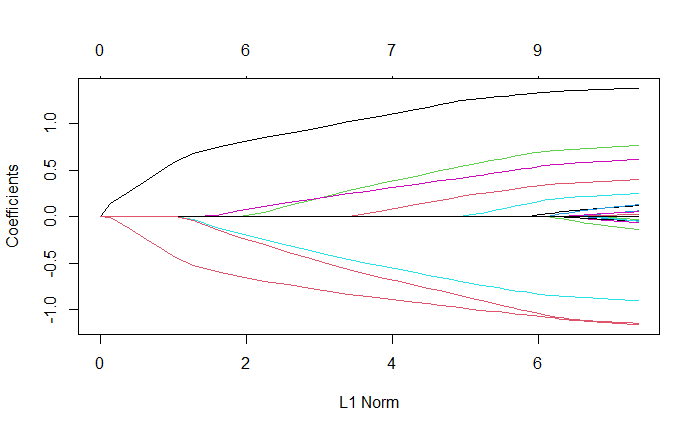
各曲線は変数に対応する。係数ベクトル全体の $l_1-norm$ℓに対する係数の軌跡を示している。の変化に対する係数の軌跡を示している。上の軸は、現在の$\lambda$における非ゼロ係数の数を示しており、これがlassoの有効自由度(df)となる。ユーザーは、曲線に注釈を付けることもできる。これは、plotコマンドでlabel = TRUEを設定することで可能である。
オブジェクト名を入力するか、print機能を使えば、各ステップでのglmnetパスの概要が表示される:
print(fit)
Call: glmnet(x = x, y = y) Df %Dev Lambda 1 0 0.00 1.63100 2 2 5.53 1.48600 3 2 14.59 1.35400 4 2 22.11 1.23400 5 2 28.36 1.12400 6 2 33.54 1.02400 7 4 39.04 0.93320
左から順に、ゼロでない係数の数(Df)、(ヌル値の)偏差を説明した割合(%dev)、$/lambda$(Lambda)を示している。glmnetは、デフォルトでは100個のλの値に対してモデルを適合させるが、%devがある$/lambda$から次の$/lambda$まで十分に変化しない場合(典型的にはパスの終わり付近)、早期に停止される。
モデル係数は、1つ以上の$/lambda$のシーケンスの範囲内でモデル係数を得ることができる:
coef(fit, s = 0.1)
21 x 1 sparse Matrix of class "dgCMatrix"
s1
(Intercept) 0.150928072
V1 1.320597195
V2 .
V3 0.675110234
V4 .
V5 -0.817411518
V6 0.521436671
V7 0.004829335
(なぜλではなくsなのか?将来、他の方法でモデル・サイズを指定できるようにするためである)。ユーザは、新しい入力データで特定のλ で予測を行うこともできる:
set.seed(29) nx <- matrix(rnorm(5 * 20), 5, 20) predict(fit, newx = nx, s = c(0.1, 0.05))
s1 s2 [1,] -4.3067990 -4.5979456 [2,] -4.1244091 -4.3447727 [3,] -0.1133939 -0.1859237 [4,] 3.3458748 3.5270269 [5,] -1.2366422 -1.2772955
関数glmnetは、ユーザが選択できる一連のモデルを返す。多くの場合、ユーザはソフトウェアがその中から1つを選択することを好むかもしれない。cv.glmnetは、プロットや予測などの様々なサポート手法とともに、交差検証を行うためのメイン関数である。
cvfit <- cv.glmnet(x, y)
cv.glmnetは、交差検証適合の全成分を含むリストであるcv.glmnetオブジェクトを返す。glmnetと同様、選択されたλの値を見る以外には、ユーザが直接成分を抽出することは推奨しない。このパッケージは、潜在的なタスクのためによく設計された関数を提供する。例えば、オブジェクトをプロットすることができる:
plot(cvfit)
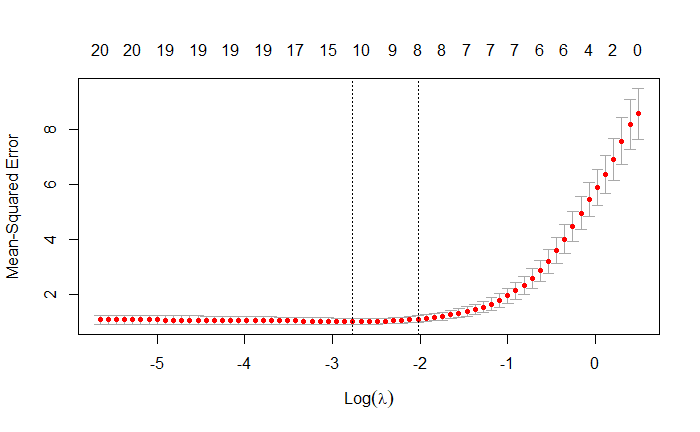
これは、クロスバリデーション曲線(赤い点線)と、λ配列に沿った上下の標準偏差曲線(エラーバー)をプロットしたものである。配列に沿った上下の標準偏差曲線(エラーバー)と共にプロットしている。λ配列に沿った2つの特別な値は縦の点線で示されている。 配列に沿った2つの特別な値を縦の点線で示す。の値で、クロスバリデーションの平均誤差が最小となる。の値であり、クロスバリデーション誤差が最小値の1標準誤差以内に収まるような最も正則化されたモデルを与える。
以下のコードを使って、λ.minの値とその値におけるモデル係数を求めることができる :
cvfit$lambda.min
[1] 0.06284188
coef(cvfit, s = "lambda.min")
21 x 1 sparse Matrix of class "dgCMatrix"
s1
(Intercept) 0.145832036
V1 1.340981414
V2 .
V3 0.708347140
V4 .
V5 -0.848087765
V6 0.554823782
V7 0.038519738
lambda.1seで対応する値を得るには、単に上記のlambda.minをlambda.1seに置き換えるか、lambda.1seがデフォルトなのでs引数を省略すればよい。
係数はスパース行列形式で表現されていることに注意。これは、正則化パスに沿った解がスパースであることが多いため、スパースフォーマットを使用する方が時間的にも空間的にも効率的だからだ。スパースでない形式を使用したい場合は、出力をas.matrix()にパイプを通してほしい。
予測は、フィットされたcv.glmnetオブジェクトに基づいて行うこともできる。以下のコードは、新しい入力行列 newx に対して lambda.min での予測を与えるものである:
predict(cvfit, newx = x[1:5,], s = "lambda.min")
lambda.min [1,] -1.3574653 [2,] 2.5776672 [3,] 0.5846421 [4,] 2.0280562 [5,] 1.5780633
これでglmnet101は終わりである。これまでに紹介したツールで、ユーザーは、リッジ回帰を含むelastic net系列全体を、二乗誤差損失を用いて適合させることができる。このパッケージには、さらに多くの引数があり、ユーザーに大きな柔軟性を与えることができます。もっと学ぶには、後のセクションに進んでほしい。