非標準化推定値と標準化推定値
豊田秀樹『共分散構造分析[R編]』36ページから。
母数の推定値には,非標準化推定値と標準化推定値があります。非標準化推定値は,データを標準化せずに分析を行った際に得られる推定値で,変数の単位の影響を受けます。一方,標準化推定値は,すべての構造変数が標準化された状態で、分析を行って得られた推定値であり,単位の影響を受けません。
「身長(cm)」や「体重(kg)」 といった明確な単位がある場合には非標準化推定値による解釈も可能です,今回の「セミナーデータ」のように構成概念を扱う場合には,非標準化推定値での解釈は難しいです。そのため,論文やレポートでは,標準化推定値を報告します。
リッカート尺度で計測した概念は、標準化した値を使用することようだ。確かにそれぞれの値に意味があるわけではないので、標準化しても問題ないだろうし、分布も正規分布に近似することが多いだろうから、問題はまず起きないだろう。
ちなみに、社会学の回帰分析では標準化した値は使用しない傾向になっているが、変数の単位に意味があったり、2値データがあったりと標準化には向かないためである。
推定される母数は,変数聞の影響関係の程度を表す「係数」と,外生変数の「分散」および「共分散」の2つに大別されます。論文やレポートでは,「係数」の標準化推定値と外生変数間の「共分散(相関)」は最低限掲載するようにしましょう。
係数を論文に書くのは当たり前だが、共分散も掲載する必要があるようだ。その理由は共分散があれば、モデルの計算ができるからだろう。(参照)
概念構成スコア
以前に行った分析を利用する(参照)。
構成概念スコアは、仮説で仮定した構成概念の尺度上で、各観測対象がどの程度その特性を持っているかを表した値のことである。因子分析における因子スコアに相当する。
今回の分析では、dem60(1960年の民主主義)、ind60(1960年の工業化)、dem65(1965年の民主主義)という3つの潜在変数を作成していて、3次の比較になるため、subset関数でdem60とind60を取り出しておこう。
df1 <- predict(object=fit) df2 <- subset(df1, select = c(dem60,ind60)) plot(factor_score, xlab="democracy1960", ylab="industrialized1960")
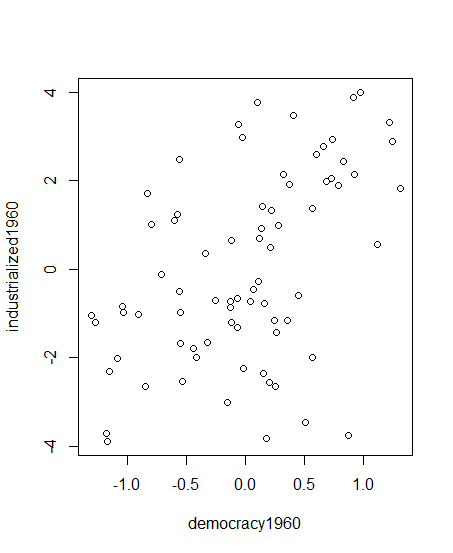
パス図の出力
semPlotパッケージを利用する。
whatLabelsに"stand"を指定すると標準化推定値、optimizeLatResにTRUEを指定すると適切な位置に誤差変数を配置てくれる。
library(semPlot)
semPaths(fit, layout = "tree", whatLabels = "stand",
nDigits=3, shapeMan="square", sizeMan =8,
sizeLat =8, sizeLat2 =8, style = "lisrel",
residScale=12, curve=0.7, optimizeLatRes=T,edge.color="black")
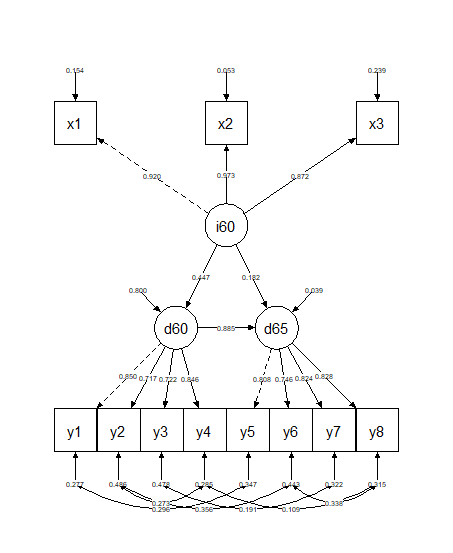
共変量を設定したりすると非常に見にくくなるのが欠点だろうか。
もう少しシンプルなパス図であれば比較的キレイに出力されると思う。
論文に必要な情報
- 構成概念に関する定義
- 観測変数の内容
- パス図
- 観測対象数,観測変数の数
- 推定方法
- ソフトウェア
- 標準化推定値
- 適合度(CFI,RMSEAなど)
- 母数の検定・標準誤差・信頼区間