Mplusの媒介変数(Mediator)の分析。データ欠落については今回はおまけ程度で。
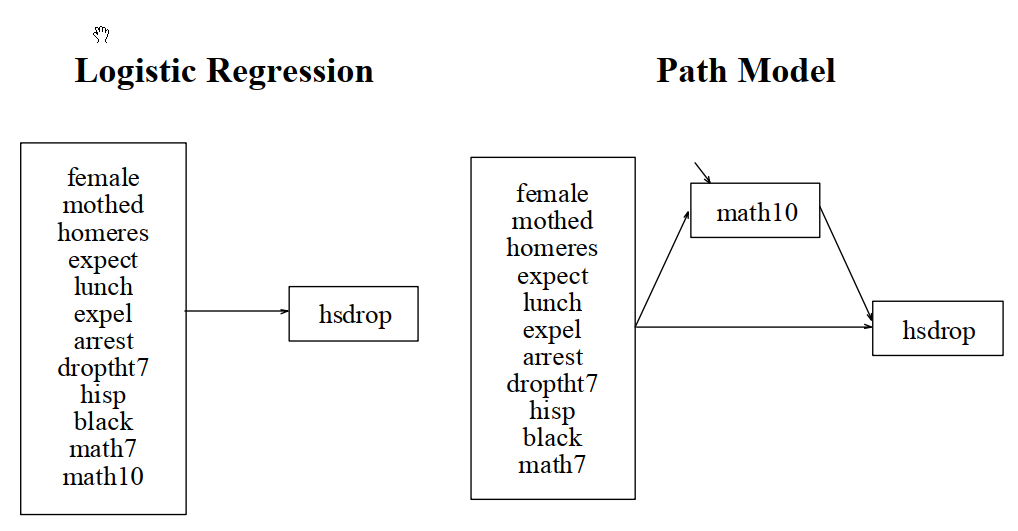
図で一目瞭然だが、ロジスティクス回帰分析(左)に媒介変数が入ったモデル(右)である。
出典はこちら。
https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.367.551&rep=rep1&type=pdf
データ
こちらの"lsaydropout.dat"を使う。 https://www.statmodel.com/mplusbook/chapter9.shtml
コード
PDFにあるコードは微妙にデータと合っていないので修正した。
TITLE: Path analysis with a binary outcome and a continuous
mediator with missing data using Monte Carlo integration
DATA: FILE = lsaydropout.dat;
VARIABLE: NAMES = id female mothed homeres math7 math10 expel arrest
hisp black hsdrop expect lunch droptht7;
USEVARIABLES = female mothed homeres math7 math10 expel arrest
hisp black hsdrop expect lunch droptht7;
MISSING = ALL(9999);
CATEGORICAL = hsdrop;
ANALYSIS: ESTIMATOR = ML;
INTEGRATION = MONTECARLO(500);
MODEL: hsdrop ON female mothed homeres expect math7 math10 lunch
expel arrest droptht7 hisp black;
math10 ON female mothed homeres expect math7
lunch expel arrest droptht7 hisp black;
OUTPUT: PATTERNS STANDARDIZED TECH1 TECH8;
hsdropに回帰させるのは全ての変数。math10が媒介変数なのでmath10以外の全ての変数が回帰されている。媒介変数に回帰させるものだけ選ぶモデルも可能。
例えばmath7だけ媒介変数を通すといったモデルである。
MODEL: hsdrop ON female mothed homeres expect math7 math10 lunch
expel arrest droptht7 hisp black;
math10 ON math7;
モンテカルロ統合をせずに、リストワイズ削除をするのであれば、DATAのところにLISTWISE = ON;と書けばよい。
結果
モデルフィット指標。PDFと結果が違うのでデータも違うのかもしれない。結果はどうでもいいので特に気にしないでおこう。
MODEL FIT INFORMATION
Number of Free Parameters 26
Loglikelihood
H0 Value -4510.967
Information Criteria
Akaike (AIC) 9073.934
Bayesian (BIC) 9210.172
Sample-Size Adjusted BIC 9127.580
(n* = (n + 2) / 24)
モデルの結果。
"HSDROP ON"と書いてある方が最終的なアウトカムになる。この変数が2値である。
"MATH10 ON"と書いてあるのが媒介変数の係数である。
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
HSDROP ON
FEMALE -0.816 0.267 -3.060 0.002
MOTHED 0.037 0.132 0.282 0.778
HOMERES -0.019 0.081 -0.231 0.817
EXPECT 1.127 0.419 2.687 0.007
MATH7 -0.112 0.094 -1.184 0.237
MATH10 -0.029 0.022 -1.284 0.199
LUNCH 1.060 0.408 2.596 0.009
EXPEL -0.033 0.025 -1.325 0.185
ARREST 0.050 0.026 1.945 0.052
DROPTHT7 -0.047 0.396 -0.119 0.905
HISP -0.036 0.020 -1.809 0.070
BLACK 0.016 0.006 2.614 0.009
MATH10 ON
FEMALE 0.887 0.289 3.072 0.002
MOTHED 0.334 0.156 2.133 0.033
HOMERES 0.400 0.099 4.031 0.000
EXPECT 0.753 0.831 0.905 0.365
MATH7 0.024 0.118 0.207 0.836
LUNCH -0.586 0.787 -0.745 0.456
EXPEL 0.458 0.028 16.174 0.000
ARREST 0.142 0.031 4.632 0.000
DROPTHT7 -0.147 0.529 -0.278 0.781
HISP 0.141 0.025 5.701 0.000
BLACK -0.005 0.008 -0.642 0.521
Intercepts
MATH10 6.209 0.893 6.955 0.000
Thresholds
HSDROP$1 0.127 0.763 0.167 0.868
Residual Variances
MATH10 27.441 1.045 26.261 0.000
R二乗値。
R-SQUARE
Observed Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value
HSDROP 0.216 0.042 5.105 0.000
MATH10 0.737 0.012 60.817 0.000
解釈は至って普通。こういう分析を使った分析をみたことがないが、表示は通常の回帰分析と媒介変数を入れたモデルを2列に並べると良いのかもしれない。