今回はRのmclustパッケージで潜在プロファイル分析を行う方法について解説したい。 潜在クラス分析はカテゴリカル変数、潜在プロファイル分析は(基本的には)連続変数という違いはあるものの、ケースごとのパターンからクラス分けをするのは同じである。
使い分けは次のようにするとよい。
潜在クラス分析は2値データの解釈が行いやすいため、基本的には2値データでの使用に留めるのが賢明である。
順序の無い3カテゴリの場合も潜在クラス分析をすることになる。しかし、解釈がややこしくなる。二項ロジスティック回帰分析の解釈が簡単なのに比べて多項ロジスティック回帰分析の解釈がややこしいのと同じである。とはいえ、解釈ができないわけではないので頑張ってクリアカットな結果を出すように頑張るれば使えないわけではない。
もし、順序のついているもの、つまり順序変数であれば、潜在プロファイル分析をした方がよい。
リコードをして潜在クラス分析をしている論文もあるが、潜在プロファイルを使うべきである。
例えば、リッカート尺度で計測したようなものである。「あてはまらない」-「どちらでもない」-「あてはまる」といった、5件法、7件法で計測した質問項目である。
正確に言えば、順序変数と連続変数の水準は異なるのだが、ある程度の順序があれば、連続変数とみなして計算しても、それほど問題は起こらないことがわかっている。シミュレーションによって諸説あるが、だいたい8カテゴリある順序変数であれば、連続変数と同等の結果が得られる。5件法だとさすがに連続変数と同等とはいえないのだが、潜在クラス分析をするためにリコードを行うの方が情報が失われるため、潜在プロファイル分析を行う方が、よほどまし、ということである。
今回取り上げるのはmclustパッケージの開発者たちが書いた論文の例題である。
この例題がこちらのブログで解題されていたので、このブログ記事を参照している。
データ
データは、Kaggle.comで無料で使用できるYoung People Surveyである。
library(tidyverse)
survey <- read_csv("https://raw.githubusercontent.com/whipson/tidytuesday/master/young_people.csv") %>% select(History:Pets)
Young People Surveyはだいたい以下のような感じである。
History Psychology Politics Mathematics Physics Internet PC `Economy Manage… Biology Chemistry Reading Geography `Foreign langua…
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 5 1 3 3 5 3 5 3 3 3 3 5
2 1 3 4 5 2 4 4 5 1 1 4 4 5
3 1 2 1 5 2 4 2 4 1 1 5 2 5
4 4 4 5 4 1 3 1 2 3 3 5 4 4
5 3 2 3 2 2 2 2 2 3 3 5 2 3
6 5 3 4 2 3 4 4 1 4 4 3 3 4
# … with 19 more variables
32の興味/趣味に関する項目が含まれていて、1(関心がない)から5(非常に関心がある)の5段階の順序変数で計測されている。
外れ値を除外する
KaggleによるとSatisficerがいるようである(Satisficerに関してはこちらを参照)。Satisficerとは同じ値を何度も選択した参加者など不適切な回答をしている者である。 carelessパッケージを使用して「文字列応答」(string responding)を識別する。マハラノビス距離で多変量の外れ値を探す。
library(careless) library(psych) interests <- survey %>% mutate(string = longstring(.)) %>% mutate(md = outlier(., plot = FALSE))
最大10に応答する文字列に上限を付け、α=.001のマハラノビス距離をカットオフとして外れ値を除外する。
cutoff <- (qchisq(p = 1 - .001, df = ncol(interests)))
interests_clean <- interests %>%
filter(string <= 10,
md < cutoff) %>%
select(-string, -md)
外れ値を除外した分析データはinterests_cleanの中に格納された状態になっている。
潜在プロファイル分析
潜在プロファイル分析はmclustパッケージを使用して実行する。
library(mclust) interests_clustering <- interests_clean %>% na.omit() %>% mutate_all(list(scale)) BIC <- mclustBIC(interests_clustering)
BICをプロットする。
plot(BIC)
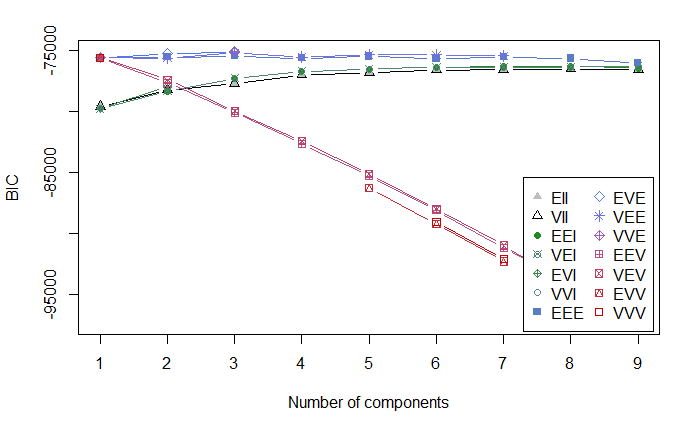
この分析の場合、プロットだけでは、ラインが近接しているので見にくいので、上位3つのBICをsummary()を使って表示させる。
summary(BIC)
下記のように表示される。
Best BIC values:
VVE,3 VEE,3 EVE,3
BIC -75042.7 -75165.1484 -75179.165
BIC diff 0.0 -122.4442 -136.461
最も良好な値を取っているのはVVE,3である。とはいえ、この3つの統計量にそれほどの違いはない。
ガウス共分散行列の各モデルを視覚的に表現すると下記のようになる。こちらの論文に掲載されている図である。
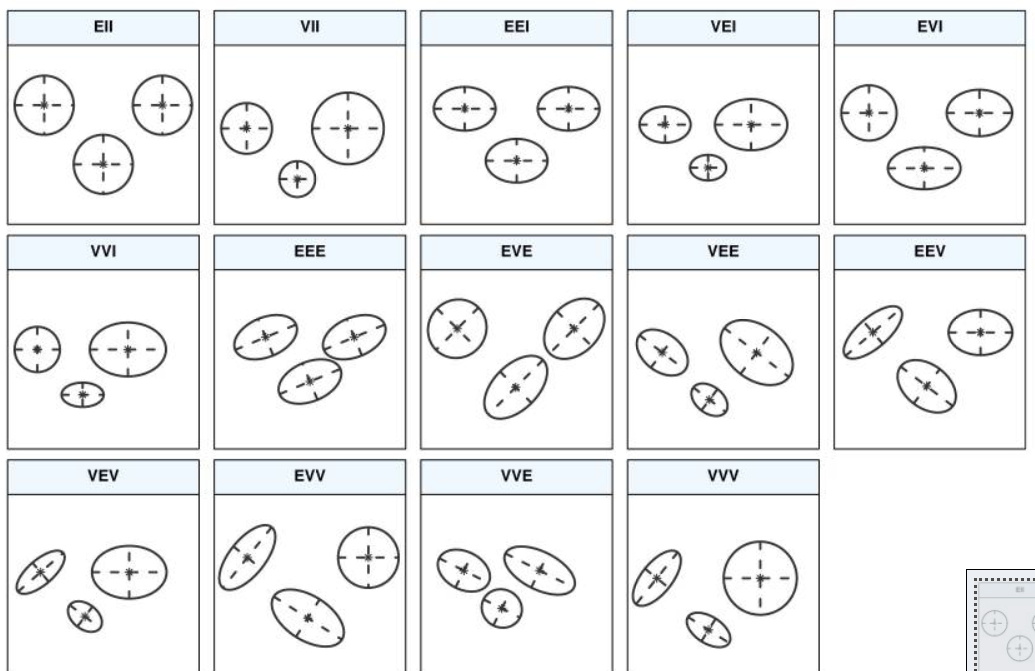
VEE,3は分布の形状が等しくなるように制約をかけているので、実際に分析するのはこのモデルがよいと考えられる。
VEE,3は以下のようなモデルである。
mod1 <- Mclust(interests_clustering, modelNames = "VEE", G = 3, x = BIC) summary(mod1)
結果は以下。
----------------------------------------------------
Gaussian finite mixture model fitted by EM algorithm
----------------------------------------------------
Mclust VEE (ellipsoidal, equal shape and orientation) model with 3 components:
log-likelihood n df BIC ICL
-35455.83 874 628 -75165.15 -75216.14
Clustering table:
1 2 3
137 527 210
これらの統計量単体で適切性は判断できないが、クラスタリングの結果、極端に少ないグループがないことが確認できる。
ICL: Integrated Completed Likelihood (ICL)
BICのほかにICLでもモデルのフィッティングを見る。
ICL <- mclustICL(interests_clustering) plot(ICL) summary(ICL)
結果をプロットすると以下のようになる。
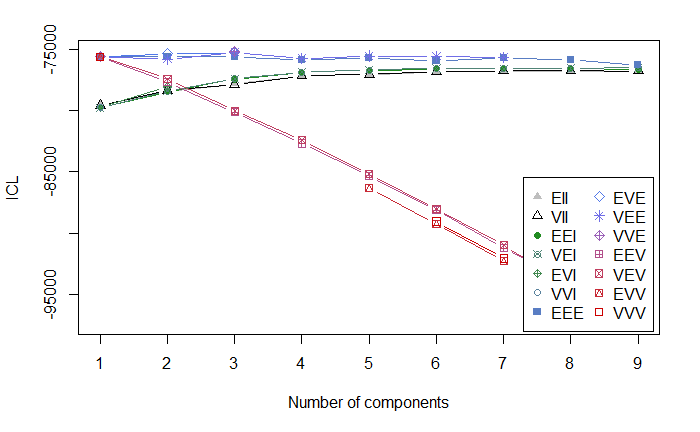
Best ICL values:
VVE,3 VEE,3 EVE,3
ICL -75134.69 -75216.13551 -75272.891
ICL diff 0.00 -81.44795 -138.203
グラフからも、ICLのサマリからも、BICと同じ傾向が確認できる。 ICLで最もフィッティングがよいのはVEE,3である。
以上の分析からVEE,3が最も適切であると判断できる。根拠となるのは以下の3点である。
- 分布の形状が同じになる制約
- BICでVVE,3とほとんど変わらず2番目にフィッティングが良好なモデル
- ICLで最もフィッティングが良好なモデル
BLRT
潜在プロファイル分析でもBLRTを行う。 モデルの選択ではなく、クラス数の選択であり、BICやICLで確認していることとは異なるので注意が必要である。
mclustBootstrapLRT(interests_clustering, modelName = "VEE")
結果は以下。
-------------------------------------------------------------
Bootstrap sequential LRT for the number of mixture components
-------------------------------------------------------------
Model = VEE
Replications = 999
LRTS bootstrap p-value
1 vs 2 197.0384 0.001
2 vs 3 684.8743 0.001
3 vs 4 -124.1935 1.000
3 vs 4でP-Valueが有意ではなくなっており、4クラスモデルで改善が見られなかったということなので、3クラスモデルが良いという提案である。
BIC、ICLはどちらも3クラスモデルを提案していたので、3クラスモデルで間違いなさそうである。
ちなみにBLRTが良いと言っているのは、Mplus開発グループの論文Nylund,Asparouhov, Muthén(2007)である。
https://www.statmodel.com/download/LCA_tech11_nylund_v83.pdf
プロット
各プロファイルの平均値を抽出し、+1 SDを超える値をトリミングする。この作業をしてないとプロットで枠外へはみ出るので必要になる作業である。
library(reshape2)
means <- data.frame(mod1$parameters$mean, stringsAsFactors = FALSE) %>%
rownames_to_column() %>%
rename(Interest = rowname) %>%
melt(id.vars = "Interest", variable.name = "Profile", value.name = "Mean") %>%
mutate(Mean = round(Mean, 2),
Mean = ifelse(Mean > 1, 1, Mean))
ggplot2でプロットを行う。
library(ggplot2)
p1<- means %>%
ggplot(aes(Interest, Mean, group = Profile, color = Profile)) +
geom_point(size = 2.25) +
geom_line(size = 1.25) +
scale_x_discrete(limits = c("Active sport", "Adrenaline sports", "Passive sport",
"Countryside, outdoors", "Gardening", "Cars",
"Art exhibitions", "Dancing", "Musical instruments", "Theatre", "Writing", "Reading",
"Geography", "History", "Law", "Politics", "Psychology", "Religion", "Foreign languages",
"Biology", "Chemistry", "Mathematics", "Medicine", "Physics", "Science and technology",
"Internet", "PC",
"Celebrities", "Economy Management", "Fun with friends", "Shopping", "Pets")) +
labs(x = NULL, y = "Standardized mean interest") +
theme_bw(base_size = 14) +
theme(axis.text.x = element_text(angle = 45, hjust = 1), legend.position = "top")
p1
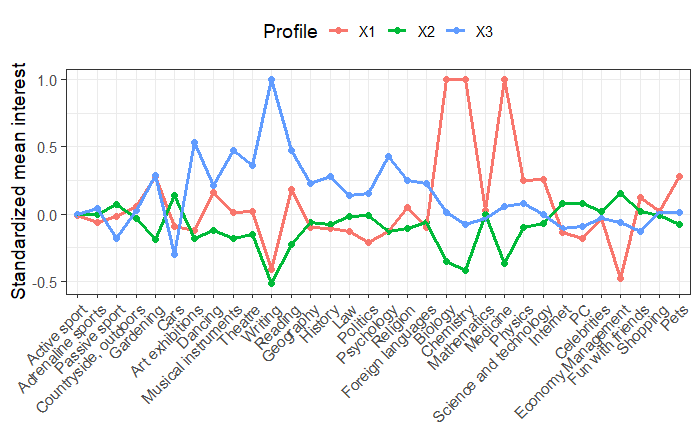
赤のグループは科学に興味があり、青のグループは芸術と人文科学に大きな関心があり、緑のグループは、科学と芸術の両方に関心がないように見えるが、他のことにある程度関心があるように捉えられる。
そこで、1クラスを科学(Science)、2クラスを無関心(Disinterest)、3クラスを人文(Arts & Humanities)とする。
それぞれのクラス名を代入したプロットに書き換える。上のコードとの違いはmutateでクラス名を入れているだけである。
p2 <- means %>%
mutate(Profile = recode(Profile,
X1 = "Science: 16%",
X2 = "Disinterest: 60%",
X3 = "Arts & Humanities: 24%")) %>%
ggplot(aes(Interest, Mean, group = Profile, color = Profile)) +
geom_point(size = 2.25) +
geom_line(size = 1.25) +
scale_x_discrete(limits = c("Active sport", "Adrenaline sports", "Passive sport",
"Countryside, outdoors", "Gardening", "Cars",
"Art exhibitions", "Dancing", "Musical instruments", "Theatre", "Writing", "Reading",
"Geography", "History", "Law", "Politics", "Psychology", "Religion", "Foreign languages",
"Biology", "Chemistry", "Mathematics", "Medicine", "Physics", "Science and technology",
"Internet", "PC",
"Celebrities", "Economy Management", "Fun with friends", "Shopping", "Pets")) +
labs(x = NULL, y = "Standardized mean interest") +
theme_bw(base_size = 14) +
theme(axis.text.x = element_text(angle = 45, hjust = 1), legend.position = "top")
p2
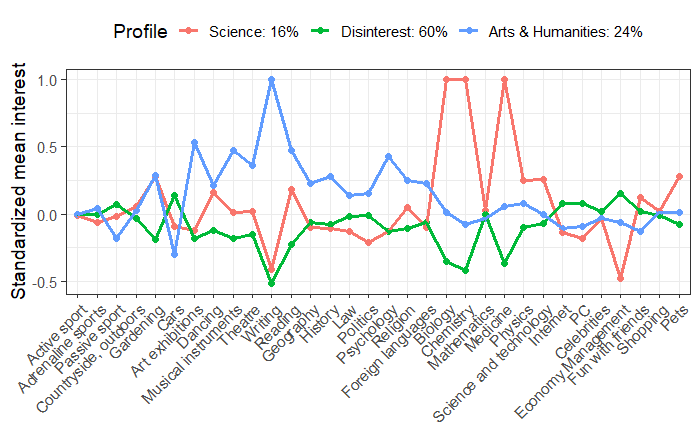
図で確認すると、各クラスの特徴がわかりやすくなる。
いろいろと傾向が読み取れるが、面白いのは、科学(Science)のクラスに属している人は映画館/演劇とセレブに興味がないというのは世情に疎いということだろうか。思い当たる節は確かにある。バリバリの理系の人と話をするときには、芸能話題を選ぼうとは思わない。日本であれば何かのオタクである確率が高い気がする。人文(Arts & Humanities)クラスが経済管理(Economy Management)に興味がない、と出ているが、確かに人文系と経済は相性が悪い。人文系には、経済学的な発想がないというのもあるし、個人的な金銭管理にもあまり興味がないように思う。
余談だが、mclustのブートストラップの反復回数は999回のようである。マシンパワーにもよるが分析は多少時間がかかる。
以前、99について書いたが最近は999ルールなのかもしれない。
追記
このエントリではパイプ演算子を使った書式で書いてある。
パイプが読めないという場合には、下記のエントリに標準書式でのコードを書いておいた。