SEMモデル内に観測されない異質性を組み入れることができる。これを行うために、我々は、観測されない潜在変数を使用する。
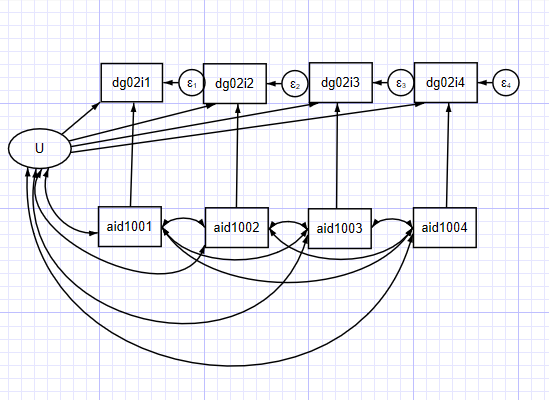
このモデルでは、潜在的なUは独立変数と相関し、従属変数に一定の効果を持つ。
. sem (U -> dg02i1, ) (U -> dg02i2, ) (U -> dg02i3, ) (U -> dg02i4, ) (aid1001 -> dg02i1, ) (aid1002 -> dg02i2, ) (aid1003 -> dg02i3, ) (aid1004 -> dg02i4, ), covstruct(lexogenous, diagonal) cov(lexogenous_oexogenous@0) standardized latent(U ) cov( Uaid1001 Uaid1002 Uaid1003 Uaid1004 aid1001aid1002 aid1002aid1003 aid1003aid1004) nocapslatent
Endogenous variables
Observed: dg02i1 dg02i2 dg02i3 dg02i4
Exogenous variables
Observed: aid1001 aid1002 aid1003 aid1004
Latent: U
Fitting conditional model:
Iteration 0: log likelihood = -3024.3611 (not concave)
Iteration 1: log likelihood = -2790.155 (not concave)
Iteration 2: log likelihood = -2777.439 (not concave)
Iteration 3: log likelihood = -2746.3103
Iteration 4: log likelihood = -2735.1368
Iteration 5: log likelihood = -2701.0888
Iteration 6: log likelihood = -2676.4515
Iteration 7: log likelihood = -2651.019
Iteration 8: log likelihood = -2594.8923
Iteration 9: log likelihood = -2556.8301
Iteration 10: log likelihood = -2548.6717
Iteration 11: log likelihood = -2547.9887
Iteration 12: log likelihood = -2547.9869
Iteration 13: log likelihood = -2547.9869
Fitting target model:
Iteration 0: log likelihood = -2547.9869
Iteration 1: log likelihood = -2547.9869
Structural equation model Number of obs = 140
Estimation method: ml
Log likelihood = -2547.9869
( 1) [dg02i1]U = 1
-------------------------------------------------------------------------------------
| OIM
Standardized | Coefficient std. err. z P>|z| [95% conf. interval]
--------------------+----------------------------------------------------------------
Structural |
dg02i1 |
aid1001 | .0944771 .0248838 3.80 0.000 .0457058 .1432483
U | .9867268 .0087286 113.05 0.000 .969619 1.003835
_cons | 1.78054 .1363356 13.06 0.000 1.513327 2.047752
------------------+----------------------------------------------------------------
dg02i2 |
aid1002 | .0795519 .0238115 3.34 0.001 .0328821 .1262217
U | .9944192 .0076434 130.10 0.000 .9794385 1.0094
_cons | 1.875981 .1410543 13.30 0.000 1.599519 2.152442
------------------+----------------------------------------------------------------
dg02i3 |
aid1003 | .1072014 .0273746 3.92 0.000 .0535481 .1608546
U | .9758766 .0108004 90.36 0.000 .9547082 .997045
_cons | 1.879241 .1417078 13.26 0.000 1.601499 2.156983
------------------+----------------------------------------------------------------
dg02i4 |
aid1004 | .161862 .0319861 5.06 0.000 .0991705 .2245536
U | .9593964 .0161795 59.30 0.000 .9276851 .9911077
_cons | 1.97645 .1467579 13.47 0.000 1.68881 2.26409
--------------------+----------------------------------------------------------------
mean(aid1001)| .3257185 .0867281 3.76 0.000 .1557346 .4957024
mean(aid1002)| .3670659 .0873159 4.20 0.000 .1959299 .5382018
mean(aid1003)| .4761129 .0891765 5.34 0.000 .3013302 .6508955
mean(aid1004)| .3741062 .0874225 4.28 0.000 .2027612 .5454512
--------------------+----------------------------------------------------------------
var(e.dg02i1)| .0316635 .0068772 .0206862 .0484659
var(e.dg02i2)| .0244043 .0061581 .0148826 .0400179
var(e.dg02i3)| .0602049 .0116014 .0412673 .087833
var(e.dg02i4)| .1005082 .017815 .0710112 .1422578
var(aid1001)| 1 . . .
var(aid1002)| 1 . . .
var(aid1003)| 1 . . .
var(aid1004)| 1 . . .
var(U)| 1 . . .
--------------------+----------------------------------------------------------------
cov(aid1001,aid1002)| .8779208 .0193756 45.31 0.000 .8399454 .9158963
cov(aid1001,aid1003)| .618358 .0521995 11.85 0.000 .5160487 .7206672
cov(aid1001,aid1004)| .298639 .0769779 3.88 0.000 .1477651 .4495129
cov(aid1001,U)| -.0762641 .086005 -0.89 0.375 -.2448307 .0923026
cov(aid1002,aid1003)| .650063 .0488007 13.32 0.000 .5544153 .7457107
cov(aid1002,aid1004)| .3680503 .0730669 5.04 0.000 .2248418 .5112587
cov(aid1002,U)| -.1238961 .0852441 -1.45 0.146 -.2909715 .0431793
cov(aid1003,aid1004)| .7115269 .0417278 17.05 0.000 .629742 .7933118
cov(aid1003,U)| -.1148602 .0848663 -1.35 0.176 -.2811951 .0514746
cov(aid1004,U)| -.1518099 .0834334 -1.82 0.069 -.3153363 .0117165
-------------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(10) = 75.37 Prob > chi2 = 0.0000
要約:
- このモデルは、時間とともに変化しない観測されない異質性を表す潜在的なU項を持つ。
- このUは、独立変数と従属変数と相関している。この相関は時間的に一定である。
- 我々は、独立変数からの効果を各時間で一定に設定する。
- また、従属変数の分散も各時刻で一定に設定する。
6.ランダム効果SEM
Random Effect は、U項が独立変数と相関しないことを仮定している。したがって、我々の前のモデルから、それらの共分散を取り除き、REモデルを持つことができる。
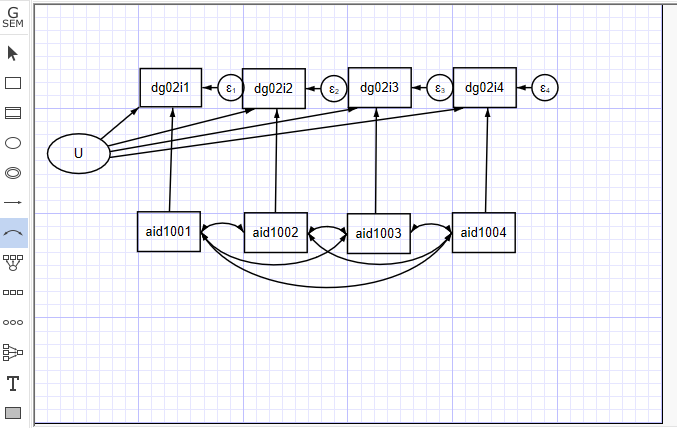
. sem (U -> dg02i1, ) (U -> dg02i2, ) (U -> dg02i3, ) (U -> dg02i4, ) (aid1001 -> dg02i1, ) (aid1002 -> dg02i2, ) (aid1003 -> dg02i3, ) (aid1004 -> dg02i4, ), covstruct(lexogenous, diagonal) cov(lexogenous_oexogenous@0) standardized latent(U ) cov( aid1001aid1002 aid1002aid1003 aid1003aid1001 aid1003aid1004 aid1004aid1001 aid1004*aid1002) nocapslatent
Endogenous variables
Observed: dg02i1 dg02i2 dg02i3 dg02i4
Exogenous variables
Observed: aid1001 aid1002 aid1003 aid1004
Latent: U
Fitting conditional model:
Iteration 0: log likelihood = -3010.3817 (not concave)
Iteration 1: log likelihood = -2784.3438 (not concave)
Iteration 2: log likelihood = -2756.3185 (not concave)
Iteration 3: log likelihood = -2731.7585 (not concave)
Iteration 4: log likelihood = -2722.3319 (not concave)
Iteration 5: log likelihood = -2709.4781 (not concave)
Iteration 6: log likelihood = -2703.332 (not concave)
Iteration 7: log likelihood = -2700.5239 (not concave)
Iteration 8: log likelihood = -2699.3366 (not concave)
Iteration 9: log likelihood = -2698.098 (not concave)
Iteration 10: log likelihood = -2696.6677 (not concave)
Iteration 11: log likelihood = -2693.605 (not concave)
Iteration 12: log likelihood = -2691.2325 (not concave)
Iteration 13: log likelihood = -2689.1527 (not concave)
Iteration 14: log likelihood = -2687.1086 (not concave)
Iteration 15: log likelihood = -2661.4224 (not concave)
Iteration 16: log likelihood = -2641.8011 (not concave)
Iteration 17: log likelihood = -2625.6766 (not concave)
Iteration 18: log likelihood = -2617.3964 (not concave)
Iteration 19: log likelihood = -2589.71 (not concave)
Iteration 20: log likelihood = -2567.8006
Iteration 21: log likelihood = -2557.3664
Iteration 22: log likelihood = -2552.2769
Iteration 23: log likelihood = -2550.3008
Iteration 24: log likelihood = -2550.2726
Iteration 25: log likelihood = -2550.2725
Fitting target model:
Iteration 0: log likelihood = -2550.2725
Iteration 1: log likelihood = -2550.2725
Structural equation model Number of obs = 140
Estimation method: ml
Log likelihood = -2550.2725
( 1) [dg02i1]U = 1
-------------------------------------------------------------------------------------
| OIM
Standardized | Coefficient std. err. z P>|z| [95% conf. interval]
--------------------+----------------------------------------------------------------
Structural |
dg02i1 |
aid1001 | .0889541 .0240784 3.69 0.000 .0417612 .136147
U | .980069 .0042394 231.18 0.000 .97176 .9883781
_cons | 1.771049 .1353193 13.09 0.000 1.505828 2.03627
------------------+----------------------------------------------------------------
dg02i2 |
aid1002 | .0732052 .0228726 3.20 0.001 .0283757 .1180347
U | .9851812 .0036744 268.12 0.000 .9779795 .9923829
_cons | 1.861995 .1400489 13.30 0.000 1.587504 2.136485
------------------+----------------------------------------------------------------
dg02i3 |
aid1003 | .1014453 .0263491 3.85 0.000 .049802 .1530886
U | .9650206 .006648 145.16 0.000 .9519908 .9780504
_cons | 1.861056 .1402512 13.27 0.000 1.586169 2.135944
------------------+----------------------------------------------------------------
dg02i4 |
aid1004 | .1546387 .0303409 5.10 0.000 .0951717 .2141057
U | .9380669 .0107013 87.66 0.000 .9170927 .9590411
_cons | 1.934959 .1430286 13.53 0.000 1.654628 2.21529
--------------------+----------------------------------------------------------------
mean(aid1001)| .3257185 .0867281 3.76 0.000 .1557346 .4957024
mean(aid1002)| .3670659 .0873159 4.20 0.000 .1959299 .5382018
mean(aid1003)| .4761129 .0891765 5.34 0.000 .3013302 .6508955
mean(aid1004)| .3741062 .0874225 4.28 0.000 .2027612 .5454512
--------------------+----------------------------------------------------------------
var(e.dg02i1)| .0315519 .0068498 .0206174 .0482855
var(e.dg02i2)| .024059 .0060736 .0146688 .0394603
var(e.dg02i3)| .0584441 .0113073 .0399997 .0853935
var(e.dg02i4)| .0961174 .0170179 .0679351 .135991
var(aid1001)| 1 . . .
var(aid1002)| 1 . . .
var(aid1003)| 1 . . .
var(aid1004)| 1 . . .
var(U)| 1 . . .
--------------------+----------------------------------------------------------------
cov(aid1001,aid1002)| .8779208 .0193756 45.31 0.000 .8399454 .9158963
cov(aid1001,aid1003)| .618358 .0521995 11.85 0.000 .5160487 .7206672
cov(aid1001,aid1004)| .298639 .0769779 3.88 0.000 .1477651 .4495129
cov(aid1002,aid1003)| .650063 .0488007 13.32 0.000 .5544153 .7457107
cov(aid1002,aid1004)| .3680503 .0730669 5.04 0.000 .2248418 .5112587
cov(aid1003,aid1004)| .7115269 .0417278 17.05 0.000 .629742 .7933118
-------------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(14) = 79.94 Prob > chi2 = 0.0000