Rのlavaanパッケージでパス解析を行う - 井出草平の研究ノート

SEMはMplusを使ってきたので、lavaanパッケージについてはほとんど知らないのだが、使う必要性が出てきたので、勉強がてらにメモ。

いわゆるパス解析をこのエントリーではやってみようと思う。 lavaanパッケージを使用するのでインストールをする。

lavaanパッケージのインストール

install.packages("lavaan")
install.packages("semPlot")

ついでに自動でSEMを描画してくれるsemPlotパッケージもインストールしておく。

サンプルデータとしてAERパッケージに含まれている、CPS1985というデータを使う。下処理として以下のコマンドを走らせておく。

library(lavaan) #lavaanパッケージの読み込み
library(AER)　#AERパッケージの読み込み。
data(CPS1985) #データCPS1985の読み込み

AERパッケージがインストールされていなければインストールする。

変数名と値ラベルを確認しておこう。

データの確認

head(CPS1985)

賃金に対する効果をみたいので賃金("wage")に関係のありそうな、年齢("age"), 性別("gender"), 教育年数("education")の関連をみてみたい。 "gender"は"male"と"female"いう形でデータ化されているので、ダミー変数に変えておく。

ダミー変数に変更する

library(memisc) # memisicパッケージの読み込み。
CPS1985$gender <- recode(CPS1985$gender, "1" <- "male", "2"<-"female")　#リコード
as.factor(CPS1985$gender)　#Factor型への変換

memiscパッケージがインストールされていなければインストールしておく。

1を男性、2を女性にリコードした。このままだと、Rはカテゴリカル変数だと認識してくれないので、as.factor()を使ってFactor型へ変換した。

モデルの構築

model1 <- 'wage ~ age'　# モデル式
fit1 <- sem(model1, data=CPS1985, estimator = "GLS") 　# 分析の実行
summary(fit1, standardized=T,fit.measure=T )　#結果の表示

このモデルは年齢(age)が賃金(wage)に影響を及ぼすというモデルである。ここでやっているのは、単回帰とほぼ同様のことだと捉えて問題ない。

SEMの描画をする。 semPlotライブラリを読み込む。whatLabelsで"est"を指定すると共変量、"std"を指定すると標準化した値を出力する。

library("semPlot")
semPaths (fit1, whatLabels = "est",
layout = "tree", style = "lisrel", nCharNodes = 0, 
sizeMan = 10, edge.label.cex = 2.0)

f:id:iDES:20181118210752p:plain

さて、もう少し複雑なモデルを構築してみよう。賃金(wage)と年齢(age)、性別(gender)、教育年数(education)すべての関連をみるモデルである。

モデルはクォーテーションで前後を囲うのが決まりである。また、一つの従属変数に対しての式を1行で書いて、別の従属変数への効果をみる際には、改行をする。カテゴリカル変数が含まれているので、ロバスト最尤法(MLR)に推定法を変更する。

model2 <- 'wage ~ age + gender + education
               age ~ gender + education
               education ~ gender'
fit2 <- sem(model2, data=CPS1985,estimator = "MLR")
summary(fit2, standardized=T,fit.measure=T )

共変量の部分は以下のような結果となる。

Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  wage ~                                                                
    age               0.113    0.018    6.310    0.000    0.113    0.258
    gender           -2.335    0.392   -5.953    0.000   -2.335   -0.227
    education         0.827    0.080   10.283    0.000    0.827    0.421
  age ~                                                                 
    gender            1.869    1.006    1.858    0.063    1.869    0.079
    education        -0.673    0.209   -3.222    0.001   -0.673   -0.150
  education ~                                                           
    gender            0.011    0.224    0.047    0.962    0.011    0.002

"age"と"gender"、"education"と"gender"は関連がないようである。関連の無いパスは取り除いたてモデルを作成し、それをfit3に格納し、それを描画したのが以下の図である。

semPaths (fit3, whatLabels = "est",
layout = "tree", style = "lisrel", nCharNodes = 0, 
sizeMan = 10, edge.label.cex = 2.0)

f:id:iDES:20181118213947p:plain

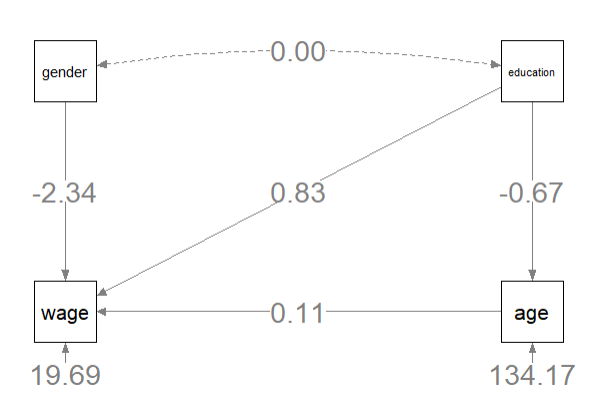
重回帰分析の結果も見ておこう。

lm <- lm(wage ~ age + factor(gender) + education , data=CPS1985)
summary(lm)

結果は以下のようになる。

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -4.84275    1.24425  -3.892 0.000112 ***
age           0.11310    0.01669   6.775 3.32e-11 ***
genderfemale -2.33542    0.38807  -6.018 3.30e-09 ***
education     0.82744    0.07462  11.089  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1```

今回は重回帰とSEMの結果に違いはなかった。 SEMにすることによって、有意でなくなるパスがあるなど場合に、SEMにする価値が生まれる。したがって、今回はSEMを使う意義はあまりないことがわかる。

もう一つのSEM(パス解析)の使い道は、多重共線性があった場合である。多重共線性がある場合には、多重共線性を示す変数を取り除くことになるが、どうしても変数を取り除きたくないといった場合には、SEMが一つの解決策となるだろう。

多重共線性のチェックの指標として使われているのはVIFである。carパッケージが簡単に計算できる。

library(car)
vif(lm)

      age    gender education 
 1.029679  1.006509  1.023228

多重共線性の指標であるVIFは2ないし5以上の値をとると多重共線性があると判断するといわれることが多いが、実際のところ基準というのはあってないようなものである。独立変数に関連が高い変数があった場合に、どちらかを入れた時と、入れなかった時、他方を入れた場合の推定をして、標準誤差や推定値が不安定であるなどなければ、VIFはが高くても特に問題はない。VIFの統計量は一つの参考資料ととらえるのがおそらく正しい。

今回の分析の場合、VIFの統計量をみても、SEMで独立変数間の関連を含めた推定モデルをみても、重回帰での推定結果と大差がないので、重回帰が最適な分析法になると言っていいだろう。