柳井晴夫「因子分析法の利用をめぐる問題点を中心にして」
因子分析について少し勉強をしているところである。因子分析は心理学の人が使うことが多く、心理学徒ではない僕は因子分析をほとんど使ったことがなく、勉強もろくにしたことがないので自分の勉強を兼ねてのエントリーである。
今日、取り上げるのは下記の文献である。
柳井晴夫「因子分析法の利用をめぐる問題点を中心にして」 教育心理学年報 39(0), 96-108, 2000 https://ci.nii.ac.jp/naid/130004572326
この論文は1998年から1999年にかけて教育心理学研究や心理学研究に掲載された論文や学会大会の発表抄録に掲載された論文を対象にしている。それらの論文で、因子分析が適切に使われているかなどを調査している。技法の使用頻度をまとめたのか以下の表である。

1965年からの論文の間違いをチェックしたわけではないようだが、過去1年間の論文について柳井は次のように述べている。
因子分析の主因子法,または主成分分析の結果をバリマックス回転して得られた因子負荷量の平方和を固有値と記述してある論文が最近1年間に発行された教育心理学研究の4論文と心理学研究の1論文に見られた。これは明白な誤りであるが,この誤りは,ここ10年来跡を絶たない。
この誤用パターンはあるあるネタかもしれない。 歴史的に主因子法・主成分分析が使われてきたことが原因なのだろうが、SPSSの推定法の初期値?が主成分分析になっているのも関係しているかもと思ったりもする。
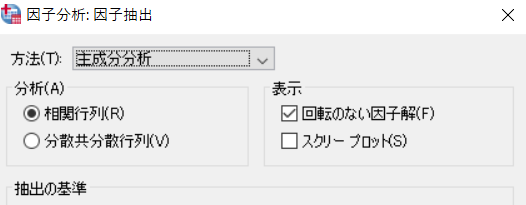
推定方法
因子分析にかける変数を規定する因子があらかじめ仮定されていたり,変数間の相関関係をできる限り少数の因子で説明したい場合には,主成分分析でなく,因子分析モデルを仮定した因子の推定法を適用すべきである。こういった場合の因子負荷量の推定法としては,これまで主因子法が多く使われてきたが,SASやSPSSといったソフトウェアが利用可能な場合には,最小二乗法,重みつき最小二乗法,最尤法などをもっと利用し,可能であれば,異なった手法の適用が分析結果にどのような相違をもたらすかについて考察してほしい。
データの特性を把握して、可能性のある推定法を一通り行うのは当たり前のことだが、意外にそうでもないようだ。現在だと主因子法+プロマックス回転を何も考えず採用している論文が多そうだが、それが正しいとは限らないということことだろう。
回転
バリマックス回転が多いことが指摘されている。
因子分析を用いたとみられる論文数は19編あった。そのうちバリマックス回転を行った論文は13(66%),斜交回転はプロマックス回転(4)・オブリミン回転(1)・斜交プロクラステス回転(1)であり,いまだにバリマックス回転が主流であることがわかる
最近では、プロマックス回転が使われることが多いように思う。バリマックス回転を使わなくなっているので、ずいぶん改善してきたのではないかと思う。論文ではバリマックス回転が適切ではない研究について具体的に指摘されている。
1997年に因子分析の権威マイケル・ブラウン教授が来日された際,斜交回転の方法としてプロマックス回転法とオブリミン回転のどちらが優れているかという質問をしたことがある。このとき,ブラウン教授はためらわずオブリミン法が優れていると回答し,プロマックス回転法については批判的であったことが印象的であった。
プロマックス回転も批判されている。具体的にマイケル・ブラウンが何を言ったかは知らないが、プロマックス回転が簡便法であるところが問題なのではないかと推測している*1。
標準誤差
2000年でもある程度、標準誤差の算出が試みられており、筆者は因子パターンとの併記が望ましいと述べている。まったくその通りだと思う。現在では手技も発達しているかもしれないので、どの方法をとれば標準誤差が出せるのかを調べてみたい。
信頼性係数
(何も考えず)クロンバッハのαを使うことへの批判である。
質問紙による尺度構成の手順としては,因子分析(回転を含む)により抽出された各因子に高い負荷量を有する項目をまとめてα係数を算出するという手続きがかなり定着しているが,村石・豊田(1998)は,尺度に含まれる項目のτ等価(項目得点が真値を共有している)や平行性(τ等価に加えて,誤差分散も等しい)を無視してα 係数を求めることは,必ずしも好ましくないことを警告し,因子負荷量を用いた精密な計算式の利用を推奨している。一方,高木・柳井(1998)はα 係数と同時にθ係数を求め,ある特定の尺度のなかに他の項目と比較してきわめて因子負荷の低い項目が含まれている場合には,θ 係数はα 係数に比べ0.2~0.4増加する事例を報告している。
感想
柳井論文は2000年に公刊されており、1999年までに執筆された論文が対象となっているので今から20年前ほど前の状況が描かれてある。心理学の論文はほとんど読まないので、的外れかもしれないが、争点となるトピックは違っても、同じようなことが起こっている気がする。
僕が最初に因子分析というものを統計パッケージで走らせたのは、大学の3年(だったと思う)の演習授業である。2003年のことだ。担当教員は林直保子先生で、その時に最尤法や最小二乗法を習った記憶がある。バリマックス回転も習ったが、ほとんどのケースではプロマックス回転がいいと習ったように思う。学生に教えるくらいだから、研究者はそのくらいはしていると思い込んでいたが、今回論文を読んで、そうでもなかったことがわかった。確かに林直保子先生は新しい技法を取り入れるスタイルなので、学部の演習でできる範囲で最新のもの教えてくれていたのだろうと思う。
最後に、因子分析とは直接的な関係はないが標準化偏回帰係数についての記載があったので引用しておこう。
喜岡・柳井(1997)は上記,および,Newman,T.B.& Browner,W.S.(1991), Greenland,S.etal.(1991)といった計3つの論文の要旨を紹介したあと,心理学や社会学の行動科学においても同様なことがあてはまることを指摘し,重回帰分析を用いる場合,説明変数の尺度の原点や単位が任意でかつ意味が明確でないときには標準偏回帰係数の利用を,原点や単位の意味が明確な場合には偏回帰係数の利用を薦めている。教育心理学研究で用いられる性格尺度・態度尺度が説明変数となる場合は標準偏回帰係数,医学や疫学で用いられる最大血圧値と血清コレステロール値を用いてある疾患の進行度を予測するような研究の場合には偏回帰係数を用いるべきということになる。例えば,最大血圧値を10下げた場合,最大血圧に与えられた偏回帰係数を10倍した分だけ進行度が改善されることになる。いずれにしても,偏回帰係数と標準偏回帰係数のいずれを選択するか,あるいは回帰分析の使用を止めて他の手法を選択するかは,研究目的・データの収集法・研究結果を実際の現場にどのようにフィードバックすべきかといった様々な要因に影響されるものであることを指摘しておこう。その意味で,判別分析,重回帰分析やパス解析,共分散構造分析において変数の単位や意味に無関係に標準偏回帰係数を利用することは慎むべきであるといえよう。
この主張に反対というわけでもないが、社会学の論文では標準化偏回帰係数は使わないことが推奨されている。 推奨と書くとやや誤解があるが、少なくとも英文で刊行される論文では使われていない。
単位・意味といった点では、社会学の論文は回帰式の結果で従属変数の推定値を出すことが目的ではないこと、モデル間の比較をすることが多いので単位を揃える必要がないことなどが理由である。また、推定値標準化というのは平均が0、分散が1となるようにデータを変換することであり、変数が正規分布がに従うことが仮定されている。しかし、社会学の分析では正規分布が仮定できる変数が少ない。柳井が想定するリッカート尺度を中心とした心理学とは大きな違いだろう。正規分布が仮定できないのに無理やり標準化をすると、当然、偏回帰係数が正しく計算できない。
単位・意味だけではなく、変数を標準化していいのかを考えるべき、という主張であれば、賛同ができるが、このままでは賛同できない、といったところだろうか。