DFactorモデルとは、Discrete Factor Modelsのことで、離散値の探索的因子分析のアプローチの一つである。
世の中では順序や離散データに対して当たり前のようにPearsonの相関係数と最尤法で因子分析している論文ばかりだが、大きな間違いの一つである。
アプローチは3つ考えられる。
1. テトラコリック相関係数を用いた探索的因子分析
テトラコリック相関係数、ポリコリック相関係数用いる因子分析である。ただ、いずれも変数には正規分布を仮定しなければならないという制限がある。順序尺度の場合は正規分布しないことの方が多く、名義尺度の場合は線形ですらないため、正規分布を仮定することはできない。「はい/いいえ」の2択のデータを線形で処理している論文も多いが、明らかな間違いである。
また、推定法として最尤法がよく使われるが、最尤法は連続変数で、変数が正規分布していることを前提としているので、こちらの点でも使いづらい。
2. Muthén(1978)のアプローチ
こちらはMplusに実装されている。
- Muthén, B. (1978). Contributions to factor analysis of dichotomous variables. Psychometrika, 43(4), 551–560. https://doi.org/10.1007/BF02293813
理屈では可能なのだが、実際に分析してみると、うまくいった試しがない。うまくいった人もいるのだろうが、個人的には失敗続きである。 こういったことから必要となってくるのが、3つ目の候補であるVermuntらの開発したDFactorモデルである。
離散因子(discrete factor models: DFactor)モデル
従来の因子分析(FA)では、連続的な観測変数は、1つまたは複数の連続的な潜在因子(CFactor)の線形関数として表現される。DFactor分析は,いくつかの点でFAとは異なる。
観測変数は、名目、順序、連続、計数を含む混合尺度タイプが可能である。潜在変数は、連続ではなく、2つ以上の順序づけられたカテゴリ(レベル)を含む離散である。解を解釈可能にするために回転させる必要がない(「回転」の不確定性の問題は、線形モデルに特有のものである。)
さらに、DFactorのクロス集計により、クラスターのセットが定義される。例えば、2つの二項対立のDFactorVとWは,4つの潜在クラス(4つのクラスター)を生み出す。
| W=1 | W=2 | |
|---|---|---|
| V=1 | X = 1 | X = 2 |
| V=2 | X = 3 | X = 4 |
実行
"gss82white.sav"を開く。このデータはLatentGoldのサンプルデータである。RのpoLCAパッケージにあるgss82とも同じデータである。
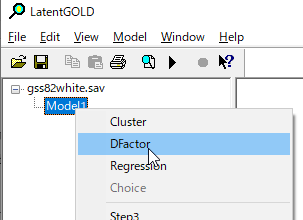
DFactorを選択。
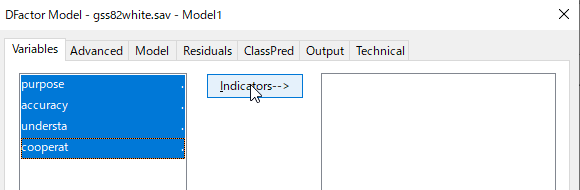
変数を選択肢、Indicatorを押して分析に組み入れる。
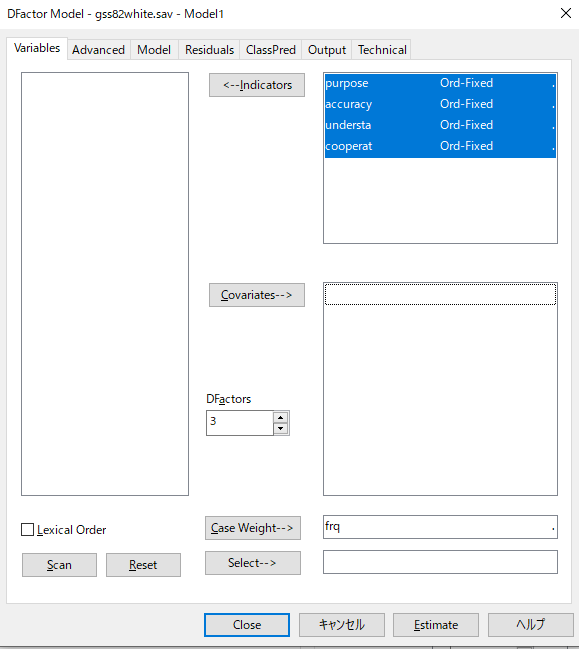
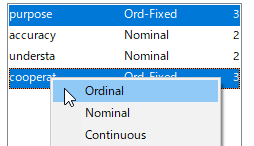
尺度レベルの決定
投入した変数の種類を設定する。
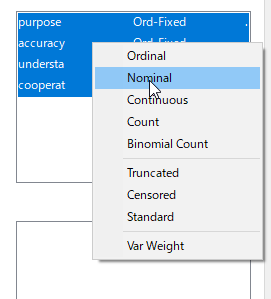
[Nominal]もしくは[Ordinal]を指定する。まずは[Nominal]でやってみよう。
なお、このデータはスタック形式なので、[Case weight]に頻度を入れる。このデータでは頻度が"frq"と名付けられているため、自動的に入るようになっている。
![]()
今回は3因子モデルを実施してみる。
[Estimate]をクリック
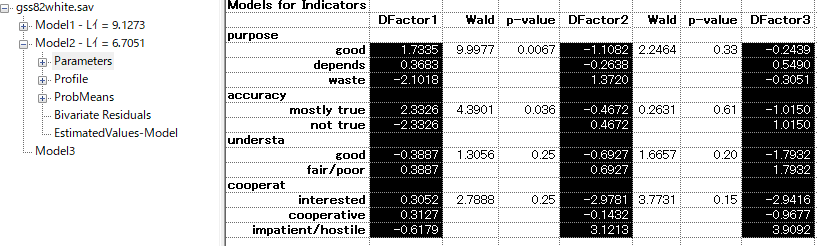
"Parameter"の各Factorの数値をみると、徐々に数値が増加しているパターンのところは順序での推定が良いと考えられる。また、もともと質問文も回答が3値のものは順序として設計されているため、順序での推定の方がよいだろう。
今推定しているモデル図ではModel2をクリックして条件を変えるだけでよい。
因子数の決定
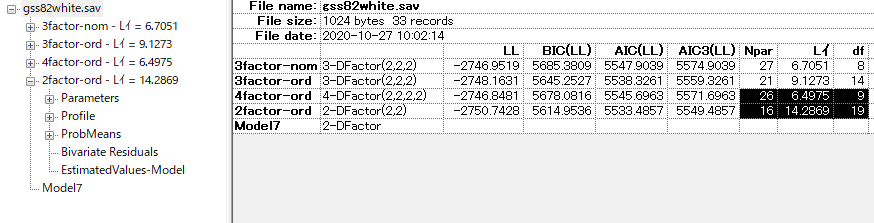
はじめに3因子モデルの推定をやってみたが、他のモデルの推定もしてみよう。
今推定しているモデルをダブルクリックして、Dfactorsを4にして[Estimate]

この画面で書くモデルのAICとBICを比較できる。 DFactorモデルではAICとBICのどちらを優先すれば良いかはよくわからない。潜在クラス分析では一般的にBICを優先することがモンテカルロシミュレーションで示唆されているものの、データの分布次第で変わるため、BICがよいと一概にも言えない。DFactorモデルではおそらく論文が書かれていないはずである。
次に2因子モデルも検討してみよう。
BLRT: Bootstrap Likelihood Ratio Test
特定の分布に依存しない条件付きブートストラップを利用する方法。今回は2因子と3因子を比較するので、3因子モデルで右クリックをして、[Bootstrap -2LL Diff]をクリック

2因子モデルと比較をする。
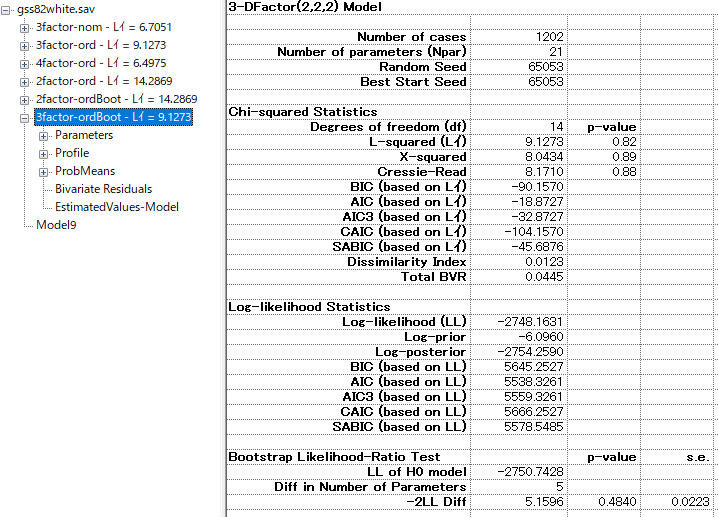
p-valueが5%以下である場合、2因子→3因子でモデルは改善されていると判断できる。この場合は、0.484であるため、2因子モデルが適切ということになる。
VLMR: Vuong-Lo-Mendell-Rubin LIikelihood Ratio Test
[Vuong -2LL Diff]を選択すれはVLMRが可能である。
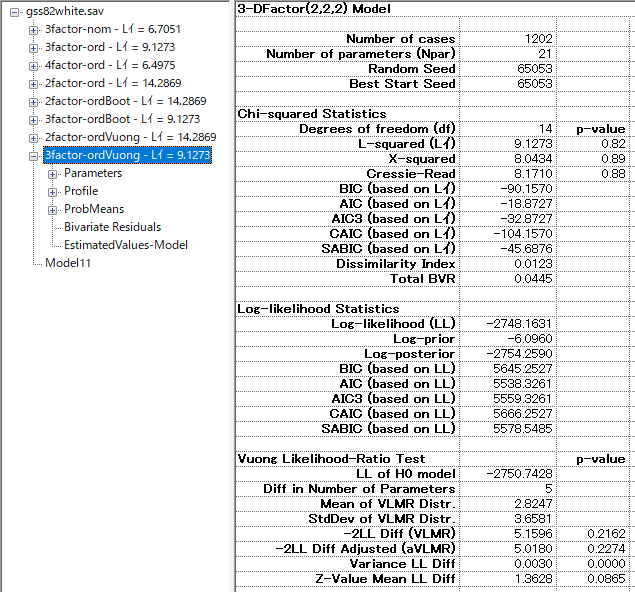
数値は-2LL Diff(VLMR)のところの0.2162か、adjustedの0.2274のどちらかを採用する。どちらがいいのかは情報がないのでよくわからない。おそらくVLMRのところで問題ないだろう。
VLMRでも2因子→3因子でモデル改善はしていないという判断がされた。
因子負荷量
2因子モデルがよいということが分かったので、2因子モデルの因子負荷量をみよう。
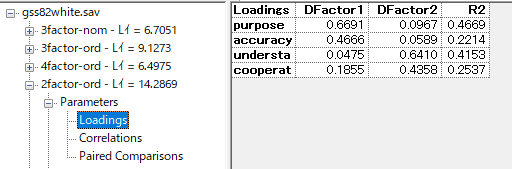
通常の探索的因子分析と同じく、名前をつけるという手順に入る。
文献
Vermunt, J.K., and Magidson, J. (2004). Factor analysis with categorical indicators: a comparison between traditional and latent class approaches. In: Van der Ark, A., Croon, M.A., and Sijtsma, K. (Eds), New Developments in Categorical Data Analysis for the Social and Behavioral Sciences. Erlbaum.
https://www.statisticalinnovations.com/wp-content/uploads/Vermunt2004.pdf
Magidson, J., and Vermunt, J.K. (2003). Comparing latent class factor analysis with traditional factor analysis for datamining. In: Bozdogan, H. (Ed), Statistical Datamining & Knowledge Discovery, Chapter 22, 373-383. Boca Raton: Chapman & Hall/CRC. CRC Press.
https://www.statisticalinnovations.com/wp-content/uploads/Magidson2003.pdf
Magidson, J., and Vermunt, J.K. (2001). Latent class factor and cluster models, bi-plots and related graphical displays. Sociological Methodology, 31, 223-264.
https://www.statisticalinnovations.com/wp-content/uploads/Magidson2001.pdf