二次因子分析モデル(second order factor analysis)とは「斜交解による通常の因子分析の結果,因子聞に強い相闘が観察されたときには,それらの因子に共通して影響を与える上位の因子を想定することができます。このように,通常の因子分析における複数の因子を,さらに少数の因子で説明するモデル」のことである(豊田秀樹『共分散構造分析[R編]』p.56)。
ここではIQの基本的な概念を作成したThurstone & Thurstone (1941)の例を使ってみたい。
Thurstone, L. L., & Thurstone, T. G. (1941), Factorial studies of intelligence https://psycnet.apa.org/record/1941-03743-001
Thurstone & Thurstone (1941)の知能の構造
| Verbal Comprehension, | Word Fluency | Reasoning |
|---|---|---|
| Sentences | First.Letters | Letter.Series |
| Vocabulary | 4.Letter.Words | Pedigrees |
| Sent.Completion | Suffixes | letter.Group |
二次因子分析モデル
下記のようなモデルである。
因子分析モデルではモデルの識別のため以下の3つの方法があり、どれかの方法を選択しなければならない。
- 各構成概念について複数の観測変数あるいは下位の因子に刺さるパス(因子負荷量)のうち任意の1つを1に固定する
- 当該構成概念が外生変数ならばその分散を1に固定する
- 当該構成概念が内生変数ならばその残差の分散を1に固定する
semコマンドのデフォルトは既定値としてパスを1に固定する方法が選ばれる。
引数としてstd.lv=TRUEを入れると、外生変数である2次因子の分散および,内生変数である1次因子の残差分散を1に固定できる。
いずれの制約の置き方でも標準化解は一致する。
データの入力
library(lavaan) VCM <- ' 1 .828 1 .776 .779 1 .439 .493 .46 1 .432 .464 .425 .674 1 .447 .489 .443 .59 .541 1 .447 .432 .401 .381 .402 .288 1 .541 .537 .534 .35 .367 .32 .555 1 .38 .358 .359 .424 .446 .325 .598 .452 1' Thurstone.cov <- getCov(VCM, names = c( "Sentences", "Vocabulary", "Sent.Completion", "First.Letters", "four.Letter.Words","Suffixes", "Letter.Series","Pedigrees", "Letter.Group"))
モデルの作成
model<- 'verbal.Comprehension=~ Sentences + Vocabulary + Sent.Completion
Word.Fluency =~ First.Letters + four.Letter.Words + Suffixes
Reasoning =~ Letter.Series + Pedigrees + Letter.Group
intelligence =~ verbal.Comprehension + Word.Fluency + Reasoning'
分析
fit <- sem(model,
sample.cov = Thurstone.cov, std.lv=TRUE,
sample.nobs = 213)
summary(fit, standardized = TRUE)
結果
lavaan 0.6-6 ended normally after 36 iterations
Estimator ML
Optimization method NLMINB
Number of free parameters 21
Number of observations 213
Model Test User Model:
Test statistic 38.376
Degrees of freedom 24
P-value (Chi-square) 0.032
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
verbal.Comprehension =~
Sentences 0.514 0.063 8.206 0.000 0.903 0.905
Vocabulary 0.519 0.063 8.228 0.000 0.912 0.914
Sent.Completin 0.486 0.061 8.034 0.000 0.854 0.856
Word.Fluency =~
First.Letters 0.520 0.061 8.554 0.000 0.834 0.836
four.Lttr.Wrds 0.496 0.059 8.441 0.000 0.795 0.797
Suffixes 0.437 0.056 7.847 0.000 0.701 0.703
Reasoning =~
Letter.Series 0.451 0.066 6.874 0.000 0.779 0.781
Pedigrees 0.416 0.062 6.729 0.000 0.718 0.720
Letter.Group 0.407 0.061 6.664 0.000 0.702 0.703
intelligence =~
verbl.Cmprhnsn 1.444 0.256 5.641 0.000 0.822 0.822
Word.Fluency 1.254 0.211 5.946 0.000 0.782 0.782
Reasoning 1.407 0.268 5.243 0.000 0.815 0.815
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Sentences 0.181 0.028 6.388 0.000 0.181 0.181
.Vocabulary 0.164 0.028 5.953 0.000 0.164 0.165
.Sent.Completin 0.266 0.033 8.026 0.000 0.266 0.267
.First.Letters 0.300 0.051 5.923 0.000 0.300 0.302
.four.Lttr.Wrds 0.363 0.052 6.941 0.000 0.363 0.365
.Suffixes 0.504 0.059 8.513 0.000 0.504 0.506
.Letter.Series 0.388 0.059 6.594 0.000 0.388 0.390
.Pedigrees 0.479 0.062 7.751 0.000 0.479 0.481
.Letter.Group 0.503 0.063 7.995 0.000 0.503 0.505
.verbl.Cmprhnsn 1.000 0.324 0.324
.Word.Fluency 1.000 0.389 0.389
.Reasoning 1.000 0.336 0.336
intelligence 1.000 1.000 1.000
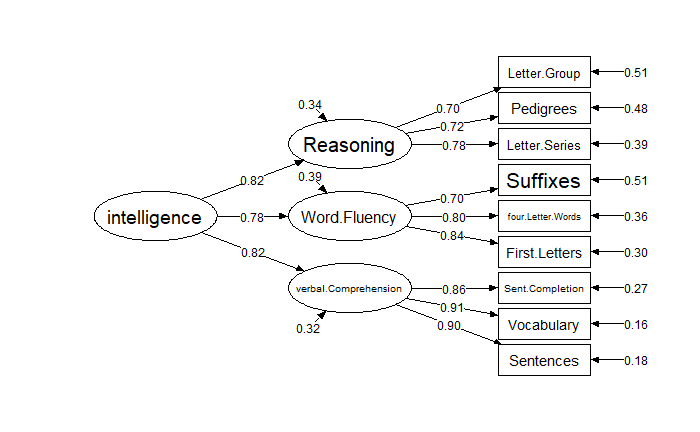
パス図の描画
semPlotパッケージで作図しておこう。
library(semPlot) semPaths(fit,layout="tree",whatLabels="stand", edge.color="black",sizeMan=9, edge.label.cex=0.9, shapeLat="ellipse",sizeLat=15, sizeLat2=8, style="lisrel", optimizeLatRes=T, nCharNodes=0)