歪度と尖度[R]

最尤推定は多変量正規分布に従っているという仮定が置かれているため、最尤推定をするには変数が正規分布に従っているか否かを調べる必要がある。

歪度 skewness

歪度とは、分布がどの程度非対称なのかという指標である。 データPoliticalDemocracyの歪度を計算してみる。

library(lavaan)
library(semTools)
data <- PoliticalDemocracy
lapply(data, skew)

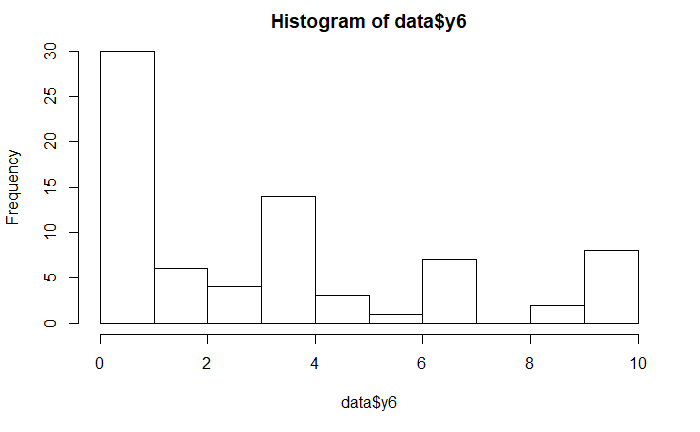
P値も出力され、5%有意であれば、正規分布に従っていないとされる。 y6が有意なので、y6の結果を示す。

hist(data$y6)
skew(data$y6)

歪度は以下。

  skew (g1)          se           z           p 
0.929838580 0.282842712 3.287475827 0.001010899 

歪度の計算はいくつかのパッケージできる。e1071が有名なのではないかと思う。

library(e1071)
skewness(data$y6, type=2)

e1071パッケージでは有意差は出力されないが、3つのタイプの歪度が出力できる。

semToolsパッケージの歪度と一致するのは、type=2で、SASやSPSSで出力される値と同じである。

尖度 kurtosis

正規分布と比べて、尖度が大きければ鋭いピークと長く太い裾をもった分布となる。こちらのページにわかりやすい図があった(参照)

lapply(data,semTools::kurtosis)

こちらも検定結果が有意だと正規分布からの遠くなる。 PoliticalDemocracyデータには有意になるものがないが、y1が比較的P値が少ないためy1を例にとろう。

semTools::kurtosis(data$y1)
hist(data$y1)

尖度は-1.09709367でP値は0.05245193である。

Excess Kur (g2)              se               z               p 
    -1.09709367      0.56568542     -1.93940594      0.05245193 

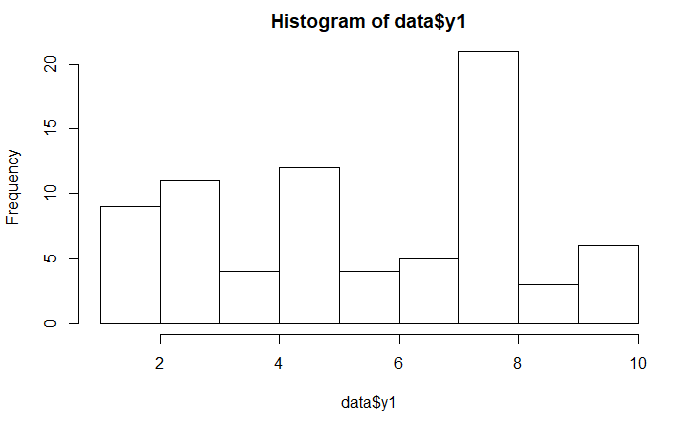
ヒストグラムをみると、分布は比較的なだらかな感じなので、正規分布から離れた分布だと言えよう。

e1071パッケージでも尖度は計算できる。

library(e1071)
e1071::kurtosis(data$y1, type=2)

semToolsパッケージで計算されるのは、e1071パッケージのType2である。これは歪度と同じである。

シミュレーション・データ

分布が正規分布に近いと歪度は0に近づく。 試しに正規分布の乱数を作り、歪度を出してみる。

set.seed(123) 
data2 <- rnorm(10000, mean = 10, sd = 4)
hist(data2)
skew(data2)
semTools::kurtosis(data2)

歪度は0.008200425(P=0.737790343)、尖度は0.01194660(P=0.80734003)となった。
ヒストグラムは正規分布の乱数のシミュレーション・データなので、当然ながら、正規分布に近い形をしている。