Skogによるリーダーマン(S. Ledermann)の単一分布理論に関しての評論。後半1/3の抄訳。
その1はこちら。 ides.hatenablog.com
その2はこちら。
Ledermannの経験的
Ledermannは彼の単一分布理論とともに経験的なデータの分析を発表しました。Ledermannには、これらのデータを用いて、彼の仮説を批判的に検証することが期待されたが、そうはしなかった。対数正規性仮説も分散パラメータに関する仮説も、検証されていない。Ledermannが彼のデータを使っているのは、aの式の中の「定数」Θを推定するためだけである。Ledermannはデータと理論が一致しないのは、理論というよりもデータの弱点の結果として見ていたような印象を受ける。
確かに1956 年に Ledermannが持っていたデータは疑わしいものであった。サンプルの中には非常に小さいものもあれば、特殊な病気を持った人々を中心としたかなり特殊なグループだった。さらに、分布データはかなり粗雑で、いくつかのサンプルでは、アルコール消費のカテゴリー数が非常に少なかった。また、3つの標本では、分布変数はアルコール消費量ではなく、血中アルコール濃度だった。これらのデータを不十分なもので、仮説を裏付けるには難しい。

表からわかるように、経験的に決定された e の値にはかなりのばらつきがある。これらの差が実際にどれほど大きいかを説明するために、年間消費量が20リットルの人口を想像してみよう。e=2.4の値は、ここではa=2.4に対応し、e=4.8はa=0.65に対応する。年間 100 リットル以上の消費量を持つ消費者の割合は、それぞれ3.1%と0.3%となる。Ledermannは自分のデータの中でさえ、eが一定であるという仮説の支持を主張することができなかった。それにもかかわらず、Ledermann は e の「真の」値を推定するために観測された値を使用した。それらが基づいている観察数に応じて発見された値を重み付けすることによって、彼は平均値、e=3.43を得ました。彼はこれを暫定的な推定値として用いています (1956, p. 275)。
分布理論が発表されてから8年後,Ledermannは文献から大量の経験的分布データを収集していた。しかし、彼は、この資料を、分布理論の2つの基本的な仮説である対数正規性仮説とΘが一定であるという仮説の検証に使わなかった。Ledermann (1964a, p. 439-443)は、その代わりに、この理論のおそらく最も重要な帰結、すなわち、平均消費量と重消費者の有病率との関係に焦点を当てている。Ledermann は、これらのデータが推論された仮説を十分に支持すると言うことで、彼の分析を締めくくっている。彼は、平均消費と重度の消費者の有病率との間にはかなり強い関係があり、この関係は理論的なものと非常によく一致していると主張している(Ledermann 1964a, p. 442)。Ledermann の結論の経験的基盤は、図 5 に示されている。
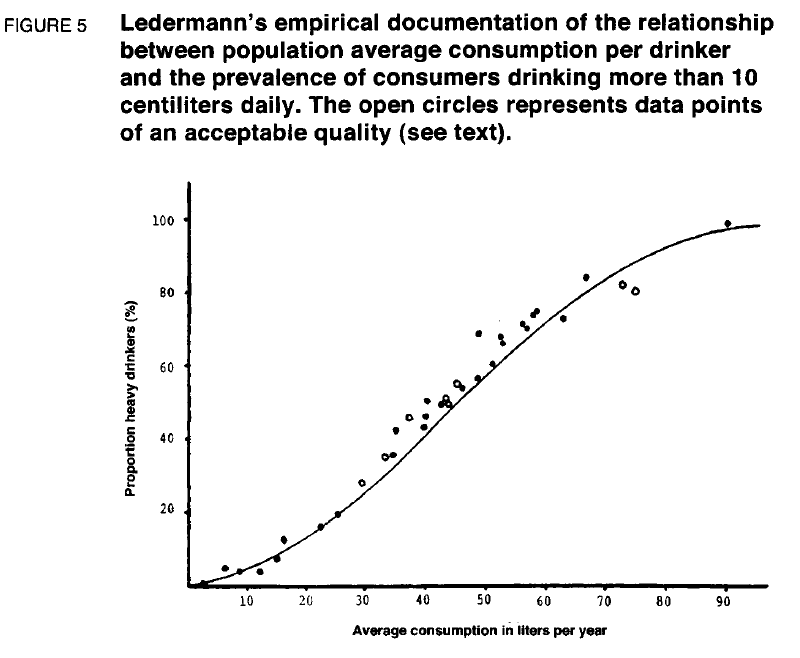
1956年のデータと同様に、新しい資料にも弱点があった。27の標本のうち13は、標本が多様な病気を持つ人々で構成されている疫学研究からとられたものであり、おそらくアルコールが重要な病因となっていると思われる病気であった。このような標本は必然的に飲酒習慣に関しては非典型的であり、集団全体の分布関数と同じタイプの分布関数で記述できる可能性は非常に低い。残りの14の標本は、Ledermannがフランスの様々な地域の消費調査から得たものである(Brezard 1958, 1959, 1960, Brezard & Gombervaux 1962)。他の標本とは対照的に、これらの標本は一般人口から無作為に抽出されたものである。代表されたのは、サンテティエンヌとマルセイユ、そしてジロンド、サヴォワ、ガル、コート・デュ・ノルド、ヴァンデーの特定の農村地域であった。これら7つの標本については、Brezard (1958, 1959, 1960)が女性と同様に男性の消費分布を示しているが、Ledermannは男性標本の分布データのみを利用している。サンテティエンヌの調査では、Brezard (1958) は、6つの異なる社会経済グループの消費分布も示しています。これらのデータもすべて Ledermann が使用している。レデルマンは、ロワールの鉱山労働者を対象とした調査(Brezard & Gombervaux 1962)から得た 14 番目の標本を用いている。
サンテティエンヌの6つのサブサンプルを除いて、これらのデータは人口分布の研究に適しているように思われる。標本は比較的大きく、消費カテゴリーの数も十分であり、最後に、消費の推定値は質が高いと思われる。しかし、サンテティエンヌからの6つの部分標本は、非常に小さく、観測数が14から74の間で変化するので、理想的ではありません。そのため、平均消費量と有病率の両方の推定誤差が大きくなることをが予期される。加えて、2つの推定誤差が強い正の相関を持つ場合、これらの観察の値は限られたものになります。
Ledermann が採用した27の新しいデータセットのうち、最低条件を満たしていると言えるのは8つだけである。残りの19個のサンプルのうち、13個は特定の病気を持っている人だけで構成されているという意味で無関係であり、6個のサンプルは小さすぎて有意な値を持つことができない。8つの適切なサンプルは、図5では白丸で示されている。不十分なデータセットを示す図の点を無視しても、実際には観測された有病率と予測された有病率の間には一定の一致があるように見える。予測がかなり疑わしい前提に基づいていることを考えると、ある明確なずれがあるにもかかわらず、その一致は驚くほど良好であるとさえ言えるかもしにない。有病率と平均消費量の相関も比較的高いようだ。しかし、十分な観測数がないことをを忘れてはいけない。
しかし、平均消費量と重度使用の有病率の関係は同語反復であると主張することができる。平均消費量が低い母集団では、重度使用の有病率は必然的に低く、有病率が高い母集団では、平均消費量は必然的に高くなる。このような背景から、対数正規性仮説も定点仮説も理論的・実証的な根拠に基づくものではないので、有病率の厳密な論理的・生理学的限界に照らし合わせて、Ledermannモデルにおける一人当たり消費量と重度消費者の有病率の予測関係を見ることは興味深いかもしれない。ある平均的な消費について、重度消費者の有病率に理論的にどの程度の変動があると予想できるだろうか。
重消費を定義する限度として、純アルコールを1日10センチリットル、年間36.5リットルとする。平均消費量がこのレベル以下である限り、重消費者の数には上限が存在する。例えば、平均消費量が
年間10リットルの消費者がいる場合、人口の27.4%以上がこの定義上の限界を超えることは不可能である。一般的に、マルコフの不等式から、限界 X^ 以上の消費者の割合がm/X^ より小さくなければならない。これは、mがX^* より小さいときの上限を定義している。mがこの限界を超えると、原則として、人口全体が重消費者になる可能性があります。
この純粋に論理的な制限に加えて、生理的な制限もある。これは、上記とは対照的に、重消費者数の下限を定義したものであり、平均消費量が制限値X^ を超える状況で有効である。平均消費量がX^ 以下である限り、重消費者数は常にゼロである可能性がある。これは、例えば、全員が同じくらいの量を飲んでいる場合に当てはまるだろう。しかし、平均消費量がX^ を超えると、消費レベルが非現実的に高くなるため、重消費者の割合は非常に小さくはならない。人が飲める量には生理的な限界があるので、mがX^ を超えたときの重消費者の割合にも下限が存在する。
Gが生理的限界を表すならば、この下限は(m-X^)/(G-X^)であることが実証される。
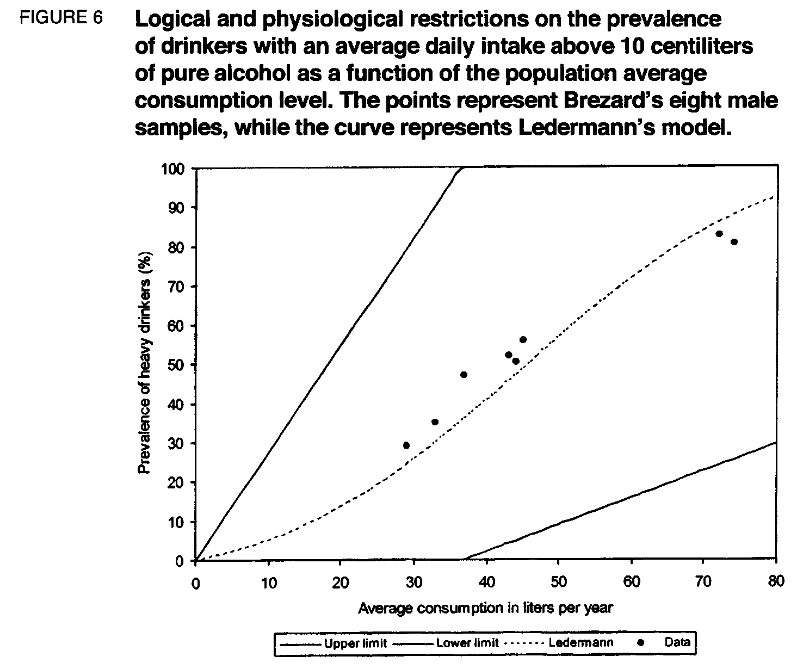
一連の実証研究は、確立されたアルコールの重消費者であっても、1日に40または50cL以上の純アルコールを代謝することができないという方向性を示している(文献の調査については、Lelbach 1974)。これに合わせて、G=年間182.5リットルとした。2つの制限要因は、平均消費量と大消費者(ここでは1日に10cL以上の純アルコールを飲むと定義)の割合との関係の図の中の実現不可能な領域の形で、図6に示されている。純粋に論理的で生理的な重消費者の有病率に対する制限は、あまり強くはない。
見てきたようにLedermann のモデルは、実際の個体群は、許容地域のほぼ中央に位置すると予測しています。このことはBrezardのデータでも確認されており、実際には有病率の変動の潜在的な幅のごく一部しか観察されていないことが示されている。この観点から見ると、人口の平均消費量と重度消費者の有病率との関連性に関するLedermannの予測は、驚くほど良いものであるとさえ言えるかもしれない。理論的には、この関係は全く違った性格のものであったかもしれない。例えば、宿命仮説によって予測されるものと類似している(図4参照)。
まとめ
Ledermannの単一分布理論の先行調査をまとめると、以下のようになる。
Ledermannンは、アルコールの消費者が対数正規分布関数に従って消費規模に沿って分布していると仮定している。これは、個人の飲酒習慣が雪だるま式に、あるいは伝染性のメカニズムによって発展するという前提に基づいている。これらの概念では、明らかにGibratの比例効果の法則を参照しており、社会的相互作用の結果であると主張しているように見える。
Ledermannは、分布の分散パラメータが平均消費量と共分散することで、年間365リットル以上の消費量を持つ人口の理論的な割合が小さく、すべての人口の中で同じであると仮定している。しかし、彼は、なぜこの量が一定でなければならないのかという理由を述べておらず、この仮説は、平均消費量に応じて大消費者の割合が増加するという一つのパラメーターによる分布モデル(one-parametric distribution)を作成するための作為的なものに見える。Ledermannは、死亡者研究に基づいて、仮説の根拠を理由を見つけたようだ。
Ledermannの経験的な研究は、理論を検証するのに適していない弱点のあるものだった。データは、2つの基本的な仮説を説得力を持って支持するものではないが、それにもかかわらず、アルコールの総消費量と人口内の重消費者の有病率との間には関連が存在する可能性があることを示唆している。
Ledermannが自分の仮説を説得力のある理論的議論の上に立証し続けるとは困難である。Gibratの比例効果の法則はもっともらしいと思われるかもしれないが、個人の飲酒習慣が社会的なメカニズムによって大きく規制されているという事実からそれを説明しようとするLedermannの試みは、あまり説得力がない。比例効果の法則は、おそらく全く別の理論的根拠・起源を持っているため、両者はほとんど関連していない。
Ledermannの第二の仮説は、健全な理論的推論に基づいている。Ledermannは365リットル以上の理論的比率がなぜ一定であるべきかについて説明していない。したがって、平均消費量と有病率との関係についての仮説には、実質的な説明がない。Ledermannが平均消費量と死亡率の間で観察した共変動のみに基づいている。しかし、Ledermannの第二の仮説は、厳密に言えば、総消費量と様々なタイプのアルコール関連疾患との共分散の論理的帰結ではないので、この仮説の根拠には問題がないわけではない。線形リスク関数では、平均消費量と重消費者の有病率との間に何の関係もなくても、実際には後者のタイプの関係が存在するかもしれない。
それにもかかわらず、Brezardのデータは、少なくともフランス国内では、平均消費量と重消費者の有病率との間に実際に関連性があることを示している。この関係は確かに完全ではなく、Brezardのデータに基づいて導かれる結論はもちろん限られている。なぜなら、それらはただ一つの飲酒文化を表しているからである。
1960年後半以降、Ledermannの単一分布理論はアングロサクソンと北欧の研究者の間で広く関心を集めた。広範な飲酒文化から得られたデータを利用して、消費分布に関する実証研究が多数発表された。この理論の基本的な仮説は経験的、理論的、両方で吟味されてきた(初期の文献のレビューについては、Bruun et al.1975を参照)。少なくとも第一近似として、経験的消費分布は確かに滑らかであり、対数正規分布に似ていると結論した。さらに、新しいデータは、集団平均消費と大量飲酒者の有病率との間に実際に凸相関があることを確認した。後に、後者の関係を説明する社会的メカニズムが提唱された(Skog 1985)。このメカニズムの本質は、個人間の社会的相互作用、および社会的ネットワークにおける伝染様拡散過程(Skog 1979, 1986)である。これらのメカニズムは、多くの(すべてではない)状況下で、個人の消費レベルにおける協調的なプロセスを作り出し、集団的飲酒文化(Skog 1985)と呼ばれるものを生み出す可能性がある。Ledermannの直観は、少なくともおおよそは正しかったようだが、その前提は疑わしいものだった。
飲酒文化の集団性の理論は、飲酒問題を防ぐことを目的としているならば、厳格な州の規制を支持するために用いられてきた。見落とされがちなのは、同じ理論が、多くの場合、そのような措置の実行可能性はかなり限られていると予測していることである(Skog 1986)。州の規制の有効性は独立した問題であり、他の方法によって評価されなければならない。過去40年間に多数のこのような評価が公表されており、別の箇所でもレビューされている(Edwards et al. 1994、Babor et al. 2003)。